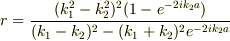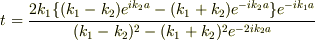線密度が異なった弦の振動
線密度が異なった弦の振動
えり さんの書込 (2008/07/26(Sat) 22:56)
−−−−−=====−−−−− ρ1ρ2ρ1
上図のように左と右の弦の線密度がρ1,中央の線密度がρ2の弦がz=0,z=aでつながっている.
左,中央,右の弦の振動のそれぞれの一般解は
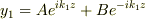
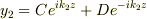
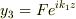 ここで
ここで 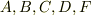 は任意定数.
は任意定数.
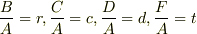 とおく.
境界条件(z=0とz=aでの力と弦の連続性)を考えて,
とおく.
境界条件(z=0とz=aでの力と弦の連続性)を考えて, 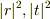 を求めよという問題なのですが,
を求めよという問題なのですが,
解いたら, 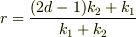
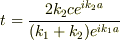 という答えになりました.あまりにも脈絡がない答えなので,不安に思っています.しかもこのrとtを求めたところで何をさせたいのかがいまいちつかめません..
という答えになりました.あまりにも脈絡がない答えなので,不安に思っています.しかもこのrとtを求めたところで何をさせたいのかがいまいちつかめません..
どなたか助言をいただけないでしょうか…よろしくお願いします.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/27(Sun) 01:25)
弦の振動というと,記憶の底にあって朦朧としていますが,ちょっとだけコメントします.
>境界条件(z=0とz=aでの力と弦の連続性)を考えて
これって,y(x,t)と考えた時に,x=0,aに対して;
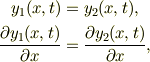
といった境界条件を考えるのでしたっけ?
また,本当の両端は固定されていて,一定の張力で長軸ほうこうに引っ張られていますか?例えば,x=両端のとき
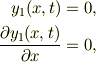
とか.この傾き条件は可笑しいかも.あ,右端の条件は特殊見たいですが,何なのでしょうか?
なお,座標の取り方が非対称的で計算が面倒な気もします.
弦の運動方程式は大丈夫ですよね.
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/27(Sun) 09:00)
一般解の形を見ると, 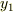 と
と 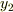 は左右両方向に進む波の重ね合わせであり,
は左右両方向に進む波の重ね合わせであり, 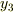 は右向きに進む波を表しています.
従って,左から右に向かって進む波の一部が線密度の不連続点で反射され,残りが右向きに進むわけです.
は右向きに進む波を表しています.
従って,左から右に向かって進む波の一部が線密度の不連続点で反射され,残りが右向きに進むわけです.
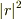 は反射率,
は反射率, 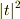 は透過率です.
は透過率です.
なお弦全体は十分に長く,弦の端(での反射)は考えなくてもよいということでしょう.
ところで,波数  を線密度
を線密度  で表しておく必要はないのでしょうか?
また,
で表しておく必要はないのでしょうか?
また, 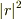 と
と 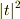 は,最終的にはaを含む式で表されるべきだと思います.
は,最終的にはaを含む式で表されるべきだと思います.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/27(Sun) 11:54)
>従って,左から右に向かって進む波の一部が線密度の不連続点で反射され,残りが右向きに進むわけです.
この点が納得しにくいと感じます.もし,振動体が金属線のようなもので,自立して振動できるとすれば理解出来ますが,弦と言われると外部から張力を加えてやらないと振動する状態にならない,のでは?
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/27(Sun) 12:26)
もちろん張力が加えられていると考えないといけません. 境界条件(z=0とz=aでの力と弦の連続性)も弦全体にわたって一定の張力が加わっていることを示していると思います.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/27(Sun) 12:36)
>弦がz=0,z=aでつながっている.
という事から,線密度が変化する2点の記述であって,左右の端点の説明が不足している様に感じています.
仮に在ったとしても,管楽器のような場合と違って,弦の場合の解放端をイメージ出来ないという意味では,まだ納得できません.
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/27(Sun) 13:41)
現実的には,十分長い弦の両端が固定されていて,固定端から引っ張られているという状況が考えられます. これを理想化して,無限に長い弦に一様な張力が加わっていると考えればいいのではないでしょうか.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/27(Sun) 14:05)
>現実的には,十分長い弦の両端が固定されていて,固定端から引っ張られているという状況が考えられます. >これを理想化して,無限に長い弦に一様な張力が加わっていると考えればいいのではないでしょうか.
そういう解釈ですか.「半直線の弦」というのは始めて拝見しました.確かに電磁気では,無限平面や無限線などを気楽に使っていますから....まるで,「黒線」といった感じですね.
えりさんの問題解説に興味があります.
#もう一度最初のご質問を拝見していたら, #量子力学の壁型ポテンシャルでの反射と透過の問題を連想しました. # #この左端で強制振動を起こし,x=0,a で反射と透過を起こし, #x>aの黒線では透過ばかり,とか.
Re: 線密度が異なった弦の振動
えり さんのレス (2008/07/27(Sun) 14:53)
返信が遅れてすみません. そして,記述不足だったことをお詫びいたします.
この弦は無限の長さであり,両端から一定の張力が加えられており,左の弦に振動源が付いており,左から右へ振動が伝わっていくというモデルです.
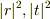 がそれぞれ反射率,透過率を表しているのは理解できました.入射波のAを基準に決めているということですよね?逆に言うと,
がそれぞれ反射率,透過率を表しているのは理解できました.入射波のAを基準に決めているということですよね?逆に言うと,
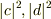 をあえて言葉で表すと,
をあえて言葉で表すと, 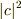 は異なる線密度に入射したときの振幅の増加率,
は異なる線密度に入射したときの振幅の増加率, 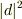 は左の弦での振動を基準とした反射率,といったところでしょうか….
は左の弦での振動を基準とした反射率,といったところでしょうか….
それと,反射率と透過率の和は1でなければならないと思うのですが,どうなのでしょうか?少なくとも私が出した答えでは,足しても1になりそうもないです..
>yamaさん
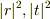 は最終的にaを含む形にしたほうがよいとのご指摘についてですが,
は最終的にaを含む形にしたほうがよいとのご指摘についてですが,  を求める際に,aは消えてしまうように思えます.どのように表現したらよいのでしょうか?
また,波数を線密度に直せという指示はありませんが,別のところの解説で,反射率,透過率が線密度を用いて表されていました.反射率,透過率は線密度で記述されるのが普通なのでしょうか?
を求める際に,aは消えてしまうように思えます.どのように表現したらよいのでしょうか?
また,波数を線密度に直せという指示はありませんが,別のところの解説で,反射率,透過率が線密度を用いて表されていました.反射率,透過率は線密度で記述されるのが普通なのでしょうか?
Re: 線密度が異なった弦の振動
スチーム さんのレス (2008/07/27(Sun) 15:06)
>反射率と透過率の和は1でなければならないと思うのですが,どうなのでしょうか?少なくとも私が出した答えでは,足しても1になりそうもないです..
c,dを決定しないと,解いたことになっていません. 境界条件から,決定してください.そうすればaが入るはずです.
Re: 線密度が異なった弦の振動
えり さんのレス (2008/07/27(Sun) 15:17)
>スチームさん 貴重なお言葉ありがとうございます. 解いてみます.
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/27(Sun) 15:52)
反射率や透過率は,本問の場合は線密度で表したほうがいいのではないかと思ったのですが,一般的には波数を用いて表すことも多いと思います.また,屈折率を用いて表すこともあります.
また,  や
や 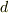 は,計算の便宜上導入された量であって,単にその絶対値が振幅の比であると考えておけばいいと思います.
は,計算の便宜上導入された量であって,単にその絶対値が振幅の比であると考えておけばいいと思います.
なお, 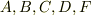 は一般には複素数であることに注意してください.
は一般には複素数であることに注意してください.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/27(Sun) 21:57)
少し前に帰って来て,論議を拝見しています.
初歩的な質問が幾つかあるのでお教え下さい.
(1)左のρ1の左端の強制振動部分は,左方向の無限距離にある?
もしそうなら,少なくとも「左のρ1」は定在波にはなっていないのでしょうか?
(2)時間項が出てこなくても良い理由は?
左端の強制振動の各振動周期で全体の時間応答が規定されるとして, 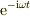 としているのでしょうが.う〜む,考えにくいですね.
としているのでしょうが.う〜む,考えにくいですね.
(3)定常状態になければ,反射と透過の和が1になる保証はありますか?
(4)出来れば,運動方程式,境界条件,強制振動源の表現を教えて戴けませんか?
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/28(Mon) 00:14)
最初の所で,
>左,中央,右の弦の振動のそれぞれの一般解は
> 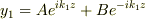 >
> 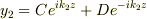 >
> 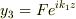 >ここで
>ここで 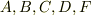 は任意定数.
は任意定数.
としていますが,変位は実数でなければなりませんが,それはどのように確保されるのでしょうか?時間依存性も含めると,更に厄介そうですね.
Re: 線密度が異なった弦の振動
スチーム さんのレス (2008/07/28(Mon) 08:31)
>やはり,の和は1になってくれなそうです..
計算ミスがあります.もう一度,チェックしてみてください. とくにtの分子はもっと簡単な形になり, rの分子の2乗はへんです.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/28(Mon) 09:49)
単純な疑問が止まらないので,教えて下さい.
本問は,線質量密度  の弦に張力
の弦に張力 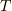 で張った組み合わせの論議です.当然,ある地点,時刻での変位y(z,t)は実数です.変位は運動方程式;
で張った組み合わせの論議です.当然,ある地点,時刻での変位y(z,t)は実数です.変位は運動方程式;
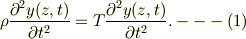
に従います.変数分離で特解をえると,一般解は,右向きの波と左向きの波との合成;
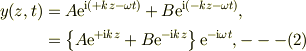
と書けます.
皆さんの方法は,時間要素 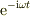 が全て同じだから,「これをすべて括りだして,忘れる」ですが,波の成分バランスを論ずる時には注意が必要な気がします.
が全て同じだから,「これをすべて括りだして,忘れる」ですが,波の成分バランスを論ずる時には注意が必要な気がします.
#むしろ,ある種の時間平均を持ち出して,クロス・タームの時間平均をゼロにするとかの処理がいるように感じます.
式(2)の常数は,
左端の震動源の角振動数: 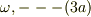 波数:
波数: 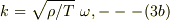 位相速度:
位相速度: 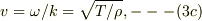 です.
です.
こうしてみると,線質量密度が変わる接続点を境に,波の位相速度も変わる訳です.速度の異なった波の反射・吸収の表現には,別の物理量がいるようにも思えますが...?
以上,解答から離れてしまいましたが,問題が解けた後で結構ですから,解説くだされば幸いです.
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/28(Mon) 10:13)
位相速度の変化は波数の変化の中に繰り込まれていると思います. 本問の定式化では位相速度を直接には扱っていないので,波数の変化以外に位相速度の変化を考慮しなければならない局面はないと思います.
Re: 線密度が異なった弦の振動
MXK さんのレス (2008/07/28(Mon) 11:42)
は実数なので,より正確には,
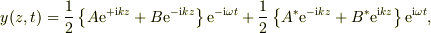
とすべきです. 括弧内を取り出して計算するのは,交流理論などでの常套手段です.必要に応じて元の式に代入すれば,実数量に戻せます.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/28(Mon) 12:40)
> 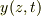 は実数なので,より正確には,
>
>
は実数なので,より正確には,
>
> 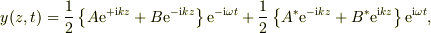 >
>とすべきです.
>
>とすべきです.
正論だと思いますが,そうすると,境界条件で時間項を一律に括りだせなくなりませんか?
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/28(Mon) 13:02)
計算をしないで言うのもおかしな話ですが,中間部ρ2の部分では,右向きの波が左向きの波と同じ大きさでは有りませんよね.有限の差がある分だけここにも流れがあるのでカウントする必要があるのでは?
言い換えれば,「右向きの波の振幅自乗の和」と「左向きの波の振幅自乗の和」が保存するのでは?
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/28(Mon) 14:51)
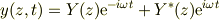
とするとき,例えば任意のtについて境界条件 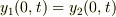 が成り立てば,
が成り立てば, 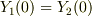 (または同じことですが
(または同じことですが 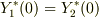 )が成り立つことになります.
つまり時間項を省略することができるわけです.
)が成り立つことになります.
つまり時間項を省略することができるわけです.
>計算をしないで言うのもおかしな話ですが,中間部ρ2の部分では,右向きの波が左向きの波と同じ大きさでは有りませんよね.有限の差がある分だけここにも流れがあるのでカウントする必要があるのでは?
境界条件を満たすように係数を決めることによって,そのような要素も自然に含まれるようになると思います. しかし
>言い換えれば,「右向きの波の振幅自乗の和」と「左向きの波の振幅自乗の和」が保存するのでは?
それが保存しなければならない理由はないと思います.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/28(Mon) 18:35)
yamaさん,
> 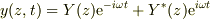 とするとき,例えば任意のtについて境界条件
とするとき,例えば任意のtについて境界条件 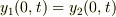 が成り立てば,
が成り立てば, 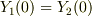 (または同じことですが
(または同じことですが 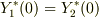 )が成り立つことになります.
>つまり時間項を省略することができるわけです.
)が成り立つことになります.
>つまり時間項を省略することができるわけです.
そうですね,今頃寝ぼけた事を質問してしまいました.強制振動部分が,無限大のところに在って,入射波を作っている違和感から,時間領域の問題に引っかかったようです.ご教示を感謝.
>それが保存しなければならない理由はないと思います.
しかし,入射波,反射波,透過(散乱)波の間で,保存する物理量はあっても良い訳で.運動エネルギ密度,運動量密度などなど.
MXKさん,
>時間平均パワーの計算は
>
> ![\langle y(z,t)y(z,t) \rangle_t =Y(z)Y^*(z)+Y^*(z)Y(z)=2\mathrm{Re}\, \left[Y(z)Y^*(z)\right]](http://hooktail.maxwell.jp/bbslog/ba0ef95b9b6b432fe903124a38ab0d17.png) >
>となります.
>
>となります. 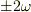 の項は平均操作で消えます.
の項は平均操作で消えます.
ああ,そうですね.意外とお若い方も忘れている可能性が高そうなので,再度引用しておきます.ご教示を感謝.
〜〜〜〜 今更ながらに,私は「弦とか気柱とかの振動」を良く理解していなかったのに気づきました.後は,このスレッドを勉強として拝見させて頂きます.
えりさんの指力に期待します!
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/28(Mon) 21:55)
少し,手をだしてみました.ただし,略記; 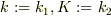
●x=0の境界条件より
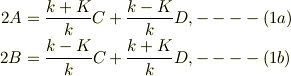
●x=aの境界条件より
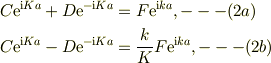
C,Dについて解いて;
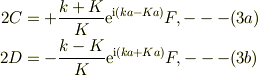
- -> (1)により,C,Dを消去;
![2A = \frac{1}{2kK}\left[ (k+K)^2 \mathrm{e}^{-\mathrm{i}Ka} -(k-K)^2 \mathrm{e}^{+\mathrm{i}Ka} \right]\mathrm{e}^{+\mathrm{i}ka}F, ---(4a)](http://hooktail.maxwell.jp/bbslog/5119b19b419a81c036421f0c2849f27b.png)
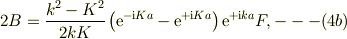
やはりr,tの絶対値の自乗の和は1にならなそうですね.
と書いたら,スチームさんのコメント;
>1になると思います.計算がまちがってないようですけど.
を拝見したので,(4a)を変形して見ましょう;
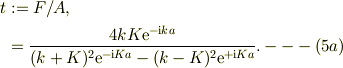
(4a,b)の辺々の比より
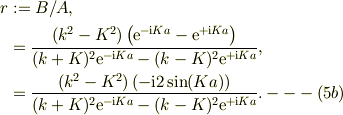
(5)の分母の絶対値の自乗  を計算する
を計算する
![\alpha &:= \left\{ (k+K)^2 \mathrm{e}^{-\mathrm{i}Ka} -(k-K)^2 \mathrm{e}^{+\mathrm{i}Ka} \right\} \left\{ (k+K)^2 \mathrm{e}^{-\mathrm{i}Ka} -(k-K)^2 \mathrm{e}^{+\mathrm{i}Ka} \right\}^* ,\\&= \left\{ (k+K)^2 \mathrm{e}^{-\mathrm{i}Ka} -(k-K)^2 \mathrm{e}^{+\mathrm{i}Ka} \right\} \left\{ (k+K)^2 \mathrm{e}^{+\mathrm{i}Ka} -(k-K)^2 \mathrm{e}^{-\mathrm{i}Ka} \right\} ,\\&= (k+K)^4 +(k-K)^4 -(k+K)^2 (k -K)^2 [ \mathrm{e}^{+\mathrm{i}2Ka} +\mathrm{e}^{-\mathrm{i}2Ka} ]\\&= (k+K)^4 +(k-K)^4 -2(k+K)^2 (k -K)^2 \cos(2Ka),\\&=(k+K)^4 +(k-K)^4 -2(k+K)^2 (k -K)^2 \left( 1-2\sin^2 (Ka) \right),\\&=\left\{(k+K)^2 -(k-K)^2 \right\}^2+4(k+K)^2 (k -K)^2\sin^2 (Ka),\\&= 16k^2K^2 +4(k+K)^2 (k -K)^2\sin^2 (Ka). ---(6)](http://hooktail.maxwell.jp/bbslog/a377cbe965ff4921bccb3411f8eec756.png)
ゆえに
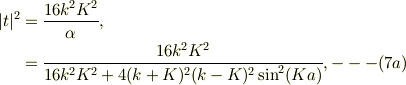
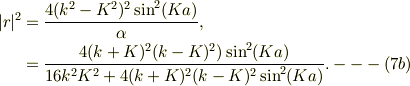
で,どうやら反射と透過で入射になる保存則が成立する様だ.
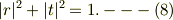
〜〜〜〜 またも三角関数の倍角公式を(6)の所で使用しなかったので,分子同士の和から,逆算できなかった模様.
ところで, 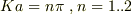 は無反射条件ですが,これは中央部の弦で共振状態にある時の条件と解釈できるのだろうか.ヒョットしてレンズのコーティングの原理なのかも?
は無反射条件ですが,これは中央部の弦で共振状態にある時の条件と解釈できるのだろうか.ヒョットしてレンズのコーティングの原理なのかも?
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/29(Tue) 01:11)
私も計算してみました.
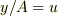 と置くと次のようになります.
と置くと次のようになります.
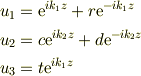
境界条件を用いて次の値が得られました.
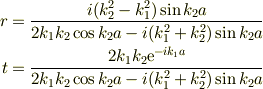
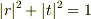 は一応成り立つようですが,もしかすると一部の符号が間違っているかもしれません.
は一応成り立つようですが,もしかすると一部の符号が間違っているかもしれません.
Re: 線密度が異なった弦の振動
MXK さんのレス (2008/07/29(Tue) 08:38)
両端の媒質が等しい場合は,振幅の比の2乗から反射,透過係数は求められます. 等しくない場合は,電磁波のポンティングベクトルに相当するエネルギーの流れで比較しないと, 透過係数が正しく求まらないと思います. 境界が1つの場合もそうです
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/29(Tue) 09:29)
>両端の媒質が等しい場合は,振幅の比の2乗から反射,透過係数は求められます.
まさに実感した気がします.
>等しくない場合は,電磁波のポンティングベクトルに相当するエネルギーの流れで比較しないと, >透過係数が正しく求まらないと思います. >境界が1つの場合もそうです
そういう事ですか.古典力学的な波動でも「エネルギーの流れ」があって良いですよね.これを「classical pointing vector」と命名したりして.あ,天国でクシャミが聞こえた様な....
しかし,そう思ってみると,中間部分の係数C,Dと最後の部分の係数Fとの関係はトリビアルな関係と思っていましたが,媒質の違いが鮮明に出ているという意味で面白いものですね.
Re: 線密度が異なった弦の振動
yama さんのレス (2008/07/29(Tue) 10:00)
密度が変われば,同じ振幅でも単位長さ当たりの運動エネルギーが変化しますし,さらに波の速さが変化することも考慮してエネルギーの流れを計算しなければならないのでしょうね.
ところで,ポインティングベクトルは Poynting vector が正しいようです.
Re: 線密度が異なった弦の振動
mNeji さんのレス (2008/07/29(Tue) 11:44)
>密度が変われば,同じ振幅でも単位長さ当たりの運動エネルギーが変化しますし,さらに波の速さが変化することも考慮してエネルギーの流れを計算しなければならないのでしょうね.
折角,波動の講義も少なからずあるのですから,踏み込んだ解説も有ると良いですね.
その意味では,えりさんのこの問題は,どんな講義ででてきたか知りたくなりました.
>ところで,ポインティングベクトルは Poynting vector が正しいようです.
はは,英語が苦手な私は長いこと,「Poynting vector」を「pointing vector」だとばかり思っていました.で,「エネルギーの流れ」を拝見して,駄洒落を言ってしまいました(笑).