摩擦が与えられた時の運動
摩擦が与えられた時の運動
mNeji さんの書込 (2008/07/26(Sat) 01:22)
以前,kuma(高2)さんが,「運動方程式の合力の向き」というタイトルで,2008/06/22(Sun) 02:05 No.20466の記事で論議をされました.
私は,高校生のころ「摩擦現象」は摩訶不思議な性質であると考えて,自己流の解釈をして,その範囲で解けなければ捨てる,という戦略をとっていました.
ところがkuma(高2)さんのご質問が,私には理解出来なかったので,自分の解釈を; ・2008/06/23(Mon) 15:41 No.20484 ・2008/06/23(Mon) 23:34 No.20490 ・2008/06/24(Tue) 22:43 No.20507 などにお書きしました.
その後,知人との論議で,塾の解説は「コンパクトに纏めた説明」があるようですが,私はその内容を存じません.そこで,下手な解説をして,誤解されるよりは,塾の解説によって理解を深めた方が宜しそうだと思いました.
というのも,一番簡単なケースについて,私は理解出来ない部分があることに思い至ったからです.そこで,自分の疑問をご紹介して,識者の方々からのご意見を戴きたいと思います.
〜〜〜〜
(問題)
水平な平面上に質量mの物体が置かれている.その静止している時の最大静止摩擦係数値を 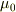 とし,動摩擦係数を
とし,動摩擦係数を 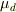 とする.水平面の一点Oを原点とし,そこから右に+x軸を取るとします.物体はt=0まで,原点Oに静止していて,そのご外力Fを+x軸の方向に受けるとします.
(1)外力を増加させた時の運動を論ぜよ.
(2)ある外力
とする.水平面の一点Oを原点とし,そこから右に+x軸を取るとします.物体はt=0まで,原点Oに静止していて,そのご外力Fを+x軸の方向に受けるとします.
(1)外力を増加させた時の運動を論ぜよ.
(2)ある外力 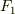 の時に物体が運動しているとして,そこから外力を減少させて行った時に,静止するまでの運動を論ぜよ.
〜〜〜〜〜
の時に物体が運動しているとして,そこから外力を減少させて行った時に,静止するまでの運動を論ぜよ.
〜〜〜〜〜
私は,(1)を解答出来ると思いますが,(2)の静止する時の外力 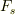 が何なのか判りません.可能性としては,
が何なのか判りません.可能性としては,
[a] 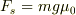 [b]
[b] 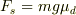 [c]
[c] 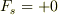
などが有りそうです.
ご説明頂けたら有難いです.
Re: 摩擦が与えられた時の運動
yama さんのレス (2008/07/26(Sat) 08:55)
静止するときの外力は,いろいろな条件によって異なってくると思います. たとえば,外力が急速に減少してほとんど瞬間的に0になった場合は,物体はすぐには静止しないでしばらくは動き続けると思います.
Re: 摩擦が与えられた時の運動
DIO さんのレス (2008/07/26(Sat) 09:06)
Fがある一定値以下を取るからといって急に物体が止まることは無いと思われます.
ですので問題設定として,Fを減少関数として具体的に決めなければ何処で止まるかは分かりません.
しかし条件としては 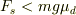 ですよね,合力が正であれば静止し得ないので,
ですよね,合力が正であれば静止し得ないので,
運動方程式から速度について解けば,その 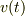 は
は 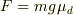 で極大となり,そこからは単調減少,v=0となれば静止します.
で極大となり,そこからは単調減少,v=0となれば静止します.
Re: 摩擦が与えられた時の運動
mNeji さんのレス (2008/07/26(Sat) 10:52)
yamaさん,
>静止するときの外力は,いろいろな条件によって異なってくると思います.
なるほど問題設定が明確ではなかったようですね.では一般的な設問(1)を考えます.この場合,物体の運動方程式を;
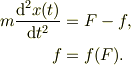
といった連立方程式によって与えると思います.
この時,fは摩擦力で,No.20490で引用した摩擦力の図を図1として再度引用しますと <pre>
摩擦力 f 静摩擦力 ←|→動摩擦力 ↑ |f=F/ |/ |/ |/ |/________f=Mgμ(一定) |/ |/ |/ + ───────・────────────→ |Mgμ_0 外力F
図1静止摩擦力と動摩擦力(出典は数研出版,物理?) </pre>
に従う訳です.
私はこの図を「t=0まで,物体は静止しており,外力もない,その時に外力F=一定が印可された時の運動方程式を与える摩擦力,fの外力Fへの依存性」を示すものと考えました.いわば,外力が「0 →F」と階段関数上に変化した場合の応答を考えていると解釈します.
すると,設問(2)は,物体が十分に大きな外力 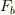 を受けて運動している.ある時刻t=0での速度を
を受けて運動している.ある時刻t=0での速度を 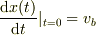 として,外力がt=0を境に,
として,外力がt=0を境に, 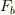 →Fにジャンプした時の運動をどう捉えるか?と考えていました.
→Fにジャンプした時の運動をどう捉えるか?と考えていました.
言い換えると,このような場合,図1に対応する図は別に与えられないといけないのではないか?という疑問です.
DIOさん,
>Fを減少関数として具体的に決めなければ何処で止まるかは分かりません.
先にご説明した様な「 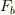 →Fにジャンプ」型の場合,具体的な計算方法をお教え下さると有難いです.
→Fにジャンプ」型の場合,具体的な計算方法をお教え下さると有難いです.
私には,その考え方が判らないので困っているからです.
Re: 摩擦が与えられた時の運動
DIO さんのレス (2008/07/26(Sat) 11:30)
運動→静止を考える際には静止摩擦力係数を考える必要はありません.すなわち,上の図は使う必要がない,ということです.
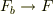 と外力が変化したとき,その後の運動は単に
と外力が変化したとき,その後の運動は単に
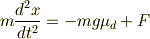
と表せます.
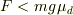 であれば,その後静止します.
であれば,その後静止します.
Re: 摩擦が与えられた時の運動
mNeji さんのレス (2008/07/26(Sat) 11:33)
>運動→静止を考える際には静止摩擦力係数を考える必要はありません.すなわち,上の図は使う必要がない,ということです.
なるほど,一度運動を始めた物体では「動摩擦係数による摩擦力だけにより運動する.」という解釈でしょうか.
上記のご説明の出典をお教え下さると幸いです.
> 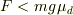 であれば,その後静止します.
であれば,その後静止します.
この点は,まだ理解し切れていません.すこし検討させて頂きます.
Re: 摩擦が与えられた時の運動
DIO さんのレス (2008/07/26(Sat) 12:39)
特に出典は無いのですが, 静止摩擦力は文字通り物体が静止している時に働く力です.物体の速度は連続なので,運動中に動摩擦力→静止摩擦力となれば,その瞬間(運動中)に静止摩擦力が働くことになりこれはおかしいです.よって,動摩擦力→静止摩擦力となるのは,物体が動摩擦力(又は他の外力)によってv=0となった時です.
物体の速度は連続と書いたのですが,少し自信がありません. 外力が区分的に連続な時にそうなると思うのですが,, そうであれば摩擦力が動摩擦力→静止摩擦力と変化するときもこれは区分的に連続なので,上のことがいえます.
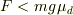 のときは摩擦力を含む外力がマイナスになり,加速度もマイナスになります.
のときは摩擦力を含む外力がマイナスになり,加速度もマイナスになります.
Re: 摩擦が与えられた時の運動
mNeji さんのレス (2008/07/26(Sat) 13:04)
>動摩擦力→静止摩擦力となるのは,物体が動摩擦力(又は他の外力)によってv=0となった時です.
これについては同意します.数学的な問題は,私には判りませんので,コメントができません.
> 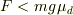 のときは摩擦力を含む外力がマイナスになり,加速度もマイナスになります.
のときは摩擦力を含む外力がマイナスになり,加速度もマイナスになります.
ああ,そうですね.たとえFが正だとしても,速度が正である限り,「力の総和が負になる事」を見逃していました.
確かに(1)タイプでは,正の外力に,負の摩擦力だけど,「総和は正の方向に向く」のが当たり前なのは,初速度=ゼロからの運動なので,初速度の発生は,短時間には
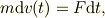
として生ずる為に,外力Fの方向で決まりますが,一般的には動摩擦力の方向は「速度の方向の逆向き」を満たす訳ですね.
どうしても水泳の解析が無意識にあって,速度が表に出てこない固体間の摩擦力の解析には,戸惑います.
あとで,(2)の見解を纏めてみたいと思います.
Re: 摩擦が与えられた時の運動
mNeji さんのレス (2008/07/26(Sat) 21:20)
これまでの纏めを書いて見ます.
〜〜〜〜
問題:
水平な平面上に質量mの物体が置かれている.その静止している時の最大静止摩擦係数値を 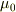 とし,動摩擦係数を
とし,動摩擦係数を 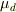 とする.水平面の一点Oを原点とし,そこから右に+x軸を取るとする.物体はt=0まで,原点Oに静止していて,その後に,一定の外力Fが+x軸の方向に加わるとする.
(1)外力を増加させた時の運動(速度,変位)を論ぜよ.
(2)ある外力
とする.水平面の一点Oを原点とし,そこから右に+x軸を取るとする.物体はt=0まで,原点Oに静止していて,その後に,一定の外力Fが+x軸の方向に加わるとする.
(1)外力を増加させた時の運動(速度,変位)を論ぜよ.
(2)ある外力 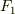 の時に物体が運動しているとして,そこから外力をFに減少させた,
の時に物体が運動しているとして,そこから外力をFに減少させた,  て行った時に,静止するまでの運動を論ぜよ.
〜〜〜〜
解答:
て行った時に,静止するまでの運動を論ぜよ.
〜〜〜〜
解答:
■問い(1)■
物体の運動方程式は;
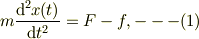
で与えられる.此処で,右辺は,「アモントン-クーロン」摩擦の公式より;
<pre> 外力-摩擦力 F-f静摩擦力領域 ←|→動摩擦力領域 ↑ | / | /F−f_d | /f_d ≡ mgμ_d | / | / | / | | | | | | | | + ─────────・────────────→ | f_0 外力F
≡mgμ_0
図A「外力-摩擦力 vs 外力」「静止摩擦力と動摩擦力(出典は数研出版,物理?)」から改変. </pre>
この図Aの意味は,外力が静止最大摩擦力 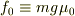 以下である限り,外力に対して静止摩擦力が常にバランスして運動を生じないことを意味する.
以下である限り,外力に対して静止摩擦力が常にバランスして運動を生じないことを意味する.
ところが,外力が 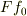 となると正方向の加速を生じるので,運動方程式の逐次積分から,速度,変位を求められる;
となると正方向の加速を生じるので,運動方程式の逐次積分から,速度,変位を求められる;
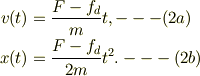
なお,静止状態から外力が加わった時の「摩擦力の方向」を決めるのは「力の方向」によって一意的にきまる.t=0まで外力Fはなく,勿論摩擦力fもない.t=0から時間の微分 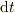 に発生する力積を考えると;
に発生する力積を考えると;
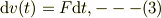
なので,「摩擦力は速度方向の逆に向く」ので(1)に従うことが判る.
■問い(2)■
一度加速を始めた物体は(2)に示したように,正の速度をもって進行している.そこで新たに時間原点0を取り直し,その時の速度 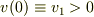 とし,その時の外力
とし,その時の外力 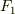 とする.その後,外力を
とする.その後,外力を 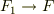 に減少させるとする.
に減少させるとする.
この時の運動方程式;
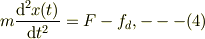
は物体が停止するまで成立する.運動している時の右辺を図Aに類似して描くと
<pre> 外力-摩擦力 F-f静摩擦力領域 ←|→動摩擦力領域 ↑ | / | /F−f_d | /f_d ≡ mgμ_d |/ |/ |/ | f_d / +─────・────・────────────→ |/ f_0 外力F |/ |/ |/ |/ -f_d・ |
図B運動中の「外力-摩擦力 vs 外力」 </pre>
以下に式(4)の右辺の値に対応して説明する;
■■ 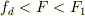 の場合■■
の場合■■
加速が減少したのと速度の初期条件が違うのを除き,(2)と同様に
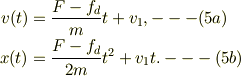
■■ 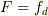 の場合■■
の場合■■
外力が動摩擦力とバランスしている場合である.運動は上の(5)と一緒だが,外力が加わっているのにも関わらず速度が一定であるのに注意.外力のする仕事は全て熱エネルギーに変換されている訳だ.スペース・シャトルが大気圏に突入してノーズが灼熱しているイメージに近いと思う.
■■ 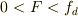 の場合■■
の場合■■
外力Fは正の値を保持しているが,運動方程式の右辺は負となる.従って,物体は減速を始める.
式(5)は成り立っているから,減速して停止する時間 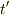 が決まる;
が決まる;
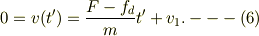
よって,
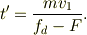
一度停止してしまうと,

なので再度の運動は起こりえない.
■■ 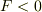 の場合■■
の場合■■
上の(6)と同じで,速度がゼロとなる.それ以降は方向が逆転するが(1)と同様の論議に戻る.
〜〜〜〜〜
以上で纏めを終了します.摩擦現象そのものも難しいプロセスに基づくらしいが,現象論的な「アモントン-クーロンのモデル」ですら,細かな場合分けを必要とすることを知りました.
大学の入試問題には「主たる問い」には出ないと思いますが,整理の参考になればと思います.
ミスが有れば,適宜修正します.