大学２年生 さんの書込 (2008/07/24(Thu) 14:18)

質問です．

問： 一様流が迎角を持つときの円柱周りの複素速度ポテンシャルとジューコフスキー変換を使って，平板周りの流線を描け． ただし，U,α,aの値は自分で決めてよい． （Uは定常流の速度（z⇒∞としたときのdw/dz），αは迎角，aは円柱の半径）

円柱周りの複素速度ポテンシャル W(ζ)=U・exp(-iα)・ζ + Ua^2・exp(iα)/ζ - i・Γ・ln(ζ/a)/2Π

という問題で， U=1,α=Π/4,a=2としてWに代入し， W(ζ)=exp(-i・Π/4)・ζ + 4・exp(i・Π/4)/ζ - i・Γ・ln(ζ/2)/2Π となったんですが，ここからどうやってジューコフスキー変換をすればいいのか わかりません． Z = ζ + 4/ζ をζについて解き代入して虚部をとってΨを決定しようとしたのですが，かなり複雑になってしまい断念しました． 極座標でやってみようともしましたが，うまくできませんでした． よろしくお願いしますｍ（＿＿）ｍ

toorisugari no Hiro さんのレス (2008/07/24(Thu) 23:18)

第1項と第2項に関しては 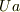でくくり，後はじっと見つめる．

大学２年 さんのレス (2008/07/25(Fri) 21:55)

W(ζ)=U・exp(-iα)・ζ + Ua^2・exp(iα)/ζ - i・Γ・ln(ζ/a)/2Π のはじめの２項をUaでくくってe^iαをcosα,sinαに分解して ジューコフスキー変換z/a = ζ/a + a/ζとして前の２項は処理できたのですが， i・Γ・ln(ζ/a)/2Πの部分が処理できません・・・． どうやったらいいんでしょうか？？ 返答お願いします．

なんとなく さんのレス (2008/07/26(Sat) 12:01)

横レス失礼します．

考え方は間違っていない気がしますが，問題の意図は”流線”ですから，ポテンシャルを経由せず，（複素）速度ベクトルでクッタ・ジューコフスキー変換すれば良いのではないでしょうか．それとα=π，Ｕ=1,a=2などの代入は意味がないと思います． 図を書くときに勝手に決めろ，ということでしょう．つまり決定すべきは循環Γのみです（ΓをU,α,aで表す）． しかし，流線の図が手で描けるのかしら？

大学２年生 さんのレス (2008/07/26(Sat) 13:55)

レスありがとうございます．

流線の定義がよくわかんなくなってきてしまいました． 流線って各点での速度ベクトルをつなげていったものですよね． 結局それはどのように書けばいいのでしょうか？？ dw/dzをジューコフスキー変換したものがそなまま流線になるのですか？？ 自分は流れ関数Ψを出してそれを描こうとしていたのですが・・・． Ψを微分したものが流線になるってことでしょうか？ 質問だらけですみません．

スチーム さんのレス (2008/07/26(Sat) 14:59)

>自分は流れ関数Ψを出してそれを描こうとしていたのですが・

そのように教科書に書いてありますが，概略を描くのであれば変換前の円の周りの流線からｖ＝０などの要点だけとりだして，類推して描くとどうでしょう． 正確な図は数値計算が必要では．

なんとなく さんのレス (2008/07/26(Sat) 16:23)

>大学2年生さん 混乱させてしまったなら，すみません．お書きのとおり，（複素速度ポテンシャ） w=（速度ポテンシャル）Φ＋i（流れ関数）ψとして，流線は流れ関数＝一定値の点を結んで行けばいいわけです． しかし，スチームさんが言われるように，数値計算が必要です．そこで，(複素速度ベクトル)v=dw/dz=ux-iuyの関係から，複素速度ベクトル場をジューコフスキー変換し，各座標点z=x+iyにおける速度ベクトル(ux,uy)を計算，格子点で図化（矢印等）すれば良いかな，と思ったわけです．その図はベクトル場の図化ですが，流線はそれを滑らかに結んだもので見えてくる筈と思ったのですが，それも簡単ではないようです．

toorisugari no Hiro さんのレス (2008/07/26(Sat) 18:37)

流線は流れ関数 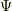の等高線になるわけで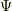， の関数形が得られれば，gnuplotなどで描画できます． あとは，ジューコフスキー変換やクッタの定理を使って，発生すべき循環を決定する事で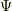， の関数形を決めればいいのでは?

スチーム さんのレス (2008/07/27(Sun) 13:18)

>i・Γ・ln(ζ/a)/2Πの部分が処理できません・・・． >どうやったらいいんでしょうか？？

流線関数は虚数部分なのでln(ζ/a)の実数部分ですね． ζ/aを極形式＝ｒe^(iφ） とおけば，ln(ζ/a)の実数部分はln(ｒ)です． ですから，ｚに変換したものの絶対値を算出すればよいと思います．

大学２年 さんのレス (2008/07/28(Mon) 21:30)

ln(ζ/a)の実数部分はζ/aを極形式＝ｒe^(iφ）とおけば，ln(ｒ/a)じゃないですか？？ そして，ｚに変換したものの絶対値を算出っていうのがよくわかんないです・・・． お手数ですが具体的に教えてくれませんか？？

スチーム さんのレス (2008/07/28(Mon) 22:51)

方針を書いてみます．参考にしてください． z/a = ζ/a + a/ζ を解くと ζ/a＝(ｚ＋√z^2-4a^2)/2a,(ｚ-√z^2-4a^2)/2a ここで ｚ＝x+yi を代入 ｚ＋√z^2-4a^2=x+yi+√(x^2-y^2-4a^2+2xyi) √(x^2-y^2-4a^2+2xyi)＝X＋Yiとおき， X,Yをもとめ，絶対値の自乗 (x+X)^2+(y+Y)^2 を計算

大学２年 さんのレス (2008/07/29(Tue) 20:22)

√(x^2-y^2-4a^2+2xyi)＝X＋Yiとおいて，２乗して (x^2-y^2-4a^2+2xyi)＝X^2 - Y^2 + i2XY 実部，虚部の恒等式から x^2-y^2-4a^2 = X^2 - Y^2 2xyi = i2XY

ここからX,Yが求まらないです・・・． 自分的にはいろいろ試行錯誤したつもりなんですが・・・．

スチーム さんのレス (2008/07/29(Tue) 21:14)

x^2-y^2-4a^2=Aとおく xy = XYより Y^2=x^2y^2/X^2 x^2-y^2-4a^2 = X^2 - Y^2 に代入 A=X^2 - x^2y^2/X^2 X^2をかけて X^4-AX^2-x^2y^2＝０ 解の公式 X^2={A＋√(A^2+4x^2y^2}/2 同様にして Y^2={-A＋√(A^2+4x^2y^2}/2

大学２年 さんのレス (2008/07/29(Tue) 21:51)

早い対応ありがとうございます． これからX,Yを出して(x+X)^2+(y+Y)^2に代入するってことですよね？？ かなり煩雑になりますね＞＜

スチーム さんのレス (2008/07/29(Tue) 22:26)

格子点ごとに座標の数値を代入してψを求め，等高線を描くことになるでしょう． 適当なソフト（マスマチカなど）をつかうと簡単．

大学２年 さんのレス (2008/07/31(Thu) 10:46)

なんとかできました＾＾ 皆さん本当にありがとうございました．

なんとなく さんのレス (2008/07/31(Thu) 13:02)

>大学２年生さん

できたということですので，答え合わせをされるなら，以下のURLに図が掲載されています．ただし，循環を逆向きに定義しているようなので，注意してください． 参考まで．

• http://slspc5.eng.shizuoka.ac.jp/homepage/lesson1/text4.pdf