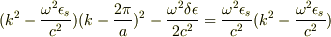変化する誘電体の分散関係

変化する誘電体の分散関係

メントス(4年) さんの書込 (2008/07/24(Thu) 13:11)

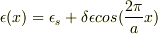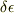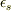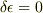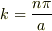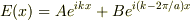大学院入試の問題です． 比誘電率が \epsilon(x)=\epsilon_{s}+\delta \epsilon cos(\frac{2\pi}{a}x) の物質中の電磁波の問題なのですが \delta \epsilon が \epsilon_{s} に比べて十分小さい場合を考える．分散関係は \delta \epsilon=0 のときとほとんど変わらないが， k=\frac{n\pi}{a} の近傍では散乱波の影響が無視できなくなり，分散関係は大きな変更を受ける．n=1の場合について考える． 波動方程式の解は E(x)=Ae^{ikx}+Be^{i(k-2\pi/a)x} と２つの平面波で近似できる．この式を波動方程式に代入し，左辺，右辺の 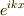e^{ikx} の係数および 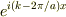e^{i(k-2\pi/a)x} の係数を比較することにより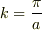， k=\frac{\pi}{a} 付近の分散関係を求めよ．

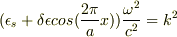
という問題で，実際に計算すると 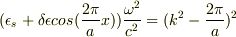(\epsilon_{s}+\delta \epsilon cos(\frac{2\pi}{a}x))\frac{\omega^{2}}{c^{2}}=k^{2} (\epsilon_{s}+\delta \epsilon cos(\frac{2\pi}{a}x))\frac{\omega^{2}}{c^{2}}=(k^{2}-\frac{2\pi}{a})^{2} と通常の分散関係において，誘電率を置き換えただけの式が出てきたのですが ここからどうすればいいのか分からず，いきづまってしまいました． よろしくおねがいします．

Re: 変化する誘電体の分散関係

mNeji さんのレス (2008/07/25(Fri) 00:02)

横からの逆質問をお許し下さい．

最近，「大学院入試の問題」という質問が多々有ります．別にそれ自身が駄目だという考えではありません．ただ，専門領域の質問だからといって「問題を省略して質問する」のには抵抗を感じます．

質問者さんと回答者さん以外にも多くの方がご覧になって，問題に対する考え方，判らないポイントなど，色々な角度から分析的にご覧になっていると思います．

その意味で，一字一句，原問題と同じ必要も無いでしょうが，原問題の物理的な背景は十分に復元できた形での質問をされるのが望ましいのではないでしょうか？

具体的に言えば； ＞比誘電率が 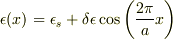\epsilon(x)=\epsilon_{s}+\delta \epsilon\cos\left(\frac{2\pi}{a}x\right) の物質中の電磁波の問題

此れだけでは，一次元の誘電体を考え，誘電率が余弦関数により周期的に変化する場合のでの，電場の振る舞いを論じろ...，とかですかね．

勿論，誘電体の問題としては標準的なのかも知れませんが，もう少し物理的な背景を示した質問を頂けたらと感じました．

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/26(Sat) 00:11)

＞という問題で，実際に計算すると （略） ＞と通常の分散関係において，誘電率を置き換えただけの式が出てきたのですが

略のところの数式に変数ｘが入っていておかしいです． ｘを含まないように複素指数関数の係数を比較する必要があるでしょう． あと，誘電率の変化項（cos(2π/a)x)を複素指数関数で置き換えてみるとどうですか．

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/07/28(Mon) 00:13)

＞mNejiさん 省略した部分ですが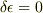， \delta \epsilon=0 としたときの導入的な問題で質問内容とあまり関係がなかったので，記事が長くなってしまうし，回答してくださる方も読むのが大変になるだろうと思い，書きませんでした． 問題の初期設定について省略した部分はないです．

＞スチームさん すみませんが，もう少しヒントをくれませんか？ 自分でもxを消去しようと試行錯誤してみたのですが，うまくいきません． 物質中の波動方程式に代入すると

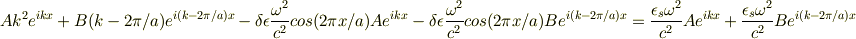
Ak^{2}e^{ikx}+B(k-2\pi/a)e^{i(k-2\pi/a)x}-\delta \epsilon \frac{\omega^{2}}{c^{2}}cos(2\pi x/a)Ae^{ikx}-\delta \epsilon \frac{\omega^{2}}{c^{2}}cos(2\pi x/a)Be^{i(k-2\pi/a)x}=\frac{\epsilon_{s} \omega^{2}}{c^{2}}Ae^{ikx}+\frac{\epsilon_{s} \omega^{2}}{c^{2}}Be^{i(k-2\pi/a)x}

となります．問題文の，「左辺右辺の係数を比較し，」という部分がよく分からないのですが，単純に 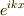e^{ikx} を両辺から消去すると

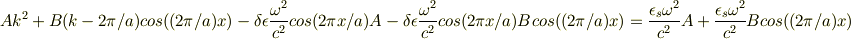
Ak^{2}+B(k-2\pi/a)cos((2\pi/a)x)-\delta \epsilon \frac{\omega^{2}}{c^{2}}cos(2\pi x/a)A-\delta \epsilon \frac{\omega^{2}}{c^{2}}cos(2\pi x/a)Bcos((2\pi/a)x)=\frac{\epsilon_{s} \omega^{2}}{c^{2}}A+\frac{\epsilon_{s} \omega^{2}}{c^{2}}Bcos((2\pi/a)x)

となりますが，xをどうやって消せば良いのか分かりません．

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/28(Mon) 08:47)

コサインと複素指数関数が混じっていると，やりにくいので， 2cosφ=e^(iφ)+e^(-iφ) を利用して，誘電率の項を表すと，全体が， e^(ikx),e^i(k-2π/a)ｘで表現できます， ただ，ほかに高振動数のものが出てきますが無視（近似）， これはあとでチェックする

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/07/29(Tue) 13:21)

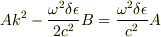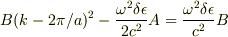2cosφ=e^(iφ)+e^(-iφ)として，係数を比べてみると Ak^{2}-\frac{\omega^{2}\delta \epsilon}{2c^{2}}B=\frac{\omega^{2}\delta \epsilon}{c^{2}}A と B(k-2\pi/a)^{2}-\frac{\omega^{2}\delta \epsilon}{2c^{2}}A=\frac{\omega^{2}\delta \epsilon}{c^{2}}B が出てきました． この2式からAとBを消去すればよいのでしょうか？

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/29(Tue) 13:42)

A,B消去すると分散関係がでてきます． あと，δが小さいことを用いて，ｋがπ/aの付近の近似式を作り， ωとｋのグラフを描くとよいと思います．

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/07/29(Tue) 14:21)

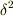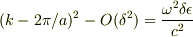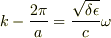式が複雑になって，うまく消去できないのですが \delta^{2} は無視しても良いのでしょうか？ 一番目の式のAを二番目の式に代入すると (k-2\pi/a)^{2}-O(\delta^{2})=\frac{\omega^{2}\delta \epsilon}{c^{2}} となりますが k-\frac{2\pi}{a}=\frac{\sqrt{\delta \epsilon}}{c}\omega ですか？ただの一次関数になってしまいました．

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/29(Tue) 14:47)

NO.21062の式に間違いがあると思います．δ＝０とするとｋ＝０になるので． δεとεsの混同があると思います．

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/07/29(Tue) 22:05)

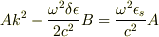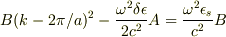すみません．右辺を書き間違えていました． Ak^{2}-\frac{\omega^{2}\delta \epsilon}{2c^{2}}B=\frac{\omega^{2} \epsilon_{s}}{c^{2}}A と B(k-2\pi/a)^{2}-\frac{\omega^{2}\delta \epsilon}{2c^{2}}A=\frac{\omega^{2} \epsilon_{s}}{c^{2}}B です．ここからどのようにしてAとBを消去すれば良いのでしょうか？

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/29(Tue) 22:21)

A=( )Bの形にして 第一式を第二式に代入してください．

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/07/29(Tue) 23:12)

(k^{2}-\frac{\omega^{2}\epsilon_{s}}{c^{2}})(k-\frac{2\pi}{a})^{2}-\frac{\omega^{2}\delta \epsilon}{2c^{2}}=\frac{\omega^{2}\epsilon_{s}}{c^{2}}(k^{2}-\frac{\omega^{2}\epsilon_{s}}{c^{2}})

となりました．複雑な形ですが，どこか近似するのでしょうか？

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/29(Tue) 23:57)

δεは２乗だと思います． このままでωとｋの関係が描けるはずですが，複雑です． k=π/a付近の分散関係を求めよ． という課題ですから， 新しい変数，仮にｘとして， k＝π/a+x を式に代入し，ｘの４次式を解の公式でｘの自乗をωで表し， δεが微小 ということを利用して近似式を作るとよいです．

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/07/30(Wed) 01:12)

ありがとうございます．ちょっと，やってみます． ところで，複素指数の計算について，ずっと引っかかっていたのですが，この問題の波は電磁波ですから 計算上は複素指数関数を使っていても，最後には実部を取るわけですよね？

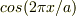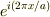ということは， cos(2\pi x/a) は e^{i(2\pi x/a)} と置き換えればよいのではないのですか？ いつも微分方程式を解くときなどはそうしているので，2cosφ=e^(iφ)+e^(-iφ)という置き換えが良く分かりません．(量子力学で，このように変形するのは分かります．) それと，もう一つ．

以前，この掲示板で教えていただいたのですが，複素指数関数同士をかけてしまうと，あとで実部を取ったときに答えが変わってしまいます．コサイン波を複素指数関数で表したとき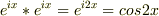， e^{ix}*e^{ix}=e^{i2x}=cos2x ですが，実際の波は 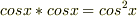cosx*cosx=cos^{2}x であるようにです． この問題の途中で，誘電体の複素指数と，電場の複素指数の積の計算をしてしまいましたが，それは大丈夫なのでしょうか？

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/07/30(Wed) 09:19)

>計算上は複素指数関数を使っていても，最後には実部を取るわけですよね？ >ということは，は と置き換えればよいのではないのですか？

波動方程式の解をFとする．他の解をGとする．線形だと， F+iGも解となる． これを利用しているわけです． つまり，実部も虚部も同じ方程式の解です． cosφをe^(iφ)に置き換えると方程式が異なってしまいます．

＞この問題の途中で，誘電体の複素指数と，電場の複素指数の積の計算をしてしま＞いましたが，それは大丈夫なのでしょうか？

これは解く過程は数学の問題ですから，物理的意味を心配することはないでしょう．

近似の方法ですが，もうすこし詳しく書くと，

k=π/a付近の分散関係を求めよ． という課題ですから， 新しい変数，仮にｘとして， k＝k0+x ω=ω0+y (k0=π/a,ω0=Ck0/εｓ） を式に代入し， ｘ，ｙ，δの高次の項を省略する近似を行う． つまり，ｘ＾２，ｙ＾２，ｘｙ，δ＾２を超える次数の項を省略． すると，双曲線が出てきます． 漸近線はδ＝０の場合で散乱が起きない場合を表しています．

この分散曲線の特徴はｋ＝ｋ０の付近でωが上下に分離し， 一定の範囲の振動数が存在できない領域ができることです． （禁止帯と呼ばれる．） フォトニック結晶とかで注目されているそうです．

Re: 変化する誘電体の分散関係

mNeji さんのレス (2008/07/30(Wed) 12:25)

＞フォトニック結晶とかで注目されているそうです．

なるほど，こんな分野もあったのですか...．

このスレッドの近くの「線密度が異なった弦の振動 えりさん， - 2008/07/26(Sat) 22:56 No.21010」は，一見すると大きな違いですが，部分的に波数が変動する領域が局在するという意味では，似た様な問題ですね．

一方が「誘電率の空間変化」，他方が「線密度の空間変化」という違いだけ，とは愉快な感じがします．

Re: 変化する誘電体の分散関係

メントス(4年) さんのレス (2008/08/07(Thu) 02:02)

返信が大変遅くなって，申し訳ありませんでした． 対称性になかなか気付かずに，計算に苦労していました．

＞(k0=π/a,ω0=Ck0/εｓ） ＞を式に代入し， ω0は次元から考えて 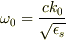\omega_{0}=\frac{ck_{0}}{\sqrt{\epsilon_{s}}} ではありませんか？

以前書いた，kとωの式が対称でない形だったので行列の永年方程式から

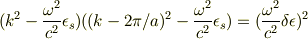
(k^{2}-\frac{\omega^{2}}{c^{2}}\epsilon_{s})((k-2\pi/a)^{2}-\frac{\omega^{2}}{c^{2}}\epsilon_{s})=(\frac{\omega^{2}}{c^{2}}\delta \epsilon)^{2}

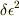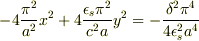
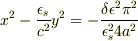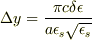と書いてみました． 教えていただいたxとyを代入すると，右辺のカッコのなかは一部の符号だけが違って，あとは同じものになります．右辺は \delta \epsilon^{2} の項だけが残って -4\frac{\pi^{2}}{a^{2}}x^{2}+4\frac{\epsilon_{s}\pi^{2}}{c^{2}a}y^{2}=-\frac{\delta^{2}\pi^{4}}{4\epsilon_{s}^{2}a^{4}} x^{2}-\frac{\epsilon_{s}}{c^{2}}y^{2}=-\frac{\delta \epsilon^{2}\pi^{2}}{\epsilon_{s}^24a^{2}} となって，いちおう双曲線になりました． グラフを書くと，π/a付近の振動数yは上下に分裂していて，そのギャップは \Delta y=\frac{\pi c\delta \epsilon}{a\epsilon_{s}\sqrt{\epsilon_{s}}} となりました． 合っていますでしょうか？

今までやったことのある近似は，マクローリン展開して二次まで残すとか 小さい項は無視する，のような大雑把なものばかりだったので，今回の近似の発想はかなり難しく感じました． kをxで置くところまでは理解できたのですが，同時にωも変換して，しかも二次の項は残すというのは，自分では全く思いつきませんでした・・・．

＞フォトニック結晶とかで注目されているそうです． この問題に，そのような背景があったのですね． 自分で最初に調べたとき，電磁気の本を見ていたのですが，まったく載っていませんでした． スチームさんのレスをみて，物性関係の本も調べてみたのですが，あまり詳しく載っているものは見つかりませんでした．かなり応用的な部分なのでしょうかね．

Re: 変化する誘電体の分散関係

スチーム さんのレス (2008/08/07(Thu) 08:56)

>ω0は次元から考えて ではありませんか？

そうです．訂正してください． メントスさんの結果で間違いはないと思います． 近似の方法は，たくさん経験つめば慣れてくるものです． フォトニック結晶は，散乱で検索していて見つけたもので， まだ，最近の研究過程のもののようです． みなさんのおかげで，勉強させてもらいました．