素人 さんの書込 (2008/07/24(Thu) 10:06)

大学1年生です．問題を解いていたのですが，答えがあるだけで途中の解き方，問題への取り組み方が分からず困っています．自分で解けるようになりたいのですが手掛かりを教えて頂けませんか？よろしくお願いします．

【問題】真空中をｚ軸の正の向きに進む角振動数ωの電磁波がある．電場はｘ軸方向に振幅Ｅ0で振動し， Ｅ（ｚ，ｔ）＝e1Ｅ0cos（ｋｚ−ωｔ）（e1はｘ軸正方向の単位ベクトル） で与えられるとして，次の問に答えよ．ただし，ω＝ｃｋ（ｃは光速）である．

（１）電磁波の磁場Ｂ（ｚ，ｔ）の大きさを求めよ． （２）Ｅ（ｚ，ｔ）の向きがｘ軸正方向のとき，Ｂ（ｚ，ｔ）の向きはどちらか． （３）電場および磁場のエネルギー密度Ｕe（ｚ，ｔ），Ｕm（ｚ，ｔ）をそれぞれ求め，それらが互いに等しいことを示せ． （４）この電磁波のポインティング・ベクトルＳ（ｚ，ｔ）の大きさを求めよ．

(１)については，調べてみたらマクスウェル方程式を当てはめて解けばいいみたいですが，使い方がよく分かりません． (２)〜(４)は，どう手をつけたら良いのか，分からずにいます． ほとんどをお聞きする形になってしまい，申し訳ありません． よろしくお願いします．

スチーム さんのレス (2008/07/24(Thu) 10:57)

とりあえずｙ方向の磁場Bをつぎのようにおいて，マクスウェル方程式に代入し，振幅B0を決定すればいいでしょう． ただし，e2はｙ方向単位ベクトル． B（ｚ，ｔ）＝e2B0cos（ｋｚ−ωｔ） （磁場と電場は直交しています．）

mNeji さんのレス (2008/07/24(Thu) 11:00)

素人さん，初めまして．

大昔の経験からすると，夏休みの段階まででマクスウェル方程式からエネルギ密度，その上ポインティング・ベクトルまでの問題を解こうとするのは気が早すぎるように感じます．

逆に，これらの事を理解していれば，ご質問の内容は自明に近いと思います．

＞(１)については，調べてみたらマクスウェル方程式を当てはめて解けばいいみたいですが，使い方がよく分かりません．

どの式を使えば良いと思い，そのどこが判らないのでしょうか？手始めにここから歩を進めるといいと思います．

素人 さんのレス (2008/07/25(Fri) 01:51)

スチームさん，mNejiさん早速のお返事ありがとうございます！！

今回代入するマクスウェル方程式について自分なりにも調べてみたのですが， スチームさんの言葉の「磁場と電場は直交している」ということから 公式の中の

∇・Ｂ＝０

または 「磁場と電場」を使用しているということから

∇×Ｅ＝−∂Ｂ/∂t

ではないかと考えているのですが，どうでしょうか？ 他にも，この代入する公式をどうやって活用すれば問題が解けるのか教えてもらえないでしょうか．

＞＞mNejiさん

mNejiさんに言われた通り，まだ気が早いのかとは思いますが，解き方が気になって仕方なかったので質問を書き込みました． わからないことだらけで申し訳ないですが，最後まで教えていただければ有難いです． どうぞよろしくお願いします．

mNeji さんのレス (2008/07/25(Fri) 06:45)

＞まだ気が早いのかとは思いますが，解き方が気になって仕方なかったので質問を書き込みました．

これは困って仕舞いますね．でも，その気持ちも判る様に思います．

大雑把に，どんな本をご覧になって，どの位，勉強されたのでしょうか？またベクタ解析の周辺の数学的準備は？

それらを無視してしまえば，この問題では，真空中を電場が平面波；

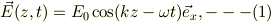
が進んでいる．この時の磁場を求めよと言う事になります．

この時に，単極磁荷がないことを意味する∇・Ｂ＝０を(1)に使う事は出来ませんが，真空中では電荷分布がないことから∇・Ｅ＝０に(1)を適応することは出来ます．ところが，この式では電場に関する情報が出て来るだけです．それは，進行方向と電場の方向とが直交するという情報です．

＃良い練習ですから，（１）について，その発散(Divergence)を取って，何が起こるか調べてみて下さい．

ですからマクスウェル方程式が判る為には，通常の電磁気の基本が判った上に，ベクタ解析の基本をマスタする必要があります．逆にいえば，これらを確り準備すれば，誰でもが必要に応じて，電気・磁気の現象を取り扱えるということです．

では，素人さんの現状をお聞かせ下されば，すこし説明方法を考えて見たいとおもいます．基本は，電磁誘導の式，∇×Ｅ＝−∂Ｂ/∂tの適用で良いと思います．

＃この式の左辺には（１）を代入して演算します．この右辺には，スチームさんのご紹介の磁場を代入して演算します．各項の常数項の比較から何が言えますか？

素人 さんのレス (2008/07/26(Sat) 22:59)

mNejiさん，回答ありがとうございます！！

この問題について，大学の先輩に手伝ってもらいつつなんとか答えにたどり着いてみました． 正直答えに自信がないのですが，これで合っているでしょうか？？

（１）Ｂ0＝Ｅ0/Ｃ，Ｂ（z，t）＝Ｂ0cos（kzーwt） Ｂ（z，t）＝Ｅ0/Ｃcos（kzーcost）

（２）Ｂ（z，t）ーＥ（z，t）＝０ Ｅ＝（z，t）＞０の時Ｂ＝（z，t）＞０より

ｙ軸方向

（３）Ｕe＝ε0Ｅ^2/２ Ｕｍ＝Ｂ^2/２Ｕ0なので Ｂ＝Ｅ/Ｃ，Ｃ＝１/√（ε0Ｕ0）より Ｕｍ＝（１/２Ｕ0）（Ｅ/Ｃ）^2＝（１/２Ｕ0）（ε0Ｖ0）Ｅ^2 ＝ε0Ｅ^2/２＝Ｕｅ

（４）ポインティングベクトルは， Ｓ（z，t）＝Ｅ（z，t）×Ｈ（z，t） ＝１/Ｕ0（Ｅ（z，t）×Ｂ（z，t）） ∴Ｂ＝（z，t）＝Ｅ0/Ｃcos（kzーcost），Ｃ＝１/√（ε0Ｕ0）より Ｓ＝（z，t）＝Ｅ0^2/Ｖ0Ｃcos^2（kzーεt） ＝√（ε0/Ｖ0）Ｅ0^2・cos^2（kzーεt）

となりました．よろしくお願いします！！

＞大雑把に，どんな本をご覧になって，どの位，勉強されたのでしょうか？

主に使っている本は「これならわかる理系の電磁気学」と「理系なら知っておきたい物理の基本ノート[電磁気学編]」です． 勉強した範囲についてですが，高校の時にきちんと基礎を積まなかったせいで，かいつまんでしか理解できていないような気がします．

＞またベクタ解析の周辺の数学的準備は？

div，rot，grad などの概念はなんとなくわかったと思うのですが，問題にうまく適用することができません．

mNeji さんのレス (2008/07/27(Sun) 00:08)

＞主に使っている本は「これならわかる理系の電磁気学」と「理系なら知っておきたい物理の基本ノート[電磁気学編]」です．

自分の全く知らない本ですが，本屋さんや近くの図書館で見てみます．私のお勧めは，砂川 重信・著，電磁気学の考え方，岩波書店，ISBN4-00-007892-5です．

＞勉強した範囲についてですが，高校の時にきちんと基礎を積まなかったせいで，かいつまんでしか理解できていないような気がします．

現時点で，電磁気の概観をすまされた訳ですから，夏休みに数学的な所を押さえながら，力学・電磁気学などを丁寧に考えれば宜しいかもしれません．私は古すぎるので，お若い方からのコメントをお願い出来れば良いですが...．

＞div，rot，grad などの概念はなんとなくわかったと思うのですが，問題にうまく適用することができません．

一般論で判るのと，実際の計算が出来るのとは，ちょっと別物ですよね．私は，若い頃，演習を馬鹿にしていて，痛い目に遭いました．要所に来たら，演習問題を一つくらいは解いておく方が，指の力が付くと思います(笑)．

力学や電磁気でのポテンシャルとgradの関係を確りと押さえ，電荷の保存側でdivをイメージするとかして，ベクタ解析と現象の関係をイメージできるようにすると良いですね．

問題は，rotですね．電磁誘導で出て来る電場の回転とかが，今回の電磁波の電場・磁場との関係するのですが，物理的な流れが複雑なのですぐにイメージ出来ないでしょうが，焦らないほうが良いと思います．

〜〜〜〜

＞正直答えに自信がないのですが，これで合っているでしょうか？？

と仰られても，すぐには判定できないので，（１）だけ計算してみましょう．

いま電場が既知なので，その回転を取ります．ただ電場がx方向だけで，z方向を向いた波であること;

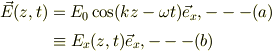
なので，計算が簡単になります．具体的に書き下すと；

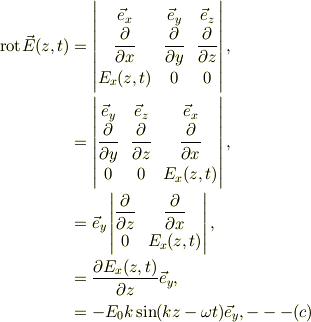
この右辺の正弦関数は余弦関数の時間微分で表せる，

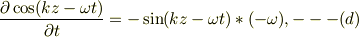
のに注意して，(c)を書き直すと

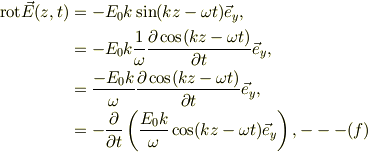
右辺の時間偏微分項は磁場に等しいのですから...．

素人 さんのレス (2008/07/27(Sun) 02:34)

とても丁寧に教えて下さって本当にありがとうございます！ 近々教えていただいた本を自分も調べてみて，力学と電磁気学の演習を混ぜつつ バランスよくやっていこうと思っています．

rotが出てくると，やっぱりイメージ的にも難しい感じがしますね．

mNejiさんが書いて下さった数式（f）を自分なりに整理しながら計算してみたのですが， 最終的な形として

Ｂ（z，t）＝e1・Ｅ0/Ｃ・cos（kzーωt）

となると考えていいのでしょうか？

あと，e1の部分についてですが，スチームさんが書いて下さっていた 「e2はｙ方向単位ベクトル」という風に考えて，e1の箇所をe2にして

Ｂ（z，t）＝e2・Ｅ0/Ｃ・cos（kzーωt）

と表した方がいいのでしょうか？ 度々質問してしまいすみません．

mNeji さんのレス (2008/07/27(Sun) 03:40)

＞最終的な形として ＞Ｂ（z，t）＝e1・Ｅ0/Ｃ・cos（kzーωt） ＞となると考えていいのでしょうか？

式(f)比較すべきは，ファラデイの電磁誘導の式；

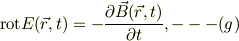
です．従って，時間についての偏微分の項が等しくなる事から，

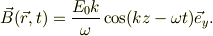
元々の電場は式(a)ですから此れと比較すると，波動成分；

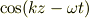
は共通ですが，方向と振幅とは違っています．

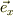方向は； ・電場で ， ・磁場で 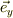， となり，直交しています．

振幅の係数は，波動性分の位相について，波の波長と周期が定まります．それらから波の位相速度に関係付けられます；

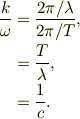
結局，磁場は；

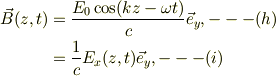
と表現できます．

スチームさんの最初のご助言，

＞ただし，e2はｙ方向単位ベクトル． ＞B（ｚ，ｔ）＝e2B0cos（ｋｚ−ωｔ）

とを比較すると，味わい深いですね．

スチーム さんのレス (2008/07/27(Sun) 09:43)

ひとつ気になるところは， 素人さんの解にベクトル，ベクトルの成分，スカラーの区別があいまいです． このところを正確にするようにと思いました．

mNeji さんのレス (2008/07/27(Sun) 10:18)

＞素人さんの解にベクトル，ベクトルの成分，スカラーの区別があいまいです． ＞このところを正確にするようにと思いました．

私も，少しそう思います．でも，ベクトルに慣れて来ると治ると思います．

今は物理的興味が強くて，前に前に転んでいる状態と思います．私は，このような勉強の仕方も多いに許されるべきと信じています．ですから，この夏休みに数学を充実されると，新学期からの物理に期待出来るのでしょうね．

素人 さんのレス (2008/07/31(Thu) 02:03)

返事が遅くなってしまってすいません！！

＞mNejiさん わかりやすい解説をありがとうございます． このように計算を進めていけばいいのですね． 答えや解説を見ると，解いていくことができるのですが，まだまだベクトル解析を使いこなすことができません． なので，これから時間をかけて徐々に覚えていこうと思っています．

＞スチームさん，mNejiさん 高校の頃からベクトルの問題が少し苦手なところがあり，自分の中でも誤魔化しながら進んできてしまった所があったので，その部分をこれから克服していきたいと思っています！ どうもありがとうございました！！

mNeji さんのレス (2008/07/31(Thu) 09:42)

＞このように計算を進めていけばいいのですね．

この手の問題の解法は，解き手によって様々だと思います．肝心なのは「進行する解」に「回転」を作用させたり，「時間偏微分」を作用させたりすると類似の成分になるという事だと思います．

＞答えや解説を見ると，解いていくことができるのですが，まだまだベクトル解析を使いこなすことができません． ＞なので，これから時間をかけて徐々に覚えていこうと思っています．

力学の場合は，質点の運動も，弦の振動も，量子力学的な粒子の運動も，運動方程式が一つですね．ところが，電磁気の波動となると，電場も磁場も一挙に関連して来て，ベクタの形式のマクスウェル方程式群を，扱う必要性が出て来ます．

その意味で，「物理的な現象の理解」と「数学的な処方箋の理解」は同時並行的に必要となります．素人さんは，曲がりなりにも前者を駆け足で学ばれた訳ですから，後者にも重要性を感じて欲しい所です．

なお，演習問題は数を沢山するよりは，問題毎に「物理的な特徴」とか「数学的な背景」などを自問自答しながら進む方が，結果的には効率的になるように思います．

素人 さんのレス (2008/08/08(Fri) 01:27)

わかりやすいご指導どうもありがとうございました！ これからも頑張ってみます！ また何かあったらご指導よろしくお願いします．