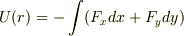えねるぎーと仕事
えねるぎーと仕事
ny さんの書込 (2008/07/21(Mon) 21:17)
質点にF=-k(x,y)という力が働くとき U(r)=-∫F(r)tds を利用して,(0,0)から(x,0).次に,(x,0)から(x,y)まで積分を行い,この力のポテンシャルを求めよ.
という問題です. 何をしたらいいのかさっぱりわかりません. どうして元の式がx成分とy成分と分かれているのに,答えでは一緒になっているのですか?問題にその本からの引用があったので少し文章を変えましたが,わかりますか? 出典は裳華房テキストシリーズ物理学です 答えは U(x,y)=k(x^2+y^2)/2 です.お願いします.
Re: えねるぎーと仕事
yama さんのレス (2008/07/21(Mon) 22:24)
U(r)=-∫F(r)tdsというのは 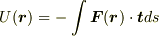 のことだろうと思います.
のことだろうと思います. 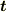 は積分経路の接線方向の単位ベクトルです.
これは,
は積分経路の接線方向の単位ベクトルです.
これは, 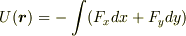 と表すこともできます.
と表すこともできます.
このような積分を用いてポテンシャルを求める問題は過去ログにもあります. たとえば,次の例が参考になるでしょう. ttp://hooktail.maxwell.jp/bbslog/20115.html
Re: えねるぎーと仕事
yama さんのレス (2008/07/22(Tue) 00:20)
積分経路の接線がx軸となす角度をφとすると, 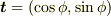 です.
従って
です.
従って 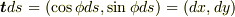 となるからです.
となるからです.
Re: えねるぎーと仕事
ny さんのレス (2008/07/22(Tue) 00:46)
わかりました.考え直してみます.
Re: えねるぎーと仕事
mNeji さんのレス (2008/07/22(Tue) 10:20)
横から失礼します.
ベクトル同士の内積はスカラ(普通の数)になるのをご存知ですよね.
簡単に2次元ベクトルの書き方を復習すると;
位置のベクトル
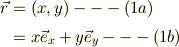
位置がずれた時の微小位置変化ベクトル;
![\Delta \vec r &= \Delta (x,y) &= (\Delta x, \Delta y) ---(2a)\\&=\Delta [x\vec e_x +y\vec e_y] &= \Delta x\vec e_x +\Delta y\vec e_y ----(2b)](http://hooktail.maxwell.jp/bbslog/8265a2f563e6e069e0602d9c3aac97d0.png)
ここで, 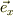 はx軸方向の単位ベクトルとします.
はx軸方向の単位ベクトルとします.
力のベクトルも
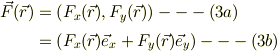
また,2つのベクトルの内積を次のように書きます;
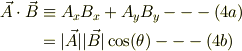
ここでベクトルの絶対値;
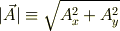
またベクトル 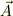 と
と 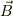 とが成す角度,
とが成す角度,  とします.
とします.
するとある物体が位置 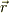 にいて,外力
にいて,外力 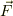 を受けて位置が
を受けて位置が 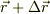 にずれたとする時に,外力が物体にする微量仕事は;
にずれたとする時に,外力が物体にする微量仕事は;
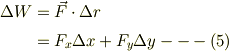
となります.他方,物体から眺めると,作用反作用の法則を考えると,物体は外部の系に 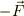 で仕事をするので,自分のもつエネルギは減少します,
で仕事をするので,自分のもつエネルギは減少します,
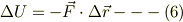
もしも,外力が位置の関数であったとすれば,
![\Delta U(\vec r) &= -\Delta W(\vec r) \\&= -\vec F(\vec r) \cdot \Delta \vec r\\&= -[F_x(x,y)\Delta x + F_y(x,y)\Delta y] ---(7)](http://hooktail.maxwell.jp/bbslog/8cdd4db666a8cfcbb8dcc8d568c20974.png)
となります.ある点 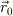 から経路Cを通って
から経路Cを通って 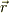 まで行く途中に細切れに(7)を出して,その総和を作ると,
まで行く途中に細切れに(7)を出して,その総和を作ると,
![U(\vec r) &= +U(\vec r_0 ) -\int_{C: \vec r_0}^{\vec r}\vec F(\vec r)\mathrm{d} \vec r\\&= +U(\vec r_0 ) -\int_{C: \vec r_0}^{\vec r}[F_x(\vec r)\mathrm{d} x +F_y(\vec r)\mathrm{d} y] ---(8)](http://hooktail.maxwell.jp/bbslog/7e9ed01928209ec6bf153c7ce65abcbe.png)
#とても簡略化した説明ですから,雰囲気だけ判るだけにとどめます.
大雑把な流れはこんな所です.記号が判らなかったりすれば説明します.
折角の夏休みを利用して,ベクトルの廻りの表現を勉強して下さいね.
Re: えねるぎーと仕事
ny さんのレス (2008/07/22(Tue) 21:03)
わざわざありがとうございます.私は大学1年生なのですが,担当の教授がぼそぼそっとしゃべる人で,よく授業が分かっておらず,仲間ともども困っているのです.明日そのテストがあります.