保存力と作用反作用の法則

DIO さんの書込 (2008/07/21(Mon) 11:43)

保存力の合力で与えられる力は必然的に作用反作用の法則を満たす，と思っているのですが，これは正しいでしょうか?? 以下に考え方を述べます．なお，これは『小出昭一郎著, 力学, 岩波書店』を参考にしました．

物体Aがn個の質点で，物体Bがm個の質点で構成されているとしてこれらの位置をそれぞれ 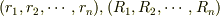$(r_1,r_2,\cdots,r_n),(R_1,R_2,\cdots,R_n)$ とします．物体Aの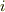番目の質点が，物体Bの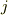番目の質点から受ける力がポテンシャルで表されるとすると，物体Aが物体Bから受ける力 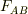$F_{AB}$ は

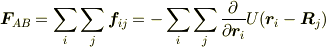
$\bm{F}_{AB} = \sum_{i} \sum_{j} \bm{f}_{ij} = -\sum_{i} \sum_{j} \frac{\partial}{\partial \bm{r}_{i}} U (\bm{r}_{i}-\bm{R}_{j})$

同様に，物体Bが物体Aから受ける力 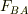$F_{BA}$ は

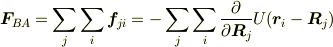
$\bm{F}_{BA} = \sum_{j} \sum_{i} \bm{f}_{ji} = -\sum_{j} \sum_{i} \frac{\partial}{\partial \bm{R}_{j}} U (\bm{r}_{i}-\bm{R}_{j})$

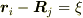となる．ここで $\bm{r}_{i}-\bm{R}_{j} = \xi$ とおくと，

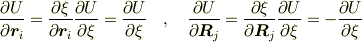
$\frac{\partial U}{\partial \bm{r}_{i}} = \frac{\partial \xi}{\partial \bm{r}_{i}} \frac{\partial U}{\partial \xi} = \frac{\partial U}{\partial \xi} \quad , \quad\frac{\partial U}{\partial \bm{R}_{j}} = \frac{\partial \xi}{\partial \bm{R}_{j}} \frac{\partial U}{\partial \xi} = -\frac{\partial U}{\partial \xi}$

となるので，これより

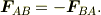
$\bm{F}_{AB} = -\bm{F}_{BA}.$

また，分子間力は保存力なのでしょうか?? もしそうであれば，抗力や張力といった力は分子間力の合力ですので，これらは上の考え方に当てはまるのですが，

よろしくお願いします．

Re: 保存力と作用反作用の法則

yama さんのレス (2008/07/21(Mon) 12:57)

作用反作用の法則は，空間の一様性から導かれるものであって，保存力だから成り立つというものではありません．一般に，保存力のポテンシャルは２つの質点の位置の関数 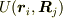$U(\bm r_i,\bm R_j)$ ですが，それだけでは

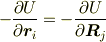
$-\frac{\partial U}{\partial{\bm r_i}}= -\frac{\partial U}{\partial{\bm R_j}}$

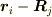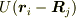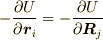が成り立つとは言えません．しかし，空間の一様性を仮定すれば，ポテンシャルは２質点の相対的な位置関係だけで決まることになるので， $\bm r_i-\bm R_j$ の関数 $U(\bm r_i-\bm R_j)$ になり，従って $-\frac{\partial U}{\partial{\bm r_i}}= -\frac{\partial U}{\partial{\bm R_j}}$ が成り立つことになります．

Re: 保存力と作用反作用の法則

スチームさんのレス (2008/07/21(Mon) 13:13)

話が本筋と違うかもしれませんが，作用反作用の法則が成り立たない力の例としては，どのようなものがあるでしょうか．

Re: 保存力と作用反作用の法則

DIO さんのレス (2008/07/21(Mon) 14:07)

返信有り難うございます．

>yamaさんすみません，空間の一様性とはどういった事でしょうか?? 空間の一様性を保証するのが作用反作用の法則の本質ということでしょうか??

>スチームさん恐らくそのような例は無いと思います．

Re: 保存力と作用反作用の法則

yama さんのレス (2008/07/21(Mon) 20:54)

空間の一様性とは，系全体を平行移動させても系の力学的性質（を表すラグランジアンやハミルトニアン）が変化しないということです．あるいは，座標系を平行移動させても同じことです．座標系の平行移動によってポテンシャル 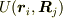$U(\bm r_i,\bm R_j)$ が変化しないためには，ポテンシャルが 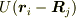$U(\bm r_i-\bm R_j)$ の形でないといけないわけです．

作用反作用の法則についてはいろいろな側面からの議論がありますが，空間の一様性の現れであるとは言えるでしょう．

Re: 保存力と作用反作用の法則

DIO さんのレス (2008/07/21(Mon) 22:21)

有り難うございます．よく分かりました．

少し話が逸れるのですが，非保存力とは部分部分で見れば保存力なのでしょうか?? そうでなければポテンシャルで表せないため，上のようにはできません．もしくは非保存力の時の作用反作用は別の方法で説明できるのでしょうか．

Re: 保存力と作用反作用の法則

yama さんのレス (2008/07/21(Mon) 22:55)

部分部分で見るというのが，たとえば摩擦力を原子や分子の間にはたらく力に分解して考えるということなら，それらの力は確かに保存力ですね．摩擦力を巨視的な力のまま扱うとすれば，それをラグランジアンの中に取り入れることはできないので，平行移動に対するラグランジアンの不変性を用いることはできないでしょうね．

Re: 保存力と作用反作用の法則

DIO さんのレス (2008/07/22(Tue) 22:36)

有り難うございます．とても理解が深まりました．

Re: 保存力と作用反作用の法則

DIO さんのレス (2008/07/23(Wed) 19:57)

もう一度質問させてください．

ポテンシャルで表せない力，ローレンツ力の磁気成分などの作用反作用についてなのですが，これについては先のような考え方と関連は無いのでしょうか??

凄くアバウトな質問で申し訳ないのですが，，

Re: 保存力と作用反作用の法則

yama さんのレス (2008/07/25(Fri) 00:13)

ローレンツ力がはたらくのは，たとえば２個の荷電粒子が互いに運動している場合ですね．荷電粒子Aが荷電粒子Bに及ぼす力を求めるには，AがBの位置につくる電磁場をリエナール-ヴィーヒェルトのポテンシャルを利用して求め，その電磁場からBが受けるローレンツ力を計算すればいいわけです．ところが，リエナール-ヴィーヒェルトのポテンシャルを計算するときにはAの位置や速度を用いますが．その位置や速度は過去の時刻における位置や速度です．それに対してローレンツ力を計算するときのBの速度は現在の速度です．これは作用が有限の速さで伝わるためですが，このように異なる時刻の位置や速度をラグランジアンの中に取り入れることはできません．ラグランジアンに含まれる座標や速度は同一時刻のものでないといけないからです，従ってラグランジアンを利用して作用反作用の法則を導くことはできません．作用が瞬間的に伝わるわけではないので，ある瞬間の作用と反作用が一般には等しくならないのは当然でしょう．

作用反作用の法則を成り立たせるには電磁場をラグランジアンの中に含める必要があります．電磁場自体がエネルギーや運動量を持ち，荷電粒子との間でエネルギーや運動量を交換すると考えるわけです．そうすると荷電粒子と場との相互作用や近接する異なる点の場の相互作用について作用反作用の法則が成り立つと考えることができます．

Re: 保存力と作用反作用の法則

DIO さんのレス (2008/07/25(Fri) 00:58)

回答有り難うございます．

なるほど，ローレンツ力が簡単に作用反作用が成り立ってくれないのは荷電子が運動しているときを考えなければいけないからなんですね．

と言うことは，重力でも二つの質点が互いに運動していれば電磁気力と同様に場自信の運動量，エネルギーを考慮しなければならなくなるのでしょうか

Re: 保存力と作用反作用の法則

yama さんのレス (2008/07/26(Sat) 00:06)

非相対論的な場合は，万有引力が瞬間的に伝わるので，場のエネルギーや運動量を考える必要はありません．しかし，一般相対論で考える場合は，重力場のエネルギーや運動量も考慮する必要があります．とはいっても，たとえば水星の近日点の移動を計算する程度なら，重力場自身のエネルギーをを無視する近似で十分です．なお，重力場のエネルギーの定義についてはいろいろな議論があるようです．

Re: 保存力と作用反作用の法則

DIO さんのレス (2008/07/26(Sat) 09:10)

有り難うございました．一般相対論については未習なので，重力場の概念は少し早すぎたようです．

作用反作用に関しては，力の伝わる速度が有限かつ２体が互いに運動しているときを除けば，空間の一様性を認めれば，先（No.20928）のように成り立つ．という事ですよね，

有り難うございました．

[home] [掲示板] [ページの先頭]