平均場近似？

メントス(4年) さんの書込 (2008/07/20(Sun) 12:11)

大学院試験の過去問題です．今回は分からなかった部分があるわけではないのですが，自信がないので，添削をお願いできますか？

N個のイジングスピンからなる系を考える．スピンiとスピンjの間の相互作用を 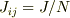$J_{ij}=J/N$ としたとき，ハミルトニアンは 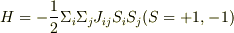$H=-\frac{1}{2}\Sigma_{i} \Sigma_{j}J_{ij}S_{i}S_{j} (S=+1,-1)$ である．磁化を 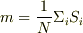$m=\frac{1}{N}\Sigma_{i}S_{i}$ と定義する． 1，mが与えられたとして，1スピンあたりのエネルギーを求めよ． 2，1スピンあたりのエントロピーを求めよ． 3，自由エネルギーを最小にするmの方程式を求めよ．というものです．

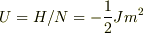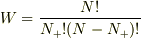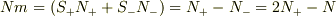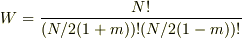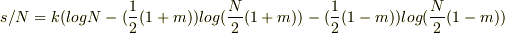
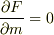最初，問題文が把握できなくて面食らっていたのですが定義された磁化mというのは，N個のスピンを平均したもの(係数を考えずに無次元化した平均磁化)，という解釈で合っていますか？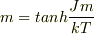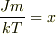それで進めていくと $U=H/N=-\frac{1}{2}Jm^{2}$ 状態数は $W=\frac{N!}{N_{+}!(N-N_{+})!}$ また，全スピンの和は $Nm=(S_{+}N_{+}+S_{-}N_{-})=N_{+}-N_{-}=2N_{+}-N$ だから mを使って状態数を表すと， $W=\frac{N!}{(N/2(1+m))!(N/2(1-m))!}$ となってエントロピーはスターリングの公式を使い $s/N=k(logN-(\frac{1}{2}(1+m))log(\frac{N}{2}(1+m))-(\frac{1}{2}(1-m))log(\frac{N}{2}(1-m))$ $\frac{\partial F}{\partial m}=0$ より $m=tanh\frac{Jm}{kT}$ となりました． $\frac{Jm}{kT}=x$ として，グラフを書くと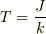， $T=\frac{J}{k}$ で相転移すると思います．

これは平均場近似の問題だと思うのですが，問題集などで類題をみると近接点の数zというのが与えられています．この問題には与えられていませんが，何次元の問題なのでしょうか？数式を計算していくうちに問題は解けましたが，いまいちイメージできないです．

追記ウィキペディアで調べたところ，磁性相転移温度は 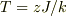T=zJ/k となるようなので，今の場合はz=1? 隣接点の数が1というのはおかしいですね・・・．

Re: 平均場近似？

nomercy さんのレス (2008/07/20(Sun) 18:46)

>ウィキペディアで調べたところ，磁性相転移温度はとなるようなので，今の場合はz=1?

結合定数に1/2を付けたり，付けなかったりするのでまずはそこを確認してみて下さい．

Re: 平均場近似？

メントス(4年) さんのレス (2008/07/20(Sun) 20:42)

ご指摘のとおり，ウィキぺディアの場合は結合定数をJで定義していました．今はJ→J/2ですから，z=2ということになりますね．つまり，一次元の問題ということでしょうか？

Re: 平均場近似？

スチームさんのレス (2008/07/20(Sun) 21:14)

１次元イジングモデルでは相転移しないといわれています．どこかに間違いがないでしょうか．

Re: 平均場近似？

nomercy さんのレス (2008/07/20(Sun) 21:39)

>つまり，一次元の問題ということでしょうか？

その通りです．

>１次元イジングモデルでは相転移しないといわれています．

厳密にはそうですが，平均場近似では相転移が生じます．

Re: 平均場近似？

メントス(4年) さんのレス (2008/07/21(Mon) 00:37)

ありがとうございます．スピンが一直線に並んでいて，隣同士だけ相互作用しあうという感じですね．計算の途中過程に変なところはないでしょうか？たぶん，答えに行き着いたので大丈夫だと思いますが．

ところで，私は「統計力学の解法＝分配関数」と思っていたのですが，この自由エネルギーを最小にする，というのもメジャーな方法なのでしょうか？この問題を分配関数で解いてみました．

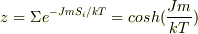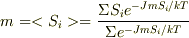
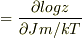
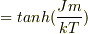
一スピンあたりの分配関数は $z=\Sigma e^{-JmS_{i}/kT}=cosh(\frac{Jm}{kT})$ となり平均磁化mは $m=<S_{i}>=\frac{\Sigma S_{i}e^{-JmS_{i}/kT}}{\Sigma e^{-JmS_{i}/kT}}$ $=\frac{\partial logz}{\partial Jm/kT}$ $=tanh(\frac{Jm}{kT})$