T.U さんの書込 (2008/07/19(Sat) 19:31)

院試の過去問で質問があり,分かる方が教えて頂ければ助かります．

問題は「無限に長い２本の平行直線ＡとＢが距離２aを隔てて置いてあり，それぞれ正と負の電荷が線密度λと-λで一様に分布している．直線ＡとＢからそれぞれ距離RaとRbだけ離れた点Ｐでの電位を求めよ」です．

まず，この問題で直線は半径aの導線であると仮定して良いものでしょうか？ もし出来ない場合，どうやって積分範囲を決めるか教えていただけないでしょうか？

以下は直線が半径aの導線であると仮定した場合の私の答えですが， これであっているのでしょうか？

1. 無限に長い直線上の電荷による電場はE=λ/(2πE0r)

2) 二つの直線による電場は下記の通りとなり （注： 直線Ａに垂直にＢの方向にｘ軸を取り，d = Ａ，Ｂ間の距離）

E=λ/(2πE0x) - -λ/(2πE0[d-x])

3) aからRaに積分して 電位= -λ/2πE0 (a->Raの積分）(1/x + 1/d-x) dx 電位 = - (λ/２πE0log (Ra/Rb)((d-a)/a))

4. A->Bの距離dは2a+a+a=4a で正しいのでしょうか？

以上よろしくお願いします．

mNeji さんのレス (2008/07/19(Sat) 20:22)

電場を，両方の電線に垂直な平面で考えます．それぞれの電線が単独で存在する時は電場は導線を中心にした同心線上で一定ですが，両方の電線が同時に存在すると，たとえ両電線の中間点を考えても，同心分布にはなりませんね．

他方，各電線のポテンシャルはスカラですから個別に加えても良い筈ではないでしょうか．

yama さんのレス (2008/07/19(Sat) 20:33)

問題の意味が正しくつかめていないのではないかと思います．

まず，直線ということは太さが無視できるということです． また，Pを含み，直線に垂直な面内で△APBを考えたとき AB=2a，AP=Ra，BP=Rb であるということです．

ポテンシャルを求めるには，片方の直線電荷だけによるポテンシャルをそれぞれ求めて，それらの和をとればいいでしょう． 電場の積分によってポテンシャルを求める場合の積分経路はPから無限遠になります．（ただし，無限遠でのポテンシャルを0とする場合です．）

T.U さんのレス (2008/07/20(Sun) 00:08)

mNejiさん，yamaさん，質問に答えて頂きありがとうございました．

電場の積分でポテンシャルを求める場合は，下記のようで正しいでしょうか？

無限に長い直線上の電荷による電場は，E(r) = λ / (2πε0r) で， a=無限として

Aによる電位

Ra φ(r) = - ∫ λ/(2πε0r)dr = λ/(2πε0) log a/Ra a

Ｂによる電位

Ra φ(r) = - ∫ -λ/(2πε0r)dr = λ/(2πε0) log Rb/a a

電位Ａ＋Ｂ= λ/(2πε0)log Rb/Ra

yama さんのレス (2008/07/20(Sun) 01:30)

合っていると思います．

この場合はポテンシャルの基準点をABの中点にとって計算したことになりますね． 無限遠でのポテンシャルを0とするのは片方の直線電荷だけによるポテンシャルを求める場合には適切でなかったようです． 片方だけ考えた場合はポテンシャルが無限遠で発散するからです． しかし，両方の直線電荷によるポテンシャルは無限遠で0になりますね．

ポテンシャルがRaとRbの比だけに関係するというのはおもしろいですね． そうすると等ポテンシャル面の形状はどうなるでしょうか？考えてみてください．

mNeji さんのレス (2008/07/20(Sun) 09:59)

＞電位Ａ＋Ｂ= λ/(2πε0)log Rb/Ra

なにか条件が不明確なままに回答が出てしまうのには，納得しにくいですね．

所謂，正の電荷と負の電荷が近接して分布する場合の「双極子」の一つとおもいますが，ご呈示の計算では，正負の電荷間距離が明示的に入っていません．

やはり座標系を定義して，それぞれの電線中心から一定点までの距離をパラメータにしてポテンシャルを出しておく方が，イメージがハッキリすると思います．

勘違いでしたら，ご免なさい．

T.U さんのレス (2008/07/21(Mon) 00:17)

yama, mNejiさんありがとうございました．

さて，mNejiさんのご指摘の点ですが，もしよろしければこの場合の座標系の定義の仕方を詳しく教えていただけないでしょうか？

mNeji さんのレス (2008/07/21(Mon) 00:49)

＞もしよろしければこの場合の座標系の定義の仕方を詳しく教えていただけないでしょうか？

大学院の試験問題を第三者が解くというのは余りにも奇妙な状況と思います．

やはり，問題を明確にご呈示の上，ご自分のお考えをお示しにならないと意見を申し上げられないと思います．

yama さんのレス (2008/07/21(Mon) 01:21)

Aの電荷によるポテンシャルはAからの距離Raだけで決まります． Bの電荷によるポテンシャルはBからの距離Rbだけで決まります． AとBの電荷によるポテンシャルは，これらの和になるのでRaとRbだけで決まります． 従ってRaとRbを用いてポテンシャルを表す場合には，AB間の距離は現れません．

もちろんデカルト座標でポテンシャルを表す場合は，AB間の距離（2a）が現れます． また，ポテンシャルの勾配をとって，電場を求める場合もAB間の距離が現れます．

mNeji さんのレス (2008/07/21(Mon) 10:12)

yamaさん，

逆に言えば，問題の文脈が判らないと何が正しい解答か判らないのだ，とおもいます．推定では，複数の設問から成り立っているかと思っています．従って，私の意見は「？」を強調しましたが，間違いと断定していません．

ただし，ポテンシャルの定数項が落ちたのは，それぞれの電線の半径をdと仮定した事によりますが，それは原点の決定から導かれた結果でないと感じたので，座標系の取り方について気にした，という事です．

＃そもそも「電線の半径をdと仮定」がどうして出て来るのか，不思議です．

私見ですが，電磁気学だけでなく，力学も，およそ物理の問題に接する時には，高校生の段階から「問題を解くには，正しい座標系の設定」に注意を払うべきだと感じます．

yama さんのレス (2008/07/21(Mon) 13:26)

TUさんは，最初は導線の半径をa，AB間の距離をdとして解かれていましたが，それについて問題の意味が正しくつかめていないのではないかと指摘したわけです．

問題文からは，直線Aと直線Bの距離は明らかに2aであると読みとれます． また直線なのでその太さは無視できることになります．つまり半径は無限小です． 「直線ＡとＢからそれぞれ距離RaとRbだけ離れた点Ｐでの電位を求めよ」ということは，RaとRbを用いてPの電位を表せということだと思われます．

TUさんの２回目の計算では，問題の意味に沿って計算できていると思います．

なお，この結果を用いれば，ポテンシャルをデカルト座標で表すのは簡単です． ABの中点を原点にとり，Aの座標を(a,0)，Bの座標を(-a,0)として

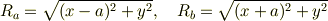
と置けばよいからです．

T.U さんのレス (2008/07/22(Tue) 00:18)

mNejiさん，yamaさん，ありがとうございました．

教えて頂いたポイントをもう一度考え，自分なりに納得がいくまで考えてみようと思います．