PHAs さんの書込 (2008/07/19(Sat) 11:13)

ｌＢｌ ｌ■ｌＡ→左図のように水平で滑らかな床の上に，しつりょうＭ ｌ＿＿＿＿＿＿ｌ幅Ｌのはこがあり，箱の中に質量ｍの小さい物体が ＿＿＿＿＿＿＿＿＿＿おかれている． このはこに長さの方向に水平で一定のおおきさのちからＦを加えて，はこをうごかした．次の各問いに答えよ．（重力加速度＝ｇ，物体とはこの底面の間の静止摩擦係数＝μ．） （１）物体が箱に対して静止しているための，力Ｆcの最大値を求めよ． これはFc=μ．ｍｇであってると思っています．

それで，わからないのが次の問題なのですが，

（２）前門のＦｃよりも大きい力Ｆを箱に加えたとき，力を加え始めてから物体が左端Ｂに達するまでの時間ｔ．を求めよ．ただし，物体とはこの底面との間の動摩擦係数をμとする（μ＜μ．）．

という問題なんですが，この問題をＭとｍごとに運動方程式を立てて，（Ｍの加速度をα，ｍの加速度をβ）（−β）ーαでＭに対するｍの相対加速度をだして，

Ｌ＝０・ｔ+1/2{（−β）ーα}・（ｔ２乗）に代入してｔについてといてみたのですが，問題文中の（μ＜μ．）を計算途中で使ってないのでどうも引っかかっています．ここはなにか↑意味があるのでしょうか？

ちなみに答えは・・・書きにくいのですが．．． ｔ＝√２ＬＭ/μｇ（Ｍ+２ｍ）−２Ｆ となったのですが．．あっているのでしょうか？

草々

DIO さんのレス (2008/07/19(Sat) 13:35)

(1)を間違えられています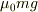． というのは静止摩擦力の最大値です．

(2)は考え方は良いように思いますが，答えは間違っていると思います．相対加速度を 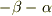とされているのが気になります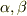， を両方 の方向を正ととっているなら相対加速度は になるはずです．

なお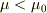， は計算過程で出てくることは無いかと思います．これが成立していないとおかしい，というだけです．(1)を考え直して(2)の答えをきちんと出せれば，その意味が分かるかと思います．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/07/22(Tue) 10:12)

ＤＩＯさんがレスを書かれたあと進んでいないようですね．

ＤＩＯさんは ＞(1)を考え直して(2)の答えをきちんと出せれば，その意味が分かるかと思います． と書いておられますが手が付かないままなのではないでしょうか．

ＰＨＡｓさんは ＞この問題をＭとｍごとに運動方程式を立てて，（Ｍの加速度をα，ｍの加速度をβ）（−β）ーαでＭに対するｍの相対加速度をだして，・・・

と書いておられますが運動方程式はきちんと出来ていますか． 相対加速度など考えようとせずにＡ，Ｂそれぞれについてきちんと運動方程式を立てて考えてみるといいと思います．式が出来れば普通に解けばいいです．相対加速度はその中で自然に出てきます． 運動方程式を立てることができるというのはＡ，Ｂそれぞれがどういう運動をするのかがきちんと分かっているということです．運動のイメージがつかめていないと運動方程式を立てることは出来ません．計算を簡略にする方法として相対運動を考えるというのはその後のことです．箱と物体の床に対する運動を運動方程式で表すという立場であれば慣性力は関係ありません．理解不十分なまま慣れていない方法を使う必要はありません．（質問のタイトルが「慣性力」となっています．こういう問題は慣性力で考えなければいけないと思っておられるように感じました．）

（１）が間違っていると指摘されていますがどうしてだめなのかが分からないのではないでしょうか．運動のイメージが出来ていないことになります．

箱には外力Ｆが働いていますが物体には摩擦力ｆ以外の力は働いていません．この２つの力で箱と物体のそれぞれが運動します．（箱には摩擦力の反作用も働きます．）

(１)では物体は箱と一体になって運動します．箱に対して静止しているというのは床に対して静止しているというのとは違います． （２）では別々の加速度で運動しています．

違いはこれだけです． （１）ではα＝βです．摩擦力は静止摩擦力です． （２）ではα≠βです．摩擦力は運動摩擦力です． この違い以外は同じ式です． 式を立てて解いてみてください．

（１）ではｆ≦μ．ｍｇという条件からＦの条件が決まります．常にＦ＞ｆが成り立つはずですからＦ＝μ．ｍｇということはありません．

PHAｓ さんのレス (2008/07/23(Wed) 13:41)

返答ありがとうございます，そして返信野間が開いてしまったこと申し訳ありません．家のパソコンに親がパスかけててログインできず・・学校からやるしかないもので．．． たしかに（１）では運動方程式考えずにやっていたのでまちがえてあたりまえでしたね・・（トホホ）

（２）は運動方程式はｍa=μｍｇ−ma（←が少し不安ですが） Mβ＝F−μｍｇ をといてやったら（Texが使いたいが学校からなので時間がない．．） ｔ＝√２ｌｍ/(M+2m)μｇ−２Fになりました． （ーｂ）−aだとたしかに√２ｌ/μｇとかいう不自然な形になりました

本当に助かりました．ありがとうございます．

（２週間前に物理はじめたばかりなので・・・・・・一応こう３ですが・・ 類型学習時間７・５時間）

草々（いや，本当に時間がないんです）

ｋｏｍａｇａｔａｋｅ さんのレス (2008/07/23(Wed) 19:44)

＞（２）は運動方程式はｍa=μｍｇ−ma（←が少し不安ですが）

この式はおかしいです．

２つの物体が繋がっている場合の運動の例は教科書の必ず載っていると思います． 紐で繋がっている場合， 後ろの物体が前の物体を押している場合， 小さい物体が大きい物体の上に乗っている場合， ・・・ どれも考え方は同じです． たいていは２つの物体が同じ加速度で動いている場合です． 滑車の両側に質量の異なる物体がぶら下がっている場合というのもあります．

ここでの問題は２つの物体が異なる加速度で運動するのですから少しだけ違います．でも違うのは加速度だけです．

基本的な考え方をきちんと押さえておかないとちょっと表現が変わッただけで立ち往生ということになってしまいます．