質問です

ベルク[大学１年] さんの書込 (2008/07/16(Wed) 17:09)

【問題】力が下の式で与えられるとする．Ｆx=a[11]x＋a[12]y＋a[13]z Ｆy=a[21]x＋a[22]y＋a[23]z Ｆz=a[31]x＋a[32]y＋a[33]z

(1)保存力である条件を求めよ． (2)その場合のポテンシャルを求めよ．原点を基準にとる．

という問題が大学の期末で出題されました．正答率が低いらしいのですが，解答がありません．教えてください．よろしくお願いします．

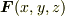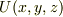保存力 $\bm{F}(x,y,z)$ とポテンシャル U(x,y,z) の間にどのような関係がありますか?

関数 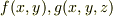f(x,y), g(x,y,z) が「2回偏微分可能」である条件は?

仮にポテンシャルが

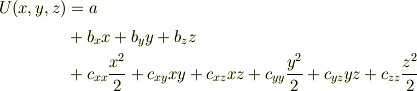
$U(x,y,z) &= a \\&+ b_x x +b_y y +b_z z \\&+ c_{xx} \frac{x^2}{2} + c_{xy} xy + c_{xz} xz + c_{yy} \frac{y^2}{2} + c_{yz} yz + c_{zz} \frac{z^2}{2}$

の形( 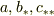$a,b_{*},c_{**}$ は定数)のとき，力はどう表されますか?

(追記)式を修正しました．

返信ありがとうございます． (1)ですが，自分は(回転)=0から a[12]=a[21] a[23]=a[32] a[31]=a[13]を得ました．

(2)は，公式(?)に沿って計算して６項の交代式になったのですが…

ポテンシャルがその形のとき，力がどう表されるかは分かりません．すみません．

> (1)ですが，自分は(回転)=0から > (2)は，公式(?)に沿って計算して６項の交代式になったのですが…

2次元では1個の，3次元では3個の式になります．ポテンシャルが「2回偏微分可能」と保存力の「(回転)=0」はおなじ事です．

> ポテンシャルがその形のとき，力がどう表されるかは分かりません．

ポテンシャルと保存力の間の関係式を考えれば一発です．

ありがとうございます．ポテンシャルの式を偏微分して力の式が得られれば，合っていると判断してイイでしょうか

> 合っていると判断してイイでしょうか

なにが「合っている」のか示してくれないとわかりません．