波動関数と角運動量の大きさ
波動関数と角運動量の大きさ
メントス さんの書込 (2008/07/15(Tue) 15:59)
わからない問題が出てきたので,お願いします.
波動関数が 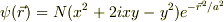 で与えられるとき,粒子の軌道角運動量の大きさを求めよ.(N,aは定数で,iは虚数単位です.)
で与えられるとき,粒子の軌道角運動量の大きさを求めよ.(N,aは定数で,iは虚数単位です.)
量子力学で物理量を求めるときは,
1,固有関数で展開
2,演算子を作用させる
のどちらかだと思うのですが,軌道角運動量の固有関数 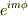 の形になりそうもないので,
の形になりそうもないので, 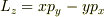 をかけて,素直に微分してみました.
答えは,
をかけて,素直に微分してみました.
答えは, 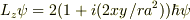 となり,一応
固有値方程式の形にはなったのですが,
となり,一応
固有値方程式の形にはなったのですが, 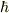 の整数倍になりませんでした.
そもそも,
の整数倍になりませんでした.
そもそも, 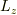 の固有値が求められたところで,
の固有値が求められたところで, 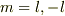 のときを求めないと意味がないので,行き詰ってしまいました.
もっと別の方法があるのでしょうか?
のときを求めないと意味がないので,行き詰ってしまいました.
もっと別の方法があるのでしょうか?
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/15(Tue) 17:44)
ぱっと見た所,波動関数も演算子も極座標表示にしたらどうでしょうか.
Re: 波動関数と角運動量の大きさ
スチーム さんのレス (2008/07/15(Tue) 19:53)
メントスさんの微分計算がまちがっているようです.もう一度チェックしてみてください. もちろん極座標で表示できることも大切です.
Re: 波動関数と角運動量の大きさ
メントス さんのレス (2008/07/15(Tue) 21:25)
返信ありがとうございます.
極座標でやってみました.
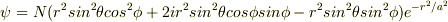
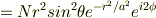
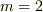 の,
の, 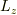 に対する固有関数が出てきました.
しかし,邪魔な係数があります.それと,mは分かりましたが,lが分からないです.
に対する固有関数が出てきました.
しかし,邪魔な係数があります.それと,mは分かりましたが,lが分からないです.
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/15(Tue) 22:28)
> 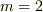 の,
の, 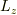 に対する固有関数が出てきました.
に対する固有関数が出てきました.
少なくとも,l>=mである事はわかります.この関数に 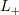 を作用させるとどうなるのでしょうか.以前のスピンの論議と似ていますが,すこし腰を落ち着けて,体系的に軌道角運動量を理解すれば,スピンとかアイソスピンなどでも驚かなくなると思います.
を作用させるとどうなるのでしょうか.以前のスピンの論議と似ていますが,すこし腰を落ち着けて,体系的に軌道角運動量を理解すれば,スピンとかアイソスピンなどでも驚かなくなると思います.
追加 >邪魔な係数があります.
これは何ですか?
Re: 波動関数と角運動量の大きさ
yama さんのレス (2008/07/16(Wed) 10:53)
を計算することによって
を求めることもできます.
いろいろな方法でやってみて同じ 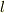 の値が得られることを確認しておくのがいいでしょう.
の値が得られることを確認しておくのがいいでしょう.
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/16(Wed) 12:00)
量子力学の本は手元にないので検索して見ました.下記の解説は,コンパクトにまとまってると思います.
h ttp://www.th.phys.titech.ac.jp/~muto/lectures/INP02/INP02_chap06.pdf
Re: 波動関数と角運動量の大きさ
メントス さんのレス (2008/07/17(Thu) 14:35)
>mNejiさん 係数というのは僕の勘違いでした.
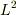 を作用させてみると,
を作用させてみると, 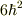 が出てきました.
よって,
が出てきました.
よって, 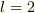 ということになります.
これも大学院入試の問題なのですが(言うのを忘れていてすみません.),この計算は楽ですけど,試験のときに極座標の
ということになります.
これも大学院入試の問題なのですが(言うのを忘れていてすみません.),この計算は楽ですけど,試験のときに極座標の 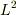 を導くのは大変かもしれません.
を導くのは大変かもしれません.
昇降演算子の式 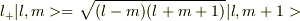 は割と簡単に導くことが出来ますが(というより,暗記しておくべきものなのでしょうか)
いまいちどのように使うのかが分かりません.
は割と簡単に導くことが出来ますが(というより,暗記しておくべきものなのでしょうか)
いまいちどのように使うのかが分かりません.
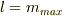 で
で 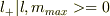 となるのは分かりますが,今の問題の場合はmの最大値が分からないので,どこまで演算子を作用させれば良いかが分かません.
今の場合だと,
となるのは分かりますが,今の問題の場合はmの最大値が分からないので,どこまで演算子を作用させれば良いかが分かません.
今の場合だと,  となります.
l=2だと,右辺が0になるから,答えはl=2ということで良いのでしょうか?
たまたまこの問題はmが最大値になっていましたが,mがlより小さいときは何かおかしくなるような気がします.
となります.
l=2だと,右辺が0になるから,答えはl=2ということで良いのでしょうか?
たまたまこの問題はmが最大値になっていましたが,mがlより小さいときは何かおかしくなるような気がします.
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/17(Thu) 15:27)
>いまいちどのように使うのかが分かりません.
> 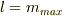 で
で 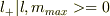 となるのは分かりますが,
となるのは分かりますが,
大雑把な説明しか出来ませんが,与えられた波動関数から,(l,m)の量子数を決める問題と捉えました.で角度依存性からゲスをしました.
1) m=2が判った段階で,l>=2まで判る訳ですが,内心l=2だろうと予測. というのも,θのノードが2だからです. 2) L+を作用すれば0となるだろう.この時は,面倒でも極座標の演算子L+を作用してゼロ.故に,m]max=2 -> l=2.
故に,与えられた波動関数の角運動量量子数(l,m)=(2,2)だろうと思う訳で.
なお,L+, L-はx,y表示でも,極座標表示でも覚え易いので,重宝します.
Re: 波動関数と角運動量の大きさ
メントス さんのレス (2008/07/17(Thu) 15:45)
mが先に分かっていて,そのときのlを求める場合,
(m'を与えられた数字だとします.)
この方法だと
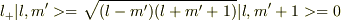 から常にl=m'となるわけですが,そうすると,与えられた波動関数のmが常に最大値を取ってることになりませんか?
例えば,m=2が与えられていても,l=3かもしれないし,l=4かもしれないと思うのですが,この方法だと常にl=m'になっているところが疑問に思います.
から常にl=m'となるわけですが,そうすると,与えられた波動関数のmが常に最大値を取ってることになりませんか?
例えば,m=2が与えられていても,l=3かもしれないし,l=4かもしれないと思うのですが,この方法だと常にl=m'になっているところが疑問に思います.
Re: 波動関数と角運動量の大きさ
yama さんのレス (2008/07/17(Thu) 17:39)
たとえば 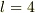 の場合は次のようになります.
の場合は次のようになります.
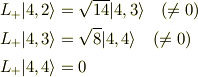
従って, 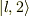 に
に 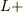 を1回作用させて0になれば
を1回作用させて0になれば 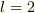 ,2回作用させて初めて0になれば
,2回作用させて初めて0になれば 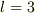 ,3回作用させて初めて0になれば
,3回作用させて初めて0になれば 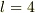 ,・・・であると言えるわけです.
,・・・であると言えるわけです.
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/17(Thu) 21:47)
この問題は;
(A)波動関数が 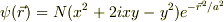 が与えられていて,この関数が軌道角運動量の固有値状態となるとすると,角運動量の量子数lとz座標への射影の量子数mを求める.
が与えられていて,この関数が軌道角運動量の固有値状態となるとすると,角運動量の量子数lとz座標への射影の量子数mを求める.
ことでは無いでしょうか.
ところが
>この方法だと
> 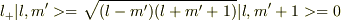 >から常にl=m'となるわけですが,
>から常にl=m'となるわけですが,
この論議が成り立つのは,軌道角運動量の完全基底となる固有関数群が既知のばあいの公式を持ち出されている訳です.
他方いまの問題では,この関数, 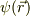 に演算子を作用させて
に演算子を作用させて
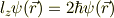
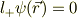
となったので,この関数, 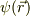 は,(l,m)=(2,2)の関数と考えられると主張している訳です.
は,(l,m)=(2,2)の関数と考えられると主張している訳です.
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
#追加説明
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
もし, 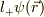 がゼロでないならば,
がゼロでないならば,

を確認し,そうならこの関数が,l=3かどうかを同様に検証する. 〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
勿論,yamaさんがご指摘のように,角運動量の自乗の演算子を計算して,その係数から,
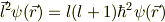
固有値「l」を求める事も出来ますが.何れにせよ,左辺の演算を実行して,その係数から固有値を決めることが必要と思います.
ここ数問のご質問を拝見していて感じるのは,具体的な問題で練習するよりは,「量子力学での軌道角運動量」の解説の流れを追っておかないと,大雑把な理解が育まれないかという点です.
とくに孤立系としての2体問題は,太陽と惑星の古典論から,水素と電子の量子論まで共通のイメージの問題です.ところが量子力学での角運動量は,角運動量の自乗と一つの射影だけが同時に決定出来るという不確定性を背負った物理量です.昔は,その点を歳差運動モデルで理解したと思いますが,最近ではどうなんでしょうね.
このイメージはある意味,量子力学の特徴を強く反映していると思います.その意味で,「量子力学での軌道角運動量」はじっくり勉強する甲斐があるのでは?
Re: 波動関数と角運動量の大きさ
メントス さんのレス (2008/07/17(Thu) 23:49)
ああ,勘違いをしていました.
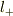 の場合でも,極座標表示で具体的に微分計算をするということですね.導出できるかどうか,やってみますので,ちょっと待ってください.
(自分でも他の方法をいろいろ考えてみたのですが,交換関係などを利用して抽象的に解く方法はないのですかね.)
の場合でも,極座標表示で具体的に微分計算をするということですね.導出できるかどうか,やってみますので,ちょっと待ってください.
(自分でも他の方法をいろいろ考えてみたのですが,交換関係などを利用して抽象的に解く方法はないのですかね.)
>「量子力学での軌道角運動量」の解説の流れを追っておかないと,大雑把な理 >解が育まれないかという点です. 一応,軌道角運動量については一通り勉強しなおして,自分なりに要点をまとめて把握したつもりなんです・・・. >その点を歳差運動モデルで理解したと思いますが,最近ではどうなんでしょうね. はい,ハイゼンベルグ運動方程式などで勉強しました.円錐が逆さまみたいになってるイメージ図ですよね.
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/18(Fri) 00:42)
>導出できるかどうか,やってみますので,ちょっと待ってください.
急ぐことはないと思いますが,逆に 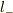 を逐次に演算して,m=1,0,-1,-2の波動関数を出しておくと,イメージが明確になると思います.
を逐次に演算して,m=1,0,-1,-2の波動関数を出しておくと,イメージが明確になると思います.
>抽象的に解く方法はないのですかね.
極座標表示での固有関数が球面調和関数である事を納得出来れば,良いだけですね.前回ご紹介したサイトのpdf(6.27式)の前後の論議が参考になるとおもいます.
>ハイゼンベルグ運動方程式などで勉強しました.
ハイゼンベルグ表示が得意なら,上記pdfの行列表示を先に見てから,球面調和関数表示をご覧になると簡単かも知れません.
追記 >円錐が逆さまみたいになってるイメージ図ですよね.
そうです.学生の頃,歳差運動の周期はどうなるのかで悩んだ記憶があります.
Re: 波動関数と角運動量の大きさ
nomercy さんのレス (2008/07/18(Fri) 00:57)
コメントですが
慣れてくると,
自然と 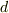 軌道(あるいは
軌道(あるいは 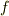 軌道)くらいまでは頭に入っているもので,
軌道)くらいまでは頭に入っているもので,
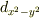 と
と 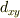 の重ね合わせだから
角運動量の大きさは2であるというくらいはすぐに分かるようになります.
の重ね合わせだから
角運動量の大きさは2であるというくらいはすぐに分かるようになります.
しかし,最初は地道に微分を計算してみて下さい.
Re: 波動関数と角運動量の大きさ
メントス さんのレス (2008/07/19(Sat) 11:38)
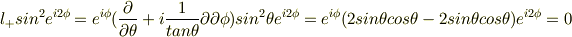
とたしかにゼロになりました. ありがとうございました.
>極座標表示での固有関数が球面調和関数である事を納得出来れば,良いだけですね.
>自然と 軌道(あるいは 軌道)くらいまでは頭に入っているもので
それは,球面調和関数の具体的な形をある程度覚えているということですか?
mNejiさんに紹介していただいたページでもそうでしたが,球面調和関数が 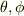 に依存していて,角運動量のz成分が作用する部分は
に依存していて,角運動量のz成分が作用する部分は 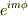 ということまでは覚えていたのですが,
ルジャンドル陪関数のほうの具体的な形までは,昔に教科書で見た程度で覚えていませんでした.
あと,聞きそびれていたのですが,ノードって何ですか?
ということまでは覚えていたのですが,
ルジャンドル陪関数のほうの具体的な形までは,昔に教科書で見た程度で覚えていませんでした.
あと,聞きそびれていたのですが,ノードって何ですか?
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/19(Sat) 11:55)
>とたしかにゼロになりました.
御芽出度うございます.一生この事は忘れないでしょう.
>それは,球面調和関数の具体的な形をある程度覚えているということですか?
私は「猫さんの記憶力」のオーダですから,特殊関数辞典(小型の)を頻繁に見ていました.でも,nomercyさんのおっしゃる通り,問題を解こうとしている近傍の関数形は,一時的には覚えていたと思います.
>ノードって何ですか?
波動関数の節点の意味のnodeです.波の固有状態がフラットならノードは0個ですし,両端が自由端の第一励起準位のノードは1個ですね.今回のノードは2個です.
#追記(2008-07-19 14:00頃) #量子力学波動関数だけでなく古典的波動にも言えることですね.私は,ファインマンさんが「ドラムを叩いている写真」を連想してしまいます. #波の絶対値がゼロとクロスする点と言った方が解り易いかも知れませんね.
恐らく,古い教科書には正確な説明があったと思うものの,物理の本はほとんど処分した現在,知る由もありません.私の感では,nomercyさんからお話をお聞きできると思いますが....
Re: 波動関数と角運動量の大きさ
nomercy さんのレス (2008/07/19(Sat) 12:29)
球面調和関数は覚えていませんでしたが, これを線形結合して実関数にした 立方調和関数の方はある程度覚えています. 例えば l=2 では
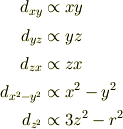
です.
Re: 波動関数と角運動量の大きさ
メントス さんのレス (2008/07/19(Sat) 14:03)
私は記憶するのが苦手なのですが,なんとなくの形を頭の片隅に入れておきます. というか,今回この問題を質問させていただいたことで,たぶんもう忘れないだろうと思います. 立方調和関数というのは,何かの本でみました.たしか,化学系のほうでよく使われるそうですね. お答えくださり,ありがとうございました.
Re: 波動関数と角運動量の大きさ
mNeji さんのレス (2008/07/19(Sat) 14:16)
nomercyさん,
>立方調和関数の方はある程度覚えています.
化学の「sp混成軌道」とかで,「p_x, p_y, p_z」なども立方調和関数だった訳ですね.その理解があれば,もう少し有機化学も楽しめたかもしれません....