古典統計を使える温度
古典統計を使える温度
メントス さんの書込 (2008/07/13(Sun) 02:32)
またまたお願いします. 他の掲示板でも聞いたのですが,解決せず,以前ここで質問させていただいた内容にも関連するので,こちらで質問させていただきます.
フェルミ分布が,古典統計に近似できる条件についてなのですが
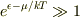 のときフェルミ分布の分母の1は無視できて
のときフェルミ分布の分母の1は無視できて
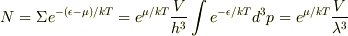 となるので
最初の条件
となるので
最初の条件 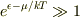 は
は 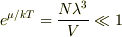 というふうに書き換えることができます.
ドブロイ波長
というふうに書き換えることができます.
ドブロイ波長  は温度に関係するので,温度をつかって条件を書くと
は温度に関係するので,温度をつかって条件を書くと
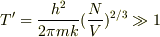 と書くことができます.キッテルの本によると,普通の場合は濃度が固定されているので温度が重要になる.とあり,
私は,上の式の温度より高温ならマクスウェルボルツマン統計,低温ならフェルミ統計をつかうと理解していました.
しかし,エネルギーギャップ
と書くことができます.キッテルの本によると,普通の場合は濃度が固定されているので温度が重要になる.とあり,
私は,上の式の温度より高温ならマクスウェルボルツマン統計,低温ならフェルミ統計をつかうと理解していました.
しかし,エネルギーギャップ 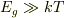 の十分低温で,真性半導体のホール密度を求めよという問題において,解答は低温にもかかわらずボルツマン統計を使っていました.
自分の理解のどこが間違っているのでしょうか?
の十分低温で,真性半導体のホール密度を求めよという問題において,解答は低温にもかかわらずボルツマン統計を使っていました.
自分の理解のどこが間違っているのでしょうか?
Re: 古典統計を使える温度
メントス さんのレス (2008/07/13(Sun) 16:13)
nomercyさん,ありがとうございます.
なるほど.基準となる温度は粒子密度に比例するので,真性半導体の場合はとても低くなるということですね.
しかし,それならば,真性半導体はいつでもマクスウェルボルツマン分布で扱って良いことになりませんか?
すると, 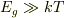 という条件を課したのはどういう意味があるのでしょうか?低温でマクスウェル分布が使えるなら,高温でも使えるはずなので温度の条件は特に必要ない気がするんです.
という条件を課したのはどういう意味があるのでしょうか?低温でマクスウェル分布が使えるなら,高温でも使えるはずなので温度の条件は特に必要ない気がするんです.
Re: 古典統計を使える温度
メントス さんのレス (2008/07/14(Mon) 14:05)
なるほど!粒子密度が十分少ないということをいうための条件だったのですね. 理解しました.
それでは,「系の温度が 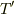 (これはおおよそフェルミ温度と同じと考えても良いのでしょうか?)より高温であれば,
(これはおおよそフェルミ温度と同じと考えても良いのでしょうか?)より高温であれば, 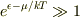 なのでフェルミ分布はマクスウェル分布で近似できる.」ということは理想気体に限らず,すべてのフェルミ粒子,ボース粒子(半導体や他の固体など)について成り立つと考えて良いのでしょうか?
なのでフェルミ分布はマクスウェル分布で近似できる.」ということは理想気体に限らず,すべてのフェルミ粒子,ボース粒子(半導体や他の固体など)について成り立つと考えて良いのでしょうか?
Re: 古典統計を使える温度
nomercy さんのレス (2008/07/14(Mon) 20:10)
であれば
であり,マクスウェル分布になるというのはその通りと思います.
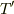 がフェルミ温度,というのはどうでしょうか?
金属の場合はおおよそフェルミ温度のよう(係数はちゃんと見てないが)ですが,
半導体の場合にはそもそもフェルミ温度の定義をどうするかという問題もあると思いますが.
がフェルミ温度,というのはどうでしょうか?
金属の場合はおおよそフェルミ温度のよう(係数はちゃんと見てないが)ですが,
半導体の場合にはそもそもフェルミ温度の定義をどうするかという問題もあると思いますが.
Re: 古典統計を使える温度
メントス さんのレス (2008/07/14(Mon) 21:25)
金属の電子が自由電子だとすると
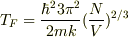 ですから,係数は違うけれど,オーダーとしては同じくらいだと思います.
たしかに,他の物質の場合はフェルミ温度がどうなるのか分かりません.
ですから,係数は違うけれど,オーダーとしては同じくらいだと思います.
たしかに,他の物質の場合はフェルミ温度がどうなるのか分かりません.
この問題を調べるときに,いろいろな教科書を読んでみたのですが,「フェルミ温度より高温ならば,古典領域.フェルミ温度より低ければ縮退が強い」というようなこと(フェルミ温度を基準としている.)を書いているものが多かったような気がします.
しかし,フェルミ温度が自由電子の場合でないと簡単に求められないのならば
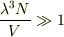 から得られた温度を基準にしたほうが便利なのではないのか,と思ったんです.つまり,
から得られた温度を基準にしたほうが便利なのではないのか,と思ったんです.つまり, 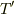 より高温なら古典領域,低温なら縮退が強い.ということです.こちらの条件は,フェルミ分布の式だけから導出したので,かなり一般的だと考えました.(ボース粒子のときも成り立ちますし.)
問題を解くときにはあまり関係のないことなので,どうでもいいことかもしれませんが・・・.
より高温なら古典領域,低温なら縮退が強い.ということです.こちらの条件は,フェルミ分布の式だけから導出したので,かなり一般的だと考えました.(ボース粒子のときも成り立ちますし.)
問題を解くときにはあまり関係のないことなので,どうでもいいことかもしれませんが・・・.
Re: 古典統計を使える温度
nomercy さんのレス (2008/07/14(Mon) 22:07)
を温度の基準に用いるのは別に構わないと思います.
多くの文献で,フェルミ温度が尺度として用いられることが多いことについて,私見を述べます.
フェルミ温度(エネルギー)や,フェルミ面あるいはフェルミ運動量というのは絶対零度において,非常に明快な物理的意味を持ちます.
例えば,フェルミエネルギーは絶対零度において粒子数分布 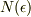 が不連続になる点と言えます.
(実は,自由粒子だけでなく,多くの金属においてこの事実は成り立つ)
このように,明快な物理的意味を持つ量なので,多くの文献で基本的な量として扱われていると考えます.
が不連続になる点と言えます.
(実は,自由粒子だけでなく,多くの金属においてこの事実は成り立つ)
このように,明快な物理的意味を持つ量なので,多くの文献で基本的な量として扱われていると考えます.
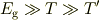
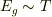 となると,
となると,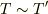 となる可能性があります.
となる可能性があります.