分子の速度，慣性モーメント

home > 掲示板 >

このページのPDF版

サイトマップ

分子の速度，慣性モーメント

digi さんの書込 (2008/07/12(Sat) 03:28)

(1)温度がおなじとき，水素分子の平均の速さは窒素分子の何倍か？

(2)球殻の慣性モーメントはどうやって求めるのでしょうか？

関連性のない質問で申し訳ありません． (1)は答えが√7となっているのですが，どう計算しても√14にしかなりません．

Re: 分子の速度，慣性モーメント

mNeji さんのレス (2008/07/12(Sat) 12:56)

digiさん，

（１）どのような式を元にそのように考えたかを示されると，コメント出来るとおもいます．

（２）球殻を《「球殻の外径と等しい外径の球」ー「球殻の内径と等しい外径の球」》と考えるとどうですか．

Re: 分子の速度，慣性モーメント

digi さんのレス (2008/07/12(Sat) 23:40)

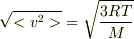(1)についてですが，分子の平均の速さは $\sqrt{<v^2>}=\sqrt{\frac{3RT}{M}}$ で表わされますよね？（Mは気体の分子量，Rは気体定数，Tは温度）求める値は

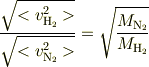
$\frac{\sqrt{<v_{\mathrm{H_2}}^2>}}{\sqrt{<v_{\mathrm{N_2}}^2>}}=\sqrt{\frac{M_{\mathrm{N_2}}}{M_{\mathrm{H_2}}}}$

となり，水素の分子量は2，窒素の分子量は28と考えて，答えは√14としました．

(2)は，半径a，質量Mのピンポン玉の慣性モーメントを求めるもので，球殻の厚さは無視するものとすればどうすればいいでしょうか？《「球殻の外径と等しい外径の球」ー「球殻の内径と等しい外径の球」》では0になる気がするのですが？

Re: 分子の速度，慣性モーメント

mNeji さんのレス (2008/07/13(Sun) 00:28)

（１）ああ，そうですね．原子番号と原子量とを勘違いしていました．お説で正しいと思います．

（２）ということは，面密度から定義に従って計算するしか無いように思います．球殻の中心を原点として，z軸について回転させると考えて慣性能率を定義に従って計算するのはどうですか？

Re: 分子の速度，慣性モーメント

mNeji さんのレス (2008/07/13(Sun) 11:09)

（２）に付いて補足

「球慣性モーメント」で検索すると；

一様な球の慣性モーメント

http://www14.plala.or.jp/phys/mechanics/35.html

というサイトを拝見出来ました．此処では球の慣性能率を密度と半径の関数として表現してあります；

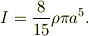
$I=\frac{8}{15}\rho\pi a^5.$

今，密度一定として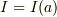， I=I(a) と考えます．すると，半径a〜a+δの薄い球殻の慣性能率をΔIとしますと；

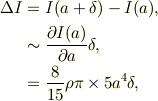
$\Delta I &= I(a + \delta ) -I(a),\\&\sim \frac{\partial I(a)}{\partial a}\delta,\\&= \frac{8}{15}\rho\pi\times 5a^4 \delta,$

となります．いま薄い球殻の質量をMとすると；

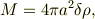
$M=4\pi a^2\delta\rho,$

の関係から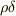， $\rho \delta$ を消去すれば，薄い球殻の慣性能率を求める事ができますね．

Re: 分子の速度，慣性モーメント

ｋｏｍａｇａｔａｋｅさんのレス (2008/07/15(Tue) 13:01)

慣性モーメントについての質問は多いですね．分かりにくいようです．

結局，意味が分からなくて公式に頼る事になってしまうからでしょう．面倒な積分の計算だけになります．

普通は剛体の回転についての運動方程式Ｉｄω／ｄｔ＝Ｎで定義されています．どれもなじめない量です．

私は運動エネルギーで考えるのがいいのではないかと思っています．自分で変形できますので公式に頼る度合いが少なくなります．イメージも取りやすいです．

半径ｒの円周上を角速度ωで運動している質量ｍの質点を考えます．速さｖ＝ｒω 運動エネルギー＝(1/2)ｍｖ^２＝(1/2)ｍ(ｒω)^２です．どちらの表現でも同じです．

質量が分布していればどうなるでしょうか．基本的には各部分についての重ね合わせで考える事になります．その場合，ｖの式ではなくてωの方の式を使います．ωが全体で1つ決まっていてもｖは各場所によって変わります．ｒが変わるからです．質量が分布している剛体に対してはｖを使うことが出来ません．

運動エネルギーを (1/2)Ｉω^２と表します．このＩが慣性モーメントです．質点の場合Ｉ＝ｍｒ^２です．質量が分布していてもｒが同じであれば同じ式です．ｍは全質量の意味になります．亜鈴型や円環もこの場合に当てはまります．

※円環の場合は面倒な計算なしで求まリます．積分は必要ありません． ※普通の力学の教科書では，棒，直方体，円板，球，・・・と進むようです．円環とか，球殻は円板，球の微分で考えるという立場からか後回しになっています．

半径がｒの円板は円環の重ね合わせです．（難しくありませんからやってみてください．）

半径の小さい所にも質量が分布していますから運動エネルギーは (1/2)ｍ(ｒω)^２よりも小さくなります．Ｉ＝αｍｒ^２でα＜１です．これは半径が(√α)ｒの円環に全ての質量が分布している場合と同じだということです．(√α)ｒは回転のエネルギーについての有効半径だと考えていいでしょう．慣性モーメントの計算はこのαを求めるものです．この同じＩが回転のトルクを考える時にも出てくるのです．

円板についての計算の結果はα＝1/2ですから有効半径はｒ／√２≒０．７ｒです．半径が０．７ｒの円環上に全質量のある回転と同じだということになります．

球殻も円環の重ねあわせで考えることが出来ます．今度はα＝３／４です．１／√２よりも少し大きいです．回転半径が球の半径に近い所のウエイトが大きいということになります．半径＝ｒ，高さ＝ｒの円筒（缶詰の缶のような形）の回転と半径ｒの球殻の回転とが同じになると言うともっとイメージが取れるのではないでしょうか．