ゆと さんの書込 (2008/07/09(Wed) 20:19)

大学２年電気電子工学科にて電磁気を学んでいます．質問ですが，「原点を中心とする，それぞれの外半径・内半径がaとｂ(a<b)の２重導体A・Bがある．導体球A・Bにはそれぞれ＋Q −２Qの電荷を与える．このときの電界を求めよ」という問題です． 僕は，半径rの球を閉曲面として任意に取り，?r<a?a<=r<=b ?b<rの３通りについて半径rの球表面で電界を積分すると考えました．このとき導体球Aの表面には，＋Qの電荷が表面に分布し，導体球Bでは導体内部の電界を打ち消すために，導体球Bの内部には−Qの電荷が，導体球Bの外表面には−Qと＋Qの電荷が分布するので?・?の場合は電界が０で?の場合はガウスの定理より「Ｅ＝Ｑ/２πεｒ」を得ると考えました．これらの考えは間違っていますか？解説お願いします．よろしくお願いします．大学で用いている教科書は「電磁気学ノート著：藤田広一」で，その他自分で「詳解電磁気学演習」「電磁気学著：二村忠元」等を調べましたが，あまり納得できない状況です．

mNeji さんのレス (2008/07/09(Wed) 21:10)

ゆとさん，初めまして．

導体Bには「真電荷＝-2Q」が有るのですね．そして導体Bの内側には導体Aからの誘導電荷＝-Qがある訳ですから，導体Bの表面電荷は「真電荷＝-2Q」+「-内側の誘導電荷 = -(-Q)」= -2Q + Q = -Q，となるような気がします．

ゆと さんのレス (2008/07/09(Wed) 21:50)

>導体Bの内側には導体Aからの誘導電荷＝-Qがある 僕が考えていたのは「−２Ｑの半分（つまり−Ｑ）が導体球Ａの＋Ｑに引きつけられるような形で導体球Ｂの内側に分布する」なのですがそうではないということですか？もしそうだとしたら，電界は外側にも生じ，同様にガウスの定理から「Ｅ＝−Ｑ/2πεｒ」となりますかね？ もう一つ質問があります．記事Ｎｏ．２０７６０の「半径rの球を閉曲面として任意に取り，?r<a?a<=r<=b ?b<rの３通りについて半径rの球表面で電界を積分する」というガウスの定理を用いる時の記述は第三者に十分に伝わりますか？

mNeji さんのレス (2008/07/09(Wed) 23:03)

＞僕が考えていたのは「−２Ｑの半分（つまり−Ｑ）が導体球Ａの＋Ｑに引きつけられるような形で導体球Ｂの内側に分布する」なのですがそうではないということですか？もしそうだとしたら，電界は外側にも生じ，同様にガウスの定理から「Ｅ＝−Ｑ/2πεｒ」となりますかね？

金属での真電荷は表面にのみ存在が許されますね．若し金属内部に電荷分布が有ればその近傍に電場が存在してしまいます；電荷に関するガウスの微分形式;

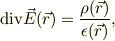
が有るからですね．

他方，この問題のように球対称である有限厚の球殻Bでは，真電荷とは独立に誘導電荷が内側と外側に発生しますが，内外の誘導電荷の和は中性条件に規定されるのでゼロです．

此処までが，電磁気の初歩の考え方です．電荷に関するガウスの積分形式

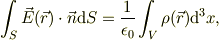
を考えれば，誘導電荷をいちいち考えなくとも，領域ごとに電場を与えられますね．勿論，電荷が球対称である限り，面積分を半径rの積分に書き下したり，体積分を電荷量に書き下すのは自由だと思います．

その意味では，導体Bの外側の半径も与えている方が考え易いと存じます．

＃ヒョットして導体Bは薄い球殻の設定ですかね． ＃それでも，裏と表は有りますよ．

なんとなく さんのレス (2008/07/10(Thu) 17:11)

横から失礼． ゆとさんの疑問点は以下の3点ですね． (1) 導体Ｂの内外（殻）の電荷はいくらか． (2) ガウスの定理により求めた答えは正しいか． (3) ガウスの定理を球表面の電界を積分する，という表現は正しいか． mNejiさんとかぶりますが，少し付け加えます． (1) 導体Ｂの外殻（球表面）電荷は-Qです．これはmNejiさんが説明されている通り，または，半径rを大きくとれば，その中にある”真”電荷は+Q（球Ａ）+(-2Q)（球Ｂ）=-Qからも出てきます．したがって，r>Bなる外ではこの真電荷による電場を計算しなければなりません． (2) 答えそのものが間違っています．球面の積分では球対称性から全方向に角度依存性がなくなります．このとき動径方向以外の（角度）寄与分は４π（ステラジアン）です． (3) 球面では面方向ベクトル，電場が常にともに動径方向のため，たまたま一致します．そのため，正確ではないですが，この場合は正しい答えを与えます．