大学院入試問題
大学院入試問題
スーザン さんの書込 (2008/07/07(Mon) 22:02)
ある大学院入試問題を解いていて,よく分からないところがありました.
永久双極子モーメントpをもった有極性の気体(温度T)がある.この気体に電場Eが加わると,割合として分子全体の pE/3kT が電場の方向を向くことを示せ. kはボルツマン定数である.
どなたかご教授願えますでしょうか?
Re: 大学院入試問題
mNeji さんのレス (2008/07/08(Tue) 00:37)
スーザンさん,初めまして.
電場が双極子モーメントに印可された時のエネルギはどのように表現されますか?またあるエネルギをもつ確率は温度の関数としてどのように表現されますか?
Re: 大学院入試問題
スーザン さんのレス (2008/07/08(Tue) 03:25)
mNejiさん
>電場が双極子モーメントに印可された時のエネルギはどのように表現されますか? エネルギU=-p・Ecosθ
>またあるエネルギをもつ確率は温度の関数としてどのように表現されますか? 確率P=exp(-U/kT)
であると思いますがいかがでしょうか? 上から求めたい割合がpE/kTに比例することは分かるのですが,1/3がどこから来るのか,それが不明です. exp(-U/kT)=exp(pE/kT)≒1+pE/kT が何か関係しますでしょうか?
Re: 大学院入試問題
mNeji さんのレス (2008/07/08(Tue) 10:34)
温度が高い程バラバラな角度をもち,とても高温では平均はゼロになると思います.その逆で,低温では....
>エネルギU=-p・Ecosθ
すると,Uはθの関数ですね.角度が大きくなるとエネルギは大きくなりますか,それとも?また角度θを変化させると,Uはどのように変化しますか?U=U(θ)とすると微分の知識が適用できるのでは.
>確率P=exp(-U/kT)
いま欲しいのは,U〜U+ΔUの範囲にある確率ですよね.
Re: 大学院入試問題
なんとなく さんのレス (2008/07/08(Tue) 10:55)
これは,やはり温度T>>0,つまり高温での極限で成立します. 問題は電場方向(Z軸にとる)への配位数ですので,単純に言えば ∫Cε(θ)exp(-pEcosθ/kT)dV/∫Cexp(-pEcosθ/kT)dV つまり,エネルギーε(θ)=pEcosθを取る状態の(ボルツマン)平均でよいと思います.
Re: 大学院入試問題
スチーム さんのレス (2008/07/08(Tue) 15:08)
>割合として分子全体の pE/3kT が電場の方向を向くことを
ここ「は高温でのcosθの期待値がpE/3kT となることを」
と書いたほうが良いようです.なんとなくさんの表現で,
∫cosθexp(-pEcosθ/kT)dV/∫exp(-pEcosθ/kT)dV dV=2πsinθdθ (0<θ<π)
Re: 大学院入試問題
mNeji さんのレス (2008/07/10(Thu) 08:53)
ご質問が途絶えているようなのですが,説明を進めてみます.
双極子モーメントが電場によって作る内部エネルギU=-p・Ecosθは,スチームさんのご指摘のように,0<θ<πの範囲で考えれば,角度とともに増大し,-pE<U<pEと変化します.
そこで,このような双極子モーメントがN_0個,温度T(K)で電場Eのもとに熱平衡している時には,その内,N個からN+dN個がエネルギU〜U+dUを持つとすれば,確率密度の温度依存性を考慮して,
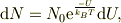
と表せます.
従って,内部エネルギ,Uの関数である物量量,f(U)の期待値(平均値)としては;
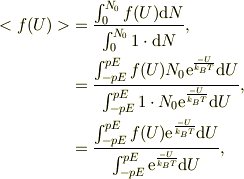
と表せます.
内部エネルギの期待値が必要なら,f(U)=U,とすれば良いですね.
【追伸】<U>を計算してみましたが,予想と違う結果になりました.ご専門の方からのご意見を戴けると,幸いです.計算ミスが有りそうですが,その結果は;
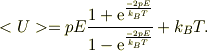
でした.
Re: 大学院入試問題
スチーム さんのレス (2008/07/10(Thu) 17:10)
計算は合っていると思います. 後,高温近似すれば設問の答えと一致します. と,思ったのですが,二つの項のどちらかの符号が違うのかも. 第一項の符号が逆ですね.
Re: 大学院入試問題
mNeji さんのレス (2008/07/11(Fri) 00:13)
>第一項の符号が逆ですね.
そうですね,指数関数を分母・分子で整理する時に符号を間違えた様です.しかし,そうしても,
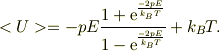
指数部が十分に小さい;
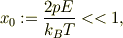
すなわち,熱エネルギの撹乱が双極子エネルギも大きければ,すなわち高温近似ならば,
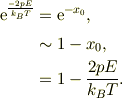
高温近似でのエネルギは,
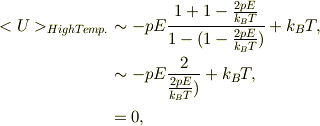
となりました.高温近似では,熱撹乱が大きく,全ての方向余弦を向く事が等確率で起こり,エネルギの平均値がゼロとなっている,ように思われます.
この高温近似での平均的な余弦量, 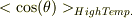 とすれば,
とすれば,
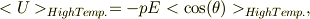
を満たすので,
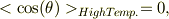
となる.高温近似では,熱撹乱が大きく,全ての方向余弦を向く事が等確率で起こり,平均値がゼロとなっている,ように思われます.
#これは題意より示された「ファクタ3」と合致しない...?
逆に低温近似を考えて見ます;
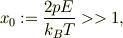
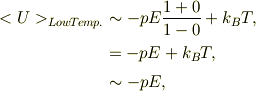
これは,低温の為に,ほとんど最低エネルギに落ちていて,電場の方向に全てのダイポールが配向していると見なせるとおもいます.
Re: 大学院入試問題
なんとなく さんのレス (2008/07/11(Fri) 02:15)
>mNejiさん
高温での近似は, <U>=-pE{(1+exp(-2x))/(1-exp(-2x))-1/x}(∵x=x0/2=pE/kT) ですが,これは, <U>=-pE{coth(x)-1/x} なので,x<<1 のcoth(x)のテイラー展開 coth(x)=1/x+x/3-x^3/45+・・・ を用いて,<U>〜-pE(pE/3kT)となります.つまり,近似の方法が間違っています. 分数の場合,各項を十分にとり,オーダーを合わせねばなりません.
Re: 大学院入試問題
mNeji さんのレス (2008/07/11(Fri) 03:04)
なんとなくさん,
><U>=-pE{coth(x)-1/x} なので,x<<1 のcoth(x)のテイラー展開 >coth(x)=1/x+x/3-x^3/45+・・・ >を用いて,<U>〜-pE(pE/3kT)となります.つまり,近似の方法が間違っています.
ご教示感謝致します.tanh(x)の展開は手元に在ったのですが,coth(x)の初項が1/xとは思いにも依りませんでした.
後で,見る方のために,参考サイトを書いておきます.
すると,
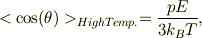
従って角度は,90°より少し前方となる,と考えられるのでしょうか.
Re: 大学院入試問題
スチーム さんのレス (2008/07/11(Fri) 09:59)
近似をあやまるとおかしな結果となりますが, 積分の前に指数関数を近似しておくと容易に結果がでます.
x.exp(ax)〜x(1+ax)=x+ax^2
積分すると (1/2)x^2+(1/3)ax^3
xの自乗の項は消えてしまいます.
Re: 大学院入試問題
mNeji さんのレス (2008/07/11(Fri) 10:36)
スチームさん,
>近似をあやまるとおかしな結果となりますが, >積分の前に指数関数を近似しておくと容易に結果がでます.
この手の問題を自力で解こうとしたのは始めてです(門前の小僧とか).双曲線型関数は正負で展開項が打ち消し合ったりするので,いつもの積もりで一次の展開で打ち切りをしていたのが悪いと思いませんでした.
それにしても「統計」の振る舞いは不思議ですね.どう解釈すればいいのやら....