教えて さんの書込 (2008/07/03(Thu) 23:55)

プールで伏し浮きの姿勢をとり，プールサイドをけったとする．このとき足には反作用の力が働く．今度は，プールサイドから離れたところで同じように足で水をけったとする．それぞれの場合で反作用の力の大きさは違うだろうか．違うとしたらどうしてか？ すみませんが，詳しく教えていただきたいです．お願いします．

mNeji さんのレス (2008/07/04(Fri) 00:31)

プールサイドは，人間が足で蹴っても，変形もしないし，質量も十分にあるので動きもしません．従って蹴った力の反作用の結果として，抗力は100%の大きさで逆向きの方向に推進出来ます．

他方，足で水を蹴ると，水は容易に変形しながら，かつ水は粘性抵抗(摩擦力の一種)を示す為に足の運動エネルギを吸収してしまうので，蹴った力の反作用の結果としては，抗力の大きさは100%の大きさにはなりませんが，逆向きの方向への推進力を生じます．

【追記と修正：2008-07-04 09:45】

yama さんのレス (2008/07/04(Fri) 01:37)

mNejiさんの説明では作用と反作用の大きさが等しくないようにも受け取れますが，作用と反作用の大きさは常に等しくなるはずです．すなわち，次の関係が成り立ちます． プールサイドを蹴る力＝プールサイドから受ける反作用 水を蹴る力＝水から受ける反作用 しかし プールサイドを蹴る力＞水を蹴る力 なので プールサイドから受ける反作用＞水から受ける反作用 ということになります．

anon さんのレス (2008/07/04(Fri) 09:32)

## 書き込みのタイトルとお名前は適切に > 元質問者のかた

問題は二つあって， > 力の大きさは違うだろうか．違うとしたらどうしてか？ でした．

> しかし
> プールサイドを蹴る力＞水を蹴る力
> なので，

これは一つ目の問題についての回答ですね．

残る問題は，どうして プールサイドを蹴る力＞水を蹴る力 となるのかということですね．

運動エネルギを吸収してしまうという説明だと， エネルギーの話から力の話に繋がる因果関係が見えないですよね． 設問として「どうしてか」という文言なので， 因果関係の説明が求められているのだと思います． エネルギーと力の繋がりは，本当は因果関係ではないのだという世界観を会得するのは， なかなか難しいですね．

（追記） ↓mNejiさんのご説明に反論したようなつもりではなかったのですが... 私が書いたのを読み直してみましたが， ひょっとして「なかなか難しいですね」というところを， 「mNejiさんにとってはなかなか難しい」といっていると思われたのかなぁ... そんなつもりはまるでなくて，誰にとって難しいのかというと， 一般的に難しいことだろうなというつもりで，しいて言うなら， 元の質問者の方「教えて」さんにとって難しいことだと思った といえないこともないですが．

mNeji さんのレス (2008/07/04(Fri) 10:08)

anonさん，

＞運動エネルギを吸収してしまうという説明だと， ＞エネルギーの話から力の話に繋がる因果関係が見えないですよね．

それでは，「因果関係」をご説明願えませんか？

粘性流体固有のエネルギ散逸過程が根底にあるので，力学的な運動を引き出す力が発生した時に，その反力が出て来ると感じます．完全流体ならば，反力(反作用の力＝抗力)＝ゼロです．

＞エネルギーと力の繋がりは，本当は因果関係ではないのだという世界観を会得するのは， ＞なかなか難しいですね．

では，どんな関係なのでしょうか？というよりも何をご主張になっているのか理解出来ませんので，もう少し砕いてご説明願えると幸いです．

toorisugari no Hiro さんのレス (2008/07/04(Fri) 10:28)

> 完全流体ならば，反力＝ゼロです．

本当にそうですか? ダランベールのパラドックスは等速度で移動する物体に対しての議論であって，加速度のある物体に対しては成り立たないと思いますが．

mNeji さんのレス (2008/07/04(Fri) 10:47)

＞ダランベールのパラドックスは等速度で移動する物体に対しての議論であって，加速度のある物体に対しては成り立たないと思いますが．

では，どれほどの寄与が有るのでしょうか？

ｋｏｍａｇａｔａｋｅ さんのレス (2008/07/04(Fri) 10:51)

私は プールサイドを蹴る力＝水を蹴る力 として考えるのがいいのではないかと考えています． 足の働かせ方としては同じものを考えているはずです． Ａ，Ｂ２つの物体の間に縮めたバネを置いた時と同じではないでしょうか． 人だと蹴るという足の動かし方と反動で動く時に受け取る力の感じがごっちゃになりますので原動力としての力は一定という条件をイメージするのはバネの方がいいように思います．

(Ａ)(バネ)(Ｂ)

Ａに着目します（Ａが人です）．ＢがどういうものかによってＡの動きは変わってきます． Ｂは硬いとします． Ｂの質量が大きいほどＡの飛び出しの速さは大きいです．Ｂの質量が小さければＡの飛び出しの速さは小さくなります．

Ｂがやわらかい場合はどうなるでしょう． 力が加わると変形する，流れるということが起こります． 色々議論があるでしょうが大雑把には これは上の「Ｂが硬くて質量が小さい」場合と同じになるとしていいのではないでしょうか． 足にフィンをつけると進みやすくなるというのはＢの質量を大きくする工夫だという事になります．

toorisugari no Hiro さんのレス (2008/07/04(Fri) 12:29)

> では，どれほどの寄与が有るのでしょうか？

さあ？ 少なくとも > 完全流体ならば，反力＝ゼロです． といいきるのは考察不足かと．

非粘性流体でばた足などで水流が発生するのかどうか(非粘性のとき静水中で団扇を扇ぐと水流が発生するか?流体全体にある方向の運動量が付与されるか)，わかりません．(たぶん，ないでしょう．そういう意味ではmNejiさんの言明は正しいのですが．)

# 問題: # 非粘性静止流体中に，流体で満たした風船を入れ，栓を抜いた，ある大きさのところで栓が閉じるとする．風船は速度を持っているか?

しかし，粘性流体では確実にこれらの水流は発生しますし，このとき発生する力は粘性によってエネルギーが吸収されたために起こるのではなくのでなく(あるけど人間スケールでは微々たるものです)，力学的な作用反作用(運動量の人間から水への移動)です．

mNeji さんのレス (2008/07/04(Fri) 12:50)

toorisugari no Hiroさん，

ここで返答を保留したい所ですが，そうすると他の方に大きな誤解を生じると思うので，私見を書いてみます．

＞少なくとも ＞> 完全流体ならば，反力＝ゼロです． ＞といいきるのは考察不足かと．

逆に言えば，静止状態の運動初期には，「完全流体ならば，反力＝ゼロ」は第ゼロ近似で成立すると思います．

一般に，toorisugari no Hiroさんの論議は，大雑把な論議を終えてからの詳細部分を先頭に持って来るので，私の様な素人には理解が困難になります．もう少し，素人の段階での理解をアクティブにするようにして下さると幸いです．

＞風船の様にゴムの中に水が詰められた水を放出する場合は，非粘性流体でも加速度が発生するのは自明です．

これは流体に対する運動量の印加機構が「ゴム容器の体積収縮」であって，その放出部分の水の塊がゴム容器から噴射される「作用・反作用」に基ずくものであると思います．もしも容器の長さが長く，粘性が高ければ，噴出速度は遅くなる筈です．

＃【追加説明；2008-07-04 13:05】

＃完全流体を持ち出したのは，平たい「陸上」と平たい「氷上」での歩きを念頭にかいたものです． ＃前進できるには何らかの摩擦機構か，ロケットのような噴射機構か，直接の力の交換が必要です．

ご質問者さんには，そこまで細かい論議は，ぎゃくに混乱をまねくと考えます．

＞非粘性流体でばた足などで水流が発生するのかどうか，(非粘性のとき水の中で団扇を扇ぐと水流が発生するか)，わかりません．

此れなどは，どなたも論議していない様におもいます．

＞このとき発生する力は粘性によってエネルギーが吸収されたために起こるのではなくのでなく(あるけど微々たるものです)，力学的な作用反作用(運動量の人間から水への移動)です．

どうするとこのような考え方になるのか理解出来ません．私が行っているのは「流体中で流体を蹴るとエネルギ散逸機構が存在するのでその推進力は，流体中で十分に大きな固体を蹴るより，小さくなる」と言っている訳です．

toorisugari no Hiro さんのレス (2008/07/04(Fri) 13:04)

>> 風船の様にゴムの中に水が詰められた水を放出する場合は，非粘性流体でも加速度が発生するのは自明です．

これは消去しました．忘れてください．

「流体中で流体を蹴るとエネルギ散逸機構が存在するのでその推進力は，流体中で十分に大きな固体を蹴るより，小さくなる」

論理が変です．

「流体中で流体を蹴ると水流が発生して，反作用としての推進力を得る．しかし，粘性による抗力を受けるので，合力としての推進力は小さくなる」

ならわかります．しかし，これでも，「固体を蹴ること」との間に関係は見えないです．

単に，

プール壁は剛体で「無限」の質量があるので，力積 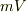の「キック」による質量 の人間の運動量の変化は 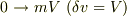だが，粘性流体に対してはすべての流体を運動させるわけではない，つまり，有限の質量相手なので，同じ力積のキックに対して速度変化が小さい ．

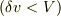どれだけの質量の流体を蹴り出せるか? それだけのはなしでしょう．

スチーム さんのレス (2008/07/04(Fri) 13:14)

komagatakeさん >>原動力としての力は一定という条件をイメージするのはバネの方がいいように思います

このところは出題と異なりませんか．むしろ原動力＝ける力が異なるのはどうしてかという疑問では．

ｋｏｍａｇａｔａｋｅ さんのレス (2008/07/04(Fri) 14:56)

スチームさん

＞このところは出題と異なりませんか．むしろ原動力＝ける力が異なるのはどうしてかという疑問では．

皆さん，こういう風に考えて議論しておられるのですか．

質問文の中には ＞同じように足で水をけったとする と書かれています．

同じように水を蹴っているのになぜ進み方がこれだけ違うのかという誰でもが感じる認識から出発しています． それを 「反作用が異なるからだ， 「作用と反作用は等しいはずだ，蹴った力が等しいのであれば反作用も等しいのではないか， 「なぜ反作用に違いが出てくるのだろうか と考えての質問ではないのでしょうか．

私は皆さんの議論が質問と違う所で行われているような気がしたのです． 間にバネを考えるということをやったのは出す力と感じる力を分離しようという目的からです．

人が力を加える時には反作用を確認しながら（足裏での感覚をフィードバックさせながら）行っています．「同じように蹴っているのに」という条件がなかなかうまく実現しなくなっています．原動力としての力と推進力として受け取る力とが感覚的にはうまく分離できません．

toorisugari no Hiro さんのレス (2008/07/04(Fri) 17:34)

> 前進できるには何らかの摩擦機構か，ロケットのような噴射機構か，直接の力の交換が必要です．

粘性がないとどちらの機構も機能しませんが，有限のしかし無視できる粘性の流体では「摩擦機構」はほとんど無視でき，「噴射機構」（というよりジェットエンジン）のみで考察されます．

ミジンコの遊泳を考えるときは「摩擦機構」が優勢ですが，人間の遊泳の場合1/100〜1/1000の影響しかありません．

ミュフ猫 さんのレス (2008/07/04(Fri) 18:59)

ロケット宇宙船の推進力は「噴射機構」ですよね？ 宇宙の粘性は無視できる有限値を持つのでしょうか？ 今まで 0 と思ってました．(^^;)

toorisugari no Hiro さんのレス (2008/07/04(Fri) 20:49)

もちろん0です, すくなくとも，われわれのスケールで観れば

ミュフ猫 さんのレス (2008/07/04(Fri) 21:49)

やはりそうですか． 横レス失礼しました．

mNeji さんのレス (2008/07/04(Fri) 23:22)

以下，纏めてコメントするので，区切り記号「〜〜〜〜」を使います．

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 No.20656で，yamaさん，

＞プールサイドを蹴る力＝プールサイドから受ける反作用 ＞水を蹴る力＝水から受ける反作用 ＞しかし ＞プールサイドを蹴る力＞水を蹴る力 ＞なので ＞プールサイドから受ける反作用＞水から受ける反作用 ＞ということになります．

しかし，これについては，

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 No.20662＆No.20668の，komagatakeさんと； 〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 No.20667で，スチームさんとの論議で，

＞同じように水を蹴っているのになぜ進み方がこれだけ違うのかという誰でもが感じる認識から出発しています．

というご意見をお持ちですが，私も似た感触もっています．例えば，地上で垂直ジャンプするのもプールサイドから水平ジャンプするのも，股関節と膝の屈曲→伸展の動作は同じだとおもいます．この場合，それらの関節を駆動する筋肉の出すトルク量は一定と近似できると思います．

水中での蹴りの場合も，股関節と膝の屈曲→伸展の動作は同じだとおもいます．すなわち脚の出力は同じはずなのに，推進力が大変に少ないという理由が求められていると思います．

私自身，まだこの点を上手く表現出来ませんが，地上の歩行で「静止摩擦力以内の推進力」では，人も車も前進出来ますが，駆動力が静止摩擦力を上回ると，人も車もスリップするのと似た事で説明出来るのだろうと推測しています．

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 No.20657で， anonさん，

(追記)を拝見しましたが，やはり良く判りませんでした．論議ですから，各自の見解を出し合うのがよろしいかと思います．

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 No.20666で，toorisugari no Hiroさん，

＞どれだけの質量の流体を蹴り出せるか? ＞それだけのはなしでしょう．

なるほど．しかし，もう一歩踏み込んで説明が欲しいですね．

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜 No.20669で，toorisugari no Hiroさん，

＞粘性がないとどちらの機構も機能しませんが，有限のしかし無視できる粘性の流体では「摩擦機構」はほとんど無視でき，「噴射機構」（というよりジェットエンジン）のみで考察されます．

特に「粘性がないとどちらの機構も機能しません」が何を指しているのか理解出来ません．

またジェットエンジンは酸化剤としての空気をターボファンによって収集・圧縮する点を除けば，基本的にロケットの噴射機構と同一と思っていました．

他方，掌を仰角90度で押し出す状態をプールで観察していると，手の甲に追跡している乱流の塊は気泡の混入から可視でき，全面から廻り込んだ流れが，後方の塊にトラップされながら，同時にすこしずつ後方に流れだすのが見えます．このプロセスは剪断力が有るからこそ発生できると思います．

yama さんのレス (2008/07/05(Sat) 01:08)

「同じように水を蹴る」というのは曖昧な表現でいろいろな解釈ができそうです． これを，「同じ力で蹴る」と解釈すれば，プールサイドからの反作用も水からの反作用も同じになるはずです． しかし，問題は同じ力で蹴ることができるかどうかです． プールサイドを軽く蹴るのだったら，同じくらいの力で水を蹴ることもできるでしょう．その場合，水を蹴るときに足を伸ばす速さは，プールサイドを蹴るときに足を伸ばす速さの何倍にもしないといけないでしょう． プールサイドを全力で蹴るのと同じ力で水を蹴るためには，その場合の足を伸ばす速さの何倍もの速さで足を伸ばさないといけないと思いますが，そんなことは不可能でしょう． 「同じように水を蹴る」というのを，「同じ速さで足を伸ばす」と解釈することもできると思います．この場合はもちろん同じ力で蹴ることはできません．

mNejiさんが示された例のように，人間が地面を蹴って走る場合，蹴る力（の水平成分）は最大摩擦力を超えることはできません． 摩擦係数の異なる２種類の地面があるとき，つまり滑りやすい地面と滑りにくい地面があるとき，両方の地面を同じ力で蹴れば，当然同じ反作用を受けます． しかし，滑りやすい地面の最大摩擦力よりも大きい力で滑りにくい地面を蹴るとすれば，それと同じ力で滑りやすい地面を蹴ることはできません， 大きい力で蹴ろうと努力しても足が後方に滑るだけで，蹴る力は最大摩擦力より大きくはなりません． 水を蹴る場合は，摩擦力の小さい地面を蹴る場合のように，大きい力で蹴ることは難しくなります．もちろん，最大摩擦力のようにはっきりした限界はないのですが，同じ力で蹴るために何倍もの速さで足を動かさないといけないので，蹴る力を大きくすることが難しくなるというわけです．

mNeji さんのレス (2008/07/05(Sat) 08:26)

yamaさん，

＞「同じように水を蹴る」というのは曖昧な表現

確かにこの問題はあります．でも，泳ぐ側の感覚では「プールサイドに足をつけて蹴る」と「臥し浮きから蹴る」のとで関節の駆動力を調整しているとは考えにくいです．

陸上での静止状態からの運動を考えれば，最大静止摩擦力以下の駆動力で動く限り純粋に運動エネルギだけの増加になります．ところが，それを越えた駆動力のもとではスリップしながらも動摩擦係数に従って運動する為に運動エネルギよりも熱エネルギの発生のほうが大部分になるとおもいます．決して摩擦係数の値に追従して駆動力が自動的に変化するとは思えません．

この事例は，「氷の上を歩く人」，「濡れていて滑り易いカーブを走行する車」で見る事が可能です．これらの場合，滑りにくい状況ではスリップしない駆動力でも，静止摩擦力を越える状況ではスリップし，その余剰エネルギが熱エネルギに転換している訳です．

＃自動車レースで，カーブを曲がる時に「ブレーキをかけながらアクセルを踏む」操作は， ＃わざとスリップをさせてスピンを起こし，速度が低下してブレーキが利いた後， ＃強い静止摩擦を利用して，スピンによる回転後の方向に再加速するような気がします．

水中では，最大静止摩擦力のようなドラスティックな閾値はありませんが，抗力係数の速度依存性という意味では，高速になるほど抵抗が低くなるという特性を示す訳です．その意味でも，駆動力を一定に保って動く場合，運動エネルギに転換出来ない余剰エネルギは「熱エネルギ」ないしは「流体の進行方向に垂直な方向への運動エネルギ」に転換されるのではないでしょうか？

やはり流体系の振る舞いを定性的にも取り入れた説明が望まれると思います．

yama さんのレス (2008/07/05(Sat) 15:06)

関節の駆動力のもとになるのは関節を動かす筋肉の収縮力だと思います． 筋肉の収縮力を意識して調整していないとしても，意識しなければ収縮力がいつも一定でであるとは言えないと思います． 負荷に応じて無意識的に収縮力は変化するのではないでしょうか． たとえば，平坦な道を歩く場合と，坂道を歩く場合は，足の筋肉の収縮力は違うと思いますが，意識して収縮力を変えているわけではないと思います．

自動車の場合，駆動輪に加わる力が最大摩擦力を上回る場合エンジンのする仕事の一部が熱になるのはその通りだと思います． その場合でも，駆動輪に加わる力がいつも一定であるとはいえず，たとえばエンジンの回転数や変速比によって変化すると思います．

泳ぐ場合に，筋肉の収縮による仕事の一部が熱エネルギーや水の運動エネルギーに変わるのその通りだと思いますが，足の筋肉の収縮力が，プールサイドを蹴る場合と同じだとは言えないと思います．

mNeji さんのレス (2008/07/05(Sat) 16:52)

なにか自動制御的な話になってきていると思います．簡単なモデル分析ですから，あまりに細かな条件付けには疑問を持ちますね．

＞泳ぐ場合に，筋肉の収縮による仕事の一部が熱エネルギーや水の運動エネルギーに変わるのその通りだと思いますが，足の筋肉の収縮力が，プールサイドを蹴る場合と同じだとは言えないと思います．

ですから，その理由を原理的な解釈をしたいとおもって考えようとしたわけです．

他方私は，クロールのモデルとして，「腕の関節運動により，掌を後方に向けて仰角90°で押す」ことで推進力すると仮定し，手の抗力係数の実験値，胴体全体の表面積に対する抗力係数の実験値を使って，速度・消費エネルギなどの計算をしようとしています．このような計算は実験値に基づいているだけで，流体力学的な解釈とはまだかけ離れているので，今回のご質問に興味を持った次第です．

私の次の段階では，クロールでの脚の推進モデルを数値流体力学的にシミュレートするつもりですが，さらにその次の段階で，平泳ぎの脚のそれに挑戦したいとおもっています．そこに至れば，脚の推進力がどのような流体力学的運動に転換されて行くかをシミュレートできるだろうと推定しています．

したがって， 逆にいえば，今の段階では理解不可能です，ご免なさい→ 教えてさん．

toorisugari no Hiro さんのレス (2008/07/05(Sat) 19:16)

> なるほど．しかし，もう一歩踏み込んで説明が欲しいですね．

どこがわからないか言ってくだされば，もう少しふみこめるかもしれません．

toorisugari no Hiro さんのレス (2008/07/05(Sat) 19:44)

>> 粘性がないとどちらの機構も機能しませんが，有限のしかし無視できる粘性の流体では「摩擦機構」はほとんど無視でき，「噴射機構」（というよりジェットエンジン）のみで考察されます．

> 特に「粘性がないとどちらの機構も機能しません」が何を指しているのか理解出来ません．

タンクにしきりを入れ，片方のタンクに圧力をかける(ロケット推進)か，水を注水するか(ジェット推進)し，しきりに小さな穴をあけると水流がもう一方のタンクに発生します．これはジェット(噴流)と呼ばれる現象で非粘性流体の枠組みで解析できます．(今井さんの教科書に載ってると思います)

ジェットエンジンは噴流により運動量を持つ流体を無限遠方へ放出することで推進力を発生させます．この現象が非粘性流体の枠組みで解析できると言うことは推進力そのものは粘性とは直接関係ありません．流れパターンのみで決まります．

しかし，このパターンが問題です．噴出口の前後では流れのパターンは非対称です．前方では四方から緩やかに流体が集合するのに対して，後方では平行な流れ(噴流)として離れていきます．

もし後方も四方に広がる流れなら，推進力は小さくなるでしょう．

ジェットエンジンの場合，前方では四方から緩やかに流体が集合し，後方で噴流として離れていきますが，後方でも四方に広がるなら，これはさらに前方に戻る事を意味しているので，ほとんど推進力は出ないでしょう．(運動量の無限遠方への輸送がない)

噴流という流れパターンが重要ですが，実は後方が噴流になる流れと後方も四方に広がる流れのどちらも非粘性流体の解となります．循環保存則で考えると四方に広がる流れが自然です．

噴流が発生するには「きっかけ」としての粘性が必要になります．境界層の剥離現象(流れが壁から離れること)です．境界層(剥離)がないと噴流は発生しません．ですから，完全に非粘性な流体ではジェットエンジンは機能しません．

これはロケットでも同じです． 以前の記事で 「非粘性流体中で風船ロケットは進むか」みたいな問題を出しましたが，もし，噴流が発生しないなら(境界層剥離が起こらないなら)，風船は速度を持ちません．

ミュフ猫 さんのレス (2008/07/05(Sat) 21:41)

なるほど． では，ロケット宇宙船の場合，「境界層の剥離現象」を引き起こす「粘性」は， どんな物質が持っているのでしょうか？

mNeji さんのレス (2008/07/05(Sat) 22:28)

toorisugari no Hiroさん，

＞どこがわからないか言ってくだされば，もう少しふみこめるかもしれません．

素人の悲しさは，判らない所が判らない事だと思います．

＞タンクにしきりを入れ，片方のタンクに圧力をかける(ロケット推進)か，水を注水するか(ジェット推進) し，しきりに小さな穴をあけると水流がもう一方のタンクに発生します．これはジェット(噴流)と呼ばれる現象で非粘性流体の枠組みで解析できます．(今井さんの教科書に載ってると思います)

色々とご教示くださり，有り難うございます．残念なことに，自分には上のお話はイメージすら出来ませんでした．

今井さんの本では「複素解析と流体力学」しか持っていません．流体力学の教科書としては神部さんの本と演習書とを持っていますが，ほぼ手つかずです．今回，ご説明戴いている「境界層とか粘性流」などの関連をイメージできるようになる為には，どの様な項目を勉強すればよろしいでしょうか？例示するには今井さんの教科書の目次でお教え戴ければ幸いです．本屋さんで見て，神部本の対応部分を眺めてから，全体を勉強する予定です．

yama さんのレス (2008/07/05(Sat) 22:47)

ジェットエンジンの場合の推進機構は単純ではないと思います． というのは，ジェットエンジンでは吸入した空気を圧縮した後，そのまま放出するわけではないからです． 吸入した空気で燃料を燃やすことによって気体が発生します． 吸入空気中の酸素の一部が燃焼によって二酸化炭素などに置き換わり質量が増加するとも言えます．また，燃焼によって気体の温度や圧力も変化します． これは，流体力学的には酸素の吸いこみと二酸化炭素の湧き出しが生じていると同時に温度や圧力の変化も起こっているということではないでしょうか？

スチーム さんのレス (2008/07/05(Sat) 23:03)

toorisugari no hiro さん >噴流という流れパターンが重要ですが，実は後方が噴流になる流れと後方も四方に広がる流れのどちらも非粘性流体の解となります．循環保存則で考えると四方に広がる流れが自然です．

これと

>タンクにしきりを入れ，片方のタンクに圧力をかける(ロケット推進)か，水を注水するか(ジェット推進)し，しきりに小さな穴をあけると水流がもう一方のタンクに発生します．これはジェット(噴流)と呼ばれる現象で非粘性流体の枠組みで解析できます．

の関係が今ひとつわからないところです．非粘性ではタンクの噴流は生じないという結論でしょうか．直感と異なりますが．

ミュフ猫 さんのレス (2008/07/05(Sat) 23:06)

なるほど． 単に，圧縮放出するのと，燃焼させて放出するのではメカニズムが違ってくる のですね． では，宇宙空間で，宇宙飛行士が船外作業をするとき，エアジェットランドセル みたいなものを背負いますよね？ あれは単に，ノズルから圧縮空気を噴出させて推進力を得ています． あれの場合，「境界層の剥離現象」を引き起こす「粘性」は，どんな物質が持 っているのでしょうか？

スチーム さんのレス (2008/07/05(Sat) 23:20)

すみません．話の流れをさえぎったようですが，私の疑問はミュフ猫さんと同様です．

>噴流が発生するには「きっかけ」としての粘性が必要になります．境界層の剥離現象(流れが壁から離れること)です．境界層(剥離)がないと噴流は発生しません．ですから，完全に非粘性な流体ではジェットエンジンは機能しません．

直感では，非粘性で噴流は生じるように思えます．

yama さんのレス (2008/07/06(Sun) 00:47)

燃焼させてから放出する場合も，推進力が生じるためには流れが物体表面から離れることは必要でしょう．

なお，非粘性流体の場合に噴流が生じるためには流れが物体から離れる必要があるとしても，それを境界層の剥離とは言わないのではないでしょうか？ 非粘性流体では境界層自体が存在しないと思います．

物体のまわりが空気で満たされている場合は，噴出された空気は，周囲の空気に邪魔されて自由に広がることができず，周囲の空気と混じり合って空気の流れをつくります．物体の表面に沿った流れも生じるので，その流れが物体表面から離れない限り噴流にはならないでしょう． しかし，宇宙空間のように物体のまわりが真空の場合は，噴出された空気を邪魔するものはなく，空気は自由に広がってゆくはずで，物体表面に沿った流れはできないでしょう． これが噴流と言えるかどうかはともかくとして，噴出された空気の反作用として推進力は生じると言えるでしょう．

toorisugari no Hiro さんのレス (2008/07/07(Mon) 13:07)

> なるほど． > では，ロケット宇宙船の場合，「境界層の剥離現象」を引き起こす「粘性」は， > どんな物質が持っているのでしょうか？

宇宙の場合，希薄気体であり，「流体」としてみれるかという問題がありますが，もし「流体」なら，燃料の液体燃料，液体酸素，燃焼生成物の混合ガスだと思います．

ただし，宇宙空間では，噴出口あたりは希薄すぎて「圧力」「粘性」という概念自体が成り立たないとは思います．

> ジェットエンジンでは吸入した空気を圧縮した後，そのまま放出するわけではないからです．

たぶん剥離がなければ，双極子流れ＋わき出し流れ，剥離があれば，噴流(＋一様吸い込み)＋わき出し流れの様になると思います． 等方的なわき出し流れでは推力はでないですよね．だから，今回は無視しました． (重ね合わせであらたな推力成分が出るかもしれませんが．．．)

> 非粘性ではタンクの噴流は生じないという結論でしょうか．直感と異なりますが．

非粘性流体では循環(速度の閉じた線績分=渦度の面積分)が保存します．つまり，渦なしの流れから渦度は発生しません．

ジェット解自体はラプラス方程式の解として，非粘性渦なし流体の一つのパターンです．しかし特異点をふくんでいます．これが問題です． (2次元ポテンシャル渦 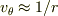も特異点が原点にあります．)

ジェットが発生するということはその界面に「渦度」が発生していることを意味します(界面に水車を置くと回転します)．上流の流れには渦度はありませんから，よって「循環」が発生していることになり，循環保存則に反します．つまり，「粘性」を取り入れるか，剥離点は循環保存則が破れる「非正規な点」と観るかの解釈が必要です．

ただし，剥離の部分(ノズルの端)と界面を無視すれば，のこりは非粘性でも取り扱えます．

> なお，非粘性流体の場合に噴流が生じるためには流れが物体から離れる必要があるとしても，それを境界層の剥離とは言わないのではないでしょうか？

非粘性流体では境界層自体が存在しないと思います．

もちろん，境界層は粘性流体での概念です．特異点をどう解釈するかの問題だと思いますが．

toorisugari no Hiro さんのレス (2008/07/07(Mon) 13:56)

> 物体の表面に沿った流れも生じるので，その流れが物体表面から離れない限り噴流にはならないでしょう． > しかし，宇宙空間のように物体のまわりが真空の場合は，噴出された空気を邪魔するものはなく，空気は自由に広がってゆくはずで，物体表面に沿った流れはできないでしょう． > これが噴流と言えるかどうかはともかくとして，噴出された空気の反作用として推進力は生じると言えるでしょう．

無限遠方で観たときに，ロケットの燃焼生成物が一方方向に推進しているなら，推進力は発生していますが，燃焼生成物が四方に広がっているのなら，推進力は発生してないですよね．

「非粘性」という仮定，「連続体」という仮定が成り立つとは思えませんが，もし，成り立つ場合，真空中でも「噴流」が発生するというのは自明でないのでは?

toorisugari no Hiro さんのレス (2008/07/07(Mon) 14:43)

>> どこがわからないか言ってくだされば，もう少しふみこめるかもしれません． > 素人の悲しさは，判らない所が判らない事だと思います．

粘性の話を忘れて，高レイノルズ数の世界でかんがえるなら，泳ぐと言うことは，手のひらなり足なりで，水をジェットとして後方に送り，その反作用で進むことです．そのとき掻き出されるの水の質量は， 手のひら等の断面積×ストローク長で評価できます．

おおざっぱには人間の体積程度の水しか掻き出せない，つまり，人間の比重と水の比重を同じと観れば，作用する質量は高々，自分の体重程度です．

壁を蹴ると質量は「無限大」です．

ある質量 を蹴って，質量 の人間が静止状態から速度 を持つ状態になるのに必要なエネルギーは

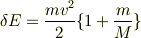
となります．エネルギー効率は違いますね．

# 力積で評価してましたが，yamaさんのおっしゃるとおりエネルギーで評価すべきですね．

>> (今井さんの教科書に載ってると思います) > 例示するには今井さんの教科書の目次でお教え戴ければ幸いです．本屋さんで見て，神部本の対応部分を眺めてから，全体を勉強する予定です．

今井さんの「流体力学(前編)」です．手元にないのでページはわかりませんが，死水理論あたりを読まれればいいのでは?

mNeji さんのレス (2008/07/07(Mon) 18:52)

＞非粘性の話を忘れて，高レイノルズ数の世界でかんがえるなら，泳ぐと言うことは，手のひらなり足なりで，水をジェットとして後方に送り，その反作用で進むことです．

これは，私が知る実験的事実と大きく異なっている様に思います．容器としてのプールに対して，プールの水は静止しています．人がプールを泳ぐというのは，その静止水に対して動く事でプール水から反作用を受けて体を推進する事です．体は全体的にプール水から摩擦力を受けて減速をします．

で，一つの問いは「手を動かす時に，静止水を手の運動方向に投げ出す事ができるか？」と言う事が出来ます．まさにロケットの噴流のように「水の塊」を前方向に投げるイメージでしょうか．これを考えていたころ，家の洗面場が平坦なステンレスであり，そこに水の噴流が衝突しているのに気付きました．私は，それまで，平面に衝突した水は跳ね返るものだと思っていたのですが，むしろ平面に衝突した水流は，同心円を描いて広がるだけでした．まさに完全非弾性衝突をしているようで，驚きました．

斜めに水流が入射すると，流石に有限の反射角で跳ね返るかとおもって，金属板で実験しましたが，これも駄目で，入射した水流は金属面に張り付く様に上方にも広がるのでした．

この洗面場は２Fにあるので，水圧が低くて流量がすくなからかと思い，地面にある車の側面に強い水流を垂直に流入させましたが，大雑把な振る舞いとしては楕円にちかい形で側面に張り付くのです．ただ，面から10°程度の浅い散乱も観察されますが，量は微量でした．

これは，水中の中での手の運動とは必ずしも同じ現象ではありませんが，少なくとも「水」と「固体面」との相互作用は意外とマクロな段階でも有意な大きさを示すと考えるようになってきました．

そこで，お風呂場で，手を動かす時にどのような水流がでるかを写真にとることにしました．掌を前面としてゆっくり動かして，水面の模様を観察しました．この模様からは，掌の前面に指2本程度の盛り上がりが出来て，それらが側面から斜め後方に広がり，さらに手の甲の側で，渦を形成しながら手の甲に追従しているのが確認されています．

これらの実験的事実を組み合わせてみると，静止水から掌は「ニュートン流的な運動量を受けることは在っても」，水流は掌に「ほぼ完全非弾性的衝突」をする為に前方に向けてジェットを形成出来ないで，掌面に沿って広がると推定しています．

その代わりに「手の甲の裏側に生成される後方渦群の塊」を，前方に投げ出す事は可能です．これはバタフライの手の動きの様に空気を巻き込んだ場合，掌側の泡は容易に離脱するものの，手の甲の裏側に付いた泡は，手の甲の運動に追従してトラップされる事から，可視化できています．すなわち，手を直線的に動かした後に，手首を前腕と真直ぐなままに，肘を中心に円運動をさせると，後方渦にトラップされている気泡群が手の長さ(〜20cm)程前方に出て行くことが観察されるからです．

という訳で，ご説明の現象は事実に反する様に感じます．

toorisugari no Hiro さんのレス (2008/07/07(Mon) 19:39)

> その代わりに「手の甲の裏側に生成される後方渦群の塊」を，前方に投げ出す事は可能です．

符号の違う渦対(あるいは3次元なら渦輪)は，短いジェットとおなじものですが．．．．

ミュフ猫 さんのレス (2008/07/07(Mon) 20:25)

yamaさん，toorisugari no Hiroさん， 返信レスありがとうございました．m(_ _)m 直感的には理解できた気がします．ｗ

mNeji さんのレス (2008/07/07(Mon) 21:39)

＞符号の違う渦対(あるいは3次元なら渦輪)は，短いジェットとおなじものですが．．．．

タバコの煙で，リング状の放出が出来たとおもいますが，あれはリングの近傍にのみ分布していて，そのリングの内部の部分は動いていない様に思いますが．

それに対して，飛行機の翼の上面の効果の説明； ・空気の「スコップ」としての翼：図9翼のスコップ

• http://home.comcast.net/~clipper-108/lift-J2.pdf

を拝見していると，翼の下面よりも上面の効果が大きいというのと類似していると推察されます．

恐らく，手の甲の後方塊は，動的な「手の甲のスコップ」として水のバルクな塊を加速しながら放り出せると感じています．といったモデル化をする為に，流体力学を勉強したいのですよ．

yama さんのレス (2008/07/07(Mon) 23:24)

空気中のロケットについて考えてみました． 次のような単純化したモデルを考えます． 圧縮空気を入れた中空の球の一部に穴を開けて空気を噴出させます， ジェットエンジンと違って空気の吸入は行われないので，空気の流れは一方的です．すなわち噴出した空気が戻ってきて再び穴から吸い込まれることはなく，放出された空気および周囲の空気の流れは最終的には無限遠に向かうはずです． 従って非粘性気体であっても球面に沿った流れはどこかで球面から離れないといけません． 実際，穴から出て球面に沿って流れる空気は，球面上で穴の反対側のところまでくると，球面に沿って逆向きに流れてきた空気と衝突します．そうなるとそのまま進むことはできないので，空気の流れは必然的に球面から離れることになります． その結果，穴から出た空気はあらゆる方向に広がることになりますが，穴から出る瞬間には，噴出空気全体としては穴から外に向かう運動量を持っているはずです．従って球は逆向きの運動量を得ることになります． つまり，空気中でも推進力がはたらくことになります．

もちろん，このモデルは水泳にはあてはまりませんが．

mNeji さんのレス (2008/07/07(Mon) 23:54)

＞空気中のロケットについて考えてみました． ＞次のような単純化したモデルを考えます．

素人としては，このような場面は，流体力学というよりは分子運動論として見れば，定性的には推進出来るのが明白だとおもいますが...．

他方，流体力学で「粘性流」と「固体面に静止」とが組み合わさって出て来ると，未だ分子運動論的な描像と乖離が多くて，狼狽えてしまいます．

toorisugari no Hiro さんのレス (2008/07/08(Tue) 08:33)

> タバコの煙で，リング状の放出が出来たとおもいますが，あれはリングの近傍にのみ分布していて，そのリングの内部の部分は動いていない様に思いますが

(太さのある)一巻きコイルに電流を流したときの磁場と，速度場は同じです．

mNeji さんのレス (2008/07/08(Tue) 10:47)

＞(太さのある)一巻きコイルに電流を流したときの磁場と，速度場は同じです．

そのイメージだと，手をコイルの面に対応させると，速度場は手の甲から掌を抜けているのでしょうか．

以前，インターネット上で拝見したのですが，「大小の渦輪が正面衝突すると，相互に通り抜けた」様なうろ覚えが有ります．

また，自分の手の観察では，後方渦は手を急に止めると「手の甲に衝突」しますし，前回ご紹介したように，肘を中心に回転運動をさせると「手の甲に衝突せずに，前方に進む」ようです．

toorisugari no Hiro さんのレス (2008/07/08(Tue) 10:57)

> その結果，穴から出た空気はあらゆる方向に広がることになりますが，穴から出る瞬間には，噴出空気全体としては穴から外に向かう運動量を持っているはずです．従って球は逆向きの運動量を得ることになります． > つまり，空気中でも推進力がはたらくことになります．

初期には移動するけど，噴出が終わったら止まってしまうことはないですか?

四方に空気が出ていくと，いずれ，前の方にも回り込んで「電気双極子」(「磁気双極子」ではなく)のような速度場になるとみているのですが．

# 磁気双極子(一巻きコイルの磁場)なら運動量があると思いますが，速度場のrotは非零つまり，コイルのあたりに渦が発生しています． # 電気双極子の速度場のrotは零ですね．

toorisugari no Hiro さんのレス (2008/07/08(Tue) 11:04)

> 以前，インターネット上で拝見したのですが，「大小の渦輪が正面衝突すると，相互に通り抜けた」様なうろ覚えが有ります．

はい，たしか教科書にも演習問題があったような．

> また，自分の手の観察では，後方渦は手を急に止めると「手の甲に衝突」しますし，前回ご紹介したように，肘を中心に回転運動をさせると「手の甲に衝突せずに，前方に進む」ようです．

急に止めると逆向きの力積を与えることになりまし，手を途中で消すことはできないので，「抜き手をする」か「スナップを利かせる」などの処置が必要となります．

> そのイメージだと，手をコイルの面に対応させると，速度場は手の甲から掌を抜けているのでしょうか

手が動いていることをお忘れなく．追いかけているのです．

yama さんのレス (2008/07/08(Tue) 12:23)

>初期には移動するけど，噴出が終わったら止まってしまうことはないですか?

噴出が終わると推進力はなくなりますが，それまでに得た運動量が失われることはないと思います．

>四方に空気が出ていくと，いずれ，前の方にも回り込んで「電気双極子」(「磁気双極子」ではなく)のような速度場になるとみているのですが

前方に回り込んだ空気が，そこで再び吸入されるならば，双極子のような速度場ができるでしょう．ジェットエンジンの場合はそうなりそうです．ただし，磁気双極子ですが． 吸い込み口と湧きだし口がつながっていなければ，電気双極子型の速度場になるでしょうね． しかしロケットでは前方に回り込んだ空気は吸入されることなく表面から離れていくと思います．従って速度場はどちらのタイプの双極子のようにもならないと思います，

toorisugari no Hiro さんのレス (2008/07/08(Tue) 12:31)

えっと，風船のように，空気を放出しながら縮んでいく「ロケット」を非粘性(循環保存則が成り立つ)流体中で放したら，運動量が発生するかという問題ですよね．

> しかしロケットでは前方に回り込んだ空気は吸入されることなく表面から離れていくと思います．従って速度場はどちらのタイプの双極子のようにもならないと思います，

前方に回り込んだ流体はそのまま縮む風船に追従して，風船の消失点めがけて集中する流れができるように思いますが．

それとも，縮まないで，空気だけ放出する(わき出しのある)モデルをお考えでしょうか?

たぶん，電気双極子+単極子のような速度場になるだけだとおもいます．

yama さんのレス (2008/07/08(Tue) 12:51)

実際のロケットは風船のように縮むことはないので，私は中空の金属球に圧縮空気をつめたようなものを想定しました． その場合穴から出て前方に回り込んだ空気は（吸入されるのではなく）合流して表面から離れ，前方に流れていくと思います． 単極子に似ている点もありますが，湧き出しは等方的ではなく運動量を持ちます． また，湧き出し口が球の外部にあるのではなく，球にくっついていることも重要です． そのため球は湧き出しと逆向きの運動量を得るわけです．

mNeji さんのレス (2008/07/08(Tue) 13:35)

＞> 以前，インターネット上で拝見したのですが，「大小の渦輪が正面衝突すると，相互に通り抜けた」様なうろ覚えが有ります． ＞はい，たしか教科書にも演習問題があったような．

そうですか，その教科書をぜひとも拝見したいです．思い出された時で結構なのですが，お教え下さると嬉しく存じます．

＞> また，自分の手の観察では，後方渦は手を急に止めると「手の甲に衝突」しますし，前回ご紹介したように，肘を中心に回転運動をさせると「手の甲に衝突せずに，前方に進む」ようです． ＞ ＞急に止めると逆向きの力積を与えることになりまし，手を途中で消すことはできないので，「抜き手をする」か「スナップを利かせる」などの処置が必要となります．

これも平泳ぎの手の動きは，実際にそうしているのだと思います．水泳では，流体力学的な説明を強く否定する事が多く，私の様に「水泳の素人」が言っても，理解してくれません(泣)．今度，論議する機会があれば，このご説明を引用してみたいと思います．

＞> そのイメージだと，手をコイルの面に対応させると，速度場は手の甲から掌を抜けているのでしょうか ＞手が動いていることをお忘れなく．追いかけているのです．

始めに引用した「渦輪」のばあい，その生成時には固体面と接しているのでしょうが，生成後は自由空気空間を渦輪のみが等速的に進行していた様に感じていましたが．

それとも，手の場合(仮に掌だけと仮想的に簡易化するとして)，動きながら渦輪を連続的に作り出しているようにイメージするのでしょうか．

渦輪のシミュレーションを拝見した記憶がありますが，どうしてもダイナミックな挙動というより，スタティックな特性を示す様な気がします．あまり先入観にとらわれ過ぎかもしれませんが...．

# ただ空気中の渦輪のレイノルズ数は，水泳の手のレイノルズ数に比べて1/10と考えれば，空気の動きが柔にみえても良いのかも知れませんね．

何れにしろ，流体力学の教科書を早めに読破して，CFDに手を出すべきな状況との認識を強く感じます．自分なりに判るのはいつの事か知れませんが，その時には，このスレッドにご報告したいと思います．

私の質問は，一応終了とさせて頂きます．ご質問者の方，ご回答者の方々との論議，有り難うございました．

toorisugari no Hiro さんのレス (2008/07/08(Tue) 14:25)

> それとも，手の場合(仮に掌だけと仮想的に簡易化するとして)，動きながら渦輪を連続的に作り出しているようにイメージするのでしょうか．

ストロークが短ければ手の平から外に出た流れ(渦層)が巻き込み渦輪を形成すると思います．十分にストロークが長いと管状の渦層になり不安定性により，複数の渦輪あるいは乱流状態になるのではないかと．

スナップを利かせたとき，どのような渦構造(毛糸の編み物様?)になるのか興味があります．

toorisugari no Hiro さんのレス (2008/07/08(Tue) 14:35)

> その場合穴から出て前方に回り込んだ空気は（吸入されるのではなく）合流して表面から離れ，前方に流れていくと思います． > 単極子に似ている点もありますが，湧き出しは等方的ではなく運動量を持ちます． また，湧き出し口が球の外部にあるのではなく，球にくっついていることも重要です． > そのため球は湧き出しと逆向きの運動量を得るわけです．

ここまでいくと，もはや計算するしかなさそうですね．簡単のため，2次元で計算するとして，円柱表面にわき出しをつけて，円柱表面の全面積力を計算すると0か否か?．．．．．

非浸透条件のため，円柱内部にもわき出しと吸い込み，あるいは双極子を置かなければいけませんが．．．．

わき出しの特異点あたりの圧力計算が難しそう．

yama さんのレス (2008/07/08(Tue) 16:04)

穴の周辺では流速が大きいため圧力が低く，合流点付近では流速が小さくなって圧力が高くなるでしょう． そのため，表面の全面積力は空気が噴出する向きにはたらくでしょう． しかし，噴出する空気からの反作用もはたらきます．

これらの力全体の大きさを計算することは難しいと思いますが，運動量を考えることによって力の向きは決まると思います． 球面に沿って前方に向かう流れもありますが，流れ全体としては噴出する向きの運動量を持つため，球は逆向きの運動量を持つことになると思います．

mNeji さんのレス (2008/07/08(Tue) 16:33)

＞スナップを利かせたとき，どのような渦構造(毛糸の編み物様?)になるのか興味があります．

次のページ；(1243) drain MtSPH2D おふろの排水（マルチスレッド版）

• http://mike1336.web.fc2.com/app/j1201_1250/1243_drainMtSPH2DP/drainMtSPH2D.html

は，とても示唆的で，一時は毎日眺めていました．このJava Appletの手法をまねっこして，水泳の解析をしたいのですが，その為にも，流体力学を学ばねばならないというジレンマに落ち入っています．

この数値計算は，風呂のそこから出て来た噴流が平面に衝突して広がるモデルとしてみる事が可能です．よく見ると，完全非弾性衝突ではなくで，微小角ながら反発を示している事が気になる所です．

このサイト「分子のおもちゃ箱」は，オーナの mike(みけ，と読むらしい)さんの物理感が溢れているユニークで美しいものです；

• http://mike1336.web.fc2.com/index.html

が，同時に数値計算の醍醐味を堪能出来る事例が満載です．

私としては，渦糸モデルよりは粒子法的な渦モデルみたいな方向に進みたい所です．どのみち，これらの数量計算手法も，近似すべき流体力学も共に判らないのがお恥ずかしい所です．

現在は，これに平行してプールでの観察と，小型ロクロに，金魚のエア・ストーンという発泡する道具を用いて定量的な観察とを進めようと思っています．

toorisugari no Hiro さんのレス (2008/07/08(Tue) 21:53)

> 球面に沿って前方に向かう流れもありますが，流れ全体としては噴出する向きの運動量を持つため，球は逆向きの運動量を持つことになると思います．

これは計算していないのでなんともいえません．

もし，噴出をやめてもロケットが移動しているのなら，つまり運動量を獲得しているのなら，反対符号の運動量を進行方向と逆の無限遠方に輸送している部分があるはずです．

しかし，yamaさんの流れは十分遠方でみると等方な「わき出し」にすぎません．進行方向と逆の方向に運動量を輸送しているようには見えません．仮に輸送しているのだとしても，渦双極子(渦輪)の様な特異点を放出しているのでない限り，噴射をやめれば運動量輸送は消え，物体も止まるように思います．

# 7/9 日本語を修正し，蛇足を消しました．

yama さんのレス (2008/07/09(Wed) 00:27)

十分遠方では流れは等方的に見えるかもしれませんが，厳密に等方的ではなく，等方性からの僅かなずれが流れ全体の運動量を生じるのではないかと思います． もちろんきちんと計算したわけではないので，厳密な計算で流れ全体の運動量が0になる可能性は否定できませんが・・・．

もし，湧き出しが止まった瞬間に球が運動しているなら，球はそのときの速度で動き続けると思います， なぜならその瞬間には，球は静止した非粘性流体中を動いているわけですが，非粘性流体中を等速度で動く球には抵抗力がはたらかないので減速することはないからです．

toorisugari no Hiro さんのレス (2008/07/09(Wed) 00:53)

> なぜならその瞬間には，球は静止した非粘性流体中を動いているわけですが，非粘性流体中を等速度で動く球には抵抗力がはたらかないので減速することはないからです．

初期は流体もロケットも静止していたはずです．運動量保存則はどうなるのでしょう．

yama さんのレス (2008/07/09(Wed) 14:37)

確かに，運動量の保存則からは流体が静止すればロケットも静止することになりますね． どうやら，気体を非圧縮性流体のように取り扱ったのが適切でなかったようです． 非圧縮性流体であれば，噴射を始めた瞬間に流体全体に流れが生じ，噴射が停止した瞬間にすべての流れが停止します． しかし実際には，ロケットの噴射気体も空気も圧縮性の流体です． 噴射された直後は密度が高く，急速に膨張しながら噴射口から遠ざかっていきます． また噴射を停止した瞬間に全体の流れが止まることもありません．流れの変化が音速を超えて伝わることはないからです． 従って噴射を停止してもすぐにロケットが停止することはありません． しかしロケットが動いていると，周辺の空気密度の変化が生じ，その変化が周囲に伝わります．つまり音波となって放射されるわけです．その造波抵抗のためロケットはだんだん減速するでしょう．

もちろん，実際は空気には粘性があるので，粘性抵抗のほうが大きいと思いますが．

toorisugari no Hiro さんのレス (2008/07/09(Wed) 14:52)

> どうやら，気体を非圧縮性流体のように取り扱ったのが適切でなかったようです．

ということは， 「 非粘性(循環保存=流れの剥離なし)・非圧縮・静止流体中でわき出しロケット(短時間噴射)は運動量を獲得できない． 」 でよろしいのでしょうか?

yama さんのレス (2008/07/09(Wed) 20:31)

そのように言えそうですね． ただし，何か見落としている論点があるかも・・・．

toorisugari no Hiro さんのレス (2008/07/09(Wed) 21:14)

> ただし，何か見落としている論点があるかも・・・．

私もそう思います:-)

わき出しのon/offなんて変ですし，たぶん圧縮性を考えないといけないでしょうね．(ま，ゆっくりやればごまかせそうですが．)

ともかく，渦が生成されないと，抗力や揚力だけでなく，推力も発生しないのじゃないかと言うのはかなり確信に近くなりました．

おつき合いいただいてありがとうございました．