電磁波の運動量を求めるためのモデル
電磁波の運動量を求めるためのモデル
メントス さんの書込 (2008/07/01(Tue) 00:04)
完全導体の反射を考えることによって,電磁波の運ぶ運動量を求めるという面白そうな問題なのですが,途中で行き詰ってしまいました.
問題
求める手順として,平面電磁波が表面の平らな完全導体で反射されるときに導体の受ける圧力を求め,その圧力によって生じる力積が電磁波の運動量変化に対応するとして運動量を求める.
導体表面に原点をとり,入射波の進む向きをz軸,電磁波成分の向きをx軸にとると,入射平面波の電場成分は 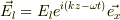 で表される.(
で表される.( 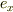 はx方向の単位ベクトルです)また,導体表面はz軸に垂直とする.(xy面が導体表面です.)
1,完全導体表面で反射する反射波の電場成分を求めよ.
2,入射波と反射波をあわせた波の電場成分を求めよ.
3,入射波と反射波をあわせた波の磁場成分を求めよ.ただし,
はx方向の単位ベクトルです)また,導体表面はz軸に垂直とする.(xy面が導体表面です.)
1,完全導体表面で反射する反射波の電場成分を求めよ.
2,入射波と反射波をあわせた波の電場成分を求めよ.
3,入射波と反射波をあわせた波の磁場成分を求めよ.ただし, 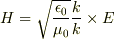 である.
4,上の磁場成分によって導体表面に現れる電流密度を求めよ.
5,この電流が磁場と相互作用して導体に力を及ぼす.発生する圧力の一周期についての平均値を求めよ.
6,単位体積あたりの運動量を求めよ.
である.
4,上の磁場成分によって導体表面に現れる電流密度を求めよ.
5,この電流が磁場と相互作用して導体に力を及ぼす.発生する圧力の一周期についての平均値を求めよ.
6,単位体積あたりの運動量を求めよ.
自分の解答
1, 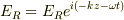 z=0での境界条件から
z=0での境界条件から 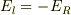 よって,
よって, 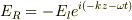 2,
2, 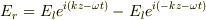
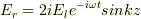 (x成分)
3,
(x成分)
3, 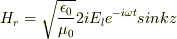 (y成分)
4,マクスウェル方程式から
(y成分)
4,マクスウェル方程式から 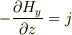 から
から
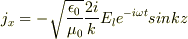 5,ローレンツ力の式
5,ローレンツ力の式 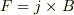 で,4のjと3のHは直交しているから
で,4のjと3のHは直交しているから
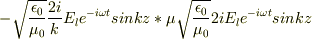
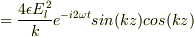 となったのですが
細かいファクターの計算間違いなどはあるかもしれませんが,とにかく
時間に依存する項が
となったのですが
細かいファクターの計算間違いなどはあるかもしれませんが,とにかく
時間に依存する項が 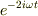 という振動項のみのため,一周期で積分すると,圧力が0になってしまいます.
どこかに見落としがあるのでしょうか.
よろしくおねがいします.
という振動項のみのため,一周期で積分すると,圧力が0になってしまいます.
どこかに見落としがあるのでしょうか.
よろしくおねがいします.
Re: 電磁波の運動量を求めるためのモデル
mNeji さんのレス (2008/07/01(Tue) 01:45)
自分に取っては超うろ覚えですが,大雑把なコメントをさせて頂きます.
- 電磁場ともに導体の外では,入射波と反射波の重畳ですよね.
- 導体内部での電流は,電場の入射波成分が侵入した結果の電場により,オームの法則,
 により与えられる方が自然な気がします.
により与えられる方が自然な気がします. - 導体内部での電磁波は,導体内部に向かって進行しながら電流を発生する為に,減衰する波動方程式,これを何と言ったか忘れましたが,に従ったと思います.これは,表面だけで直ぐに減衰してしまうと仮定しても良いかも知れません.いずれにしろモデル依存ですね.
- z=0で,導体内部と導体外部の接線方向の成分が連続するという協会条件に従う筈ですね.
- 圧力は進行波についての運動量密度ベクタ,
 から求められたように思います.(定義がうろ覚えですが)
から求められたように思います.(定義がうろ覚えですが)
といったシナリオだったような気もします.
(砂川 重信・著,理論電磁気学 初版を勉強したのですが,今手元に有りません.同著者の「電磁気学の考え方」には出ていません.)
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/01(Tue) 15:02)
電流が存在するのは,導体鏡面(z=0)だけなので,一般のzについてFを求めても意味がありません. ところがメントスさんの式でz=0と置くとF=0になります.つまり1周期で積分しなくても力は常に0ということになります.
これは3.で求めた磁場成分が正しくないためだと思います.
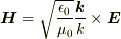 の関係を用いる場合,入射波と反射波では
の関係を用いる場合,入射波と反射波では 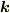 の向きが反対であることに注意しないといけません.
従って,入射波と反射波についてそれぞれ別々に
の向きが反対であることに注意しないといけません.
従って,入射波と反射波についてそれぞれ別々に 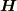 を求めてそれらを重ね合わせる必要があります.
上記の関係式を用いると,反射波の
を求めてそれらを重ね合わせる必要があります.
上記の関係式を用いると,反射波の 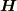 はz=0では,入射波と同じ向きになることが分かります.これはz=0で入射波と反射波の電場の向きが反対になるのとは対照的ですね.
入射波と反射波の重ね合わせによって定常波ができますが,z=0は電場波では節,磁場波では腹になるわけです.
はz=0では,入射波と同じ向きになることが分かります.これはz=0で入射波と反射波の電場の向きが反対になるのとは対照的ですね.
入射波と反射波の重ね合わせによって定常波ができますが,z=0は電場波では節,磁場波では腹になるわけです.
また,ローレンツ力の計算も正しくないように思います.
導体表面では, 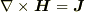 が成り立ちますが,この関係によると
が成り立ちますが,この関係によると 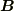 が逆向きになると
が逆向きになると 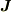 も逆向きになるので,ローレンツ力
も逆向きになるので,ローレンツ力 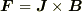 は常に同じ向きになることが分かります.従ってそれを平均しても0にならないことは明らかです.
は常に同じ向きになることが分かります.従ってそれを平均しても0にならないことは明らかです.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/02(Wed) 00:15)
>mNejiさん ありがとうございます. ですが,このモデルにそって解かなければならない問題なんです. 理論電磁気学は私もこの問題を調べるときに参照しました. 完全導体の反射は載っていたのですが,運動量のことまでは触れていなかったように思います.
>yamaさん
ありがとうございます.
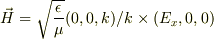 で計算すると,
で計算すると,
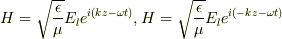 が出てきて,合成すると
が出てきて,合成すると
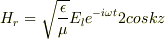 となって,たしかにz=0の境界面で腹になりました.
しかし,ここでzで微分し,電流密度を求めると
となって,たしかにz=0の境界面で腹になりました.
しかし,ここでzで微分し,電流密度を求めると
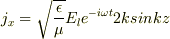 となり,z=0の導体表面で電流は0になってしまいます.
(一番最初の記事と同じになりましたが,どうやら,最初に計算間違いをしていたみたいです.)
Fは常に同じ向きになるということは,どこかで振動項が打ち消しあって消えてしまうはずということでしょうか.
となり,z=0の導体表面で電流は0になってしまいます.
(一番最初の記事と同じになりましたが,どうやら,最初に計算間違いをしていたみたいです.)
Fは常に同じ向きになるということは,どこかで振動項が打ち消しあって消えてしまうはずということでしょうか.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/02(Wed) 01:22)
導体内部の磁場は0なので,磁場はz=0で不連続になりますね.
磁場が不連続なところでは, 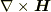 は普通の関数としては存在しませんが,δ関数を用いて表すことができるでしょう.
表面にだけしか電流が存在しなければ,電流密度がδ関数で表されるのは当然です.これをz=0を含む微小区間で積分すれば表面の単位長さ当たりの電流が求められます.
は普通の関数としては存在しませんが,δ関数を用いて表すことができるでしょう.
表面にだけしか電流が存在しなければ,電流密度がδ関数で表されるのは当然です.これをz=0を含む微小区間で積分すれば表面の単位長さ当たりの電流が求められます.
あるいは,表面をまたぐ長方形の閉曲線に積分形のアンペールの法則を適用することによって表面電流を求めることもできるでしょう.
>Fは常に同じ向きになるということは,どこかで振動項が打ち消しあって消えてしまうはずということでしょうか.
振動項が打ち消し合うのとは違うように思います.
たとえば,電流も磁場も 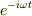 のように変化する場合,ローレンツ力は
のように変化する場合,ローレンツ力は 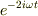 のように変化するわけではありません.
電流や磁場は実際は
のように変化するわけではありません.
電流や磁場は実際は 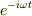 の実数部分の
の実数部分の 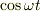 のように変化するので,ローレンツ力は
のように変化するので,ローレンツ力は 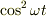 のように変化することになります.
のように変化することになります.
Re: 電磁波の運動量を求めるためのモデル
mNeji さんのレス (2008/07/02(Wed) 04:13)
>ですが,このモデルにそって解かなければならない問題なんです. >理論電磁気学は私もこの問題を調べるときに参照しました. >完全導体の反射は載っていたのですが,運動量のことまでは触れていなかったように思います.
う〜む,論点が逆でしたか,申し訳ありませんでした.「モデル部分」は自分で決めていいと感じました.
理論電磁気学の件は,高校生のころアマチュア無線に凝っていて高周波数の電流では「表皮効果」といって導体表面にしか電流が流れないことを知っていたのですが,正に「そのモデル」と思い感激したのです.
で,これなら運動量密度を求めれば分子運動論的に「光圧」の計算ができると踏んでいたので(計算せず),うろ覚えで書き込みました.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/02(Wed) 21:35)
>表面をまたぐ長方形の閉曲線に積分形のアンペールの法則を適用することによって表面電流を求めることもできるでしょう. デルタ関数が出てくるから,微分形のアンペールは使ってはいけないということですか?
それと,
実際の波は,波動関数と違って,実部のみが解になるわけですけど
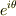 の二乗について考えたとき
二乗してから実部を取ると
の二乗について考えたとき
二乗してから実部を取ると
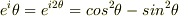 実部を取ってから二乗すると
実部を取ってから二乗すると
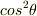 となって,違う答えが出てきます.(こっちのが正しいわけですよね?)
もともと計算を簡単にするために指数関数を導入したのだと思いますが
今までは,「全ての計算を終わったあと,最後に実部をとればいいや」くらいに思ってたのですけど,何かルールがあるのでしょうか.
となって,違う答えが出てきます.(こっちのが正しいわけですよね?)
もともと計算を簡単にするために指数関数を導入したのだと思いますが
今までは,「全ての計算を終わったあと,最後に実部をとればいいや」くらいに思ってたのですけど,何かルールがあるのでしょうか.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/03(Thu) 00:58)
微分形のアンペールの法則を用いれば,電流密度をδ関数を用いて表すことができるということです.それを積分すれば電流が求められます. 積分形のアンペールの法則を用いれば,直接電流を求めることができます.
物理量を複素数で表すのは計算の便宜上のことです.実際は実数で表される物理量に適当な虚数部分を付け加えて複素数にすることによって計算が簡単になるわけです. この場合,実数部分だけが実際の物理量であることを認識して計算する必要があります. 従って,和や差をとるときは複素数のまま計算して,あとから実部をとればよいのですが,積や商の計算では先に実部をとっておかないといけません. また,インピーダンスのように,実部と虚部がそれぞれ別々の物理量を表している場合は違う取り扱いが必要です.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/03(Thu) 16:54)
>積分形のアンペールの法則を用いれば,直接電流を求めることができます. 理解しました.境界条件を導くときと同じにやればいいんですね.
>積や商の計算では先に実部をとっておかないといけません. いままで意識せずに計算していました. 波動関数と違って,実部を取らなければならないなら,最初から三角関数で計算したほうが多少めんどうでも間違いをせずに済むかも・・・.
表面電流を求めるために,境界を挟む,長方形を考えます.y軸方向の長さlでz軸方向の長さは  とします.アンペールの法則より
とします.アンペールの法則より
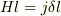 で,
で,  が無限に小さいとき,jは表面電流密度になるので,
が無限に小さいとき,jは表面電流密度になるので, 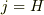 です.
よって,単位長さあたりの力は
です.
よって,単位長さあたりの力は 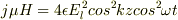 になって,一周期平均は
になって,一周期平均は
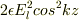 になりました.
になりました.
運動量の大きさは変わらないとすると,
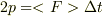 単位体積あたりの運動量は
単位体積あたりの運動量は
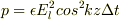 になりました.
Fを圧力ではなく,力だとすると
になりました.
Fを圧力ではなく,力だとすると
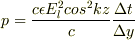 となります.
となります.
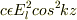 は入射波のポインティングベクトルになっていると思います.単位体積あたりの運動量は,ポインティングベクトルを光速の二乗で割ったものだったと思うのですが,もし,私の計算した式の最後の部分が光速になれば一致するのですけど,
は入射波のポインティングベクトルになっていると思います.単位体積あたりの運動量は,ポインティングベクトルを光速の二乗で割ったものだったと思うのですが,もし,私の計算した式の最後の部分が光速になれば一致するのですけど,  はどのように処理すればよいのでしょうか?
電磁波が衝突した時間に進む距離だから,
はどのように処理すればよいのでしょうか?
電磁波が衝突した時間に進む距離だから, 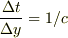 でしょうか.
でしょうか.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/04(Fri) 01:12)
電流が存在するのは導体表面だけなので,z=0 としないといけません. また,電流にはたらく力がその式でよいかどうかよく考えてみてください.
z軸方向に進む電磁波の単位体積 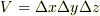 (
( 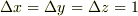 )の運動量を
)の運動量を 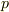 とし,これが単位面積
とし,これが単位面積 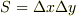 (
( 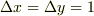 )に及ぼす平均の力すなわち圧力を
)に及ぼす平均の力すなわち圧力を 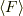 とすると
とすると
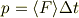
(これは間違っています.下記No.20680で訂正)
が成り立ちますが,ここで  は電磁波が
は電磁波が 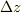 だけ進む時間です.
従って,
だけ進む時間です.
従って, 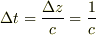 となります.
となります.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/05(Sat) 13:05)
電流に働く力がまちがっていますか?
電流に働くローレンツ力の式 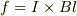 を今の問題に適用すると
圧力は
を今の問題に適用すると
圧力は 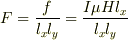 いま,表面電流密度は
いま,表面電流密度は 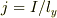 だから
圧力は
だから
圧力は 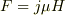 でしょうか?
でしょうか?
z=0では, 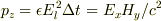 です.
です.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/05(Sat) 14:21)
すみません.
上に書いた 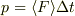 は間違いです.
運動量の変化が力積に等しいわけですから,正しくは
は間違いです.
運動量の変化が力積に等しいわけですから,正しくは
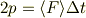
です.
圧力は 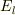 を用いて表してみてください.
を用いて表してみてください.
Re: 電磁波の運動量を求めるためのモデル
mNeji さんのレス (2008/07/05(Sat) 16:23)
やや不思議な気がするので,コメントさせて下さい.
難しい内部モデルは置いておくとしても,電磁波が導体に及ぼす圧力は,ある微小面積について,Δt間に流入する電磁波(入射波)のもつ運動量ベクタの総和と,流出する電磁波(反射波)のそれとの和で与える方が自然な感じがします.
如何なもでしょうか.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/05(Sat) 18:31)
確かにそのほうが簡単でしょうね.
それに対して,本問の意図は具体的なモデルによって圧力が生じる仕組みを考えさせることだと思います.
Re: 電磁波の運動量を求めるためのモデル
mNeji さんのレス (2008/07/05(Sat) 22:03)
>それに対して,本問の意図は具体的なモデルによって圧力が生じる仕組みを考えさせることだと思います.
これは十分に予想していました.でも,検算として常識的な計算を適応することも大切と思っています.特にファクタ2の出所は,本問の流れから間違え易いだろうと感じました.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/05(Sat) 22:16)
もちろん別の考え方で解いてみて比較してみることは有用でしょうね.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/06(Sun) 18:34)
圧力は 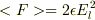 になりました.
運動量変化=力積をつかうと,No.20679のようになります.
になりました.
運動量変化=力積をつかうと,No.20679のようになります.
>yamaさん ひとつ疑問に思ったのですが,この問題の場合,磁場が完全導体内に電流を作るということになっていますが,普通は電場が導体内に電流を発生させるのではないのでしょうか?
>mNejiさん これは院試験の問題なので,わざとややこしくしているところもあるのだと思います. 私の持っている問題集では,入射波のエネルギー密度を微分して,導体に働く力を求め,そこから運動量を求めていました.
Re: 電磁波の運動量を求めるためのモデル
mNeji さんのレス (2008/07/06(Sun) 20:32)
>これは院試験の問題なので,わざとややこしくしているところもあるのだと思います.
なるほど,そういう事ですか.出題側も色々と工夫を凝らしている訳でしょうね.
>私の持っている問題集では,入射波のエネルギー密度を微分して,導体に働く力を求め,そこから運動量を求めていました.
はあ,回答としても各種の方法が有る訳ですね.色々な方法を知っているのは良い事だとおもいます.ただ,dP=Fdt はニュートンさんの昔からある上に,力学・流体力学・電磁気学と各種の場面に出て来るので,問題処理ツールとしては優れている様に思います.
>磁場が完全導体内に電流を作るということになっていますが
これについては,「完全導体内」としているので,抵抗密度σ=0となり,電場に依る電流を作れない,もしくは電場が内部に侵入できない,といったモデルなのかと感じていました.
【追記,2008-07-07, 11:00】
#抵抗密度σ=0のところは,以前書いたオームの法則, 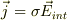 と普通のオームの法則,V=RIがごちゃ混ぜになっている様です.
#でも,ある種の専門領域では,このようなモデル化が行われているのかも知れませんね.どうも失礼いたしました.
と普通のオームの法則,V=RIがごちゃ混ぜになっている様です.
#でも,ある種の専門領域では,このようなモデル化が行われているのかも知れませんね.どうも失礼いたしました.
もし,自分が回答者ならば「それを批判する意見」を書いてしまいそうです....
#教育的観点から,このような発言はいけないことと思います. #たまには,異論が在っても善いかも知れませんので,撤回はしません.
なお,試験対策という事で思い出したのですが,二電子系のスピン・スピン相互作用の時の話ですが,言いそびれたのでコメントしておきます. 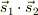 は内積でそれぞれのベクタの絶対値の積と,それぞれのベクタの成す角度の余弦です.この為に,量子力学でも,座標の取り方に左右されない値となります.一般に角運動量の量子化は,ちょっと直感から外れますが,この内積がたの相互作用だけは「筋がいい」ですね.
は内積でそれぞれのベクタの絶対値の積と,それぞれのベクタの成す角度の余弦です.この為に,量子力学でも,座標の取り方に左右されない値となります.一般に角運動量の量子化は,ちょっと直感から外れますが,この内積がたの相互作用だけは「筋がいい」ですね.
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/06(Sun) 23:32)
ポインティングベクトルを利用して平均の圧力を求めてみましょう. z=0 における入射波のポインティングベクトルの大きさは
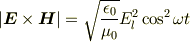
となるので,1周期の平均は
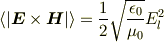
となります.
平均の運動量密度 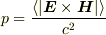 と平均の圧力
と平均の圧力 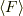 の間には
の間には 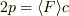 の関係があることから
の関係があることから 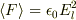 が得られます.
しかし,これはメントスさんが求めた圧力と一致しません.どうしてでしょうか? 考えてみてください.
が得られます.
しかし,これはメントスさんが求めた圧力と一致しません.どうしてでしょうか? 考えてみてください.
>ひとつ疑問に思ったのですが,この問題の場合,磁場が完全導体内に電流を作るということになっていますが,普通は電場が導体内に電流を発生させるのではないのでしょうか?
その通りですが,完全導体の場合は,内部の電場は0であり,本問の場合は表面の電場も0になります.電気伝導率 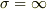 なので電流密度は
なので電流密度は 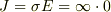 となり,電流密度が定まりません.
となり,電流密度が定まりません.
従って,磁場についての条件から電流を定める必要があります.
Re: 電磁波の運動量を求めるためのモデル
スチーム さんのレス (2008/07/08(Tue) 09:53)
メントスさん. yamaさんが指摘されているように解法に間違いがあります.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/10(Thu) 13:03)
返信おそくなり申し訳ありません.
2倍だけ違うということは,直感的に考えて,電流に働く力の要因である磁場を
定常波の磁場としたことが原因でしょうか.
入射波だけの磁場が電流に作用すると考えると
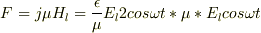 となり
一周期の平均は
となり
一周期の平均は
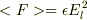 になると思います.
しかし,なぜそうなるのかが分からないです.
磁場の定常波(入射波と反射波)によって表面に電流が出来て,入射波だけが電流と作用するということですよねぇ・・・.
になると思います.
しかし,なぜそうなるのかが分からないです.
磁場の定常波(入射波と反射波)によって表面に電流が出来て,入射波だけが電流と作用するということですよねぇ・・・.
伝導率が無限だから,電場からは電流は求まらないとのことですが, それは数学的にということですか?それとも,実際に起きている現象でもそうなのでしょうか? 完全導体は導体の特殊な例だと思いますが,導体のときは電場によって電流が作られて,完全導体のときは磁場によって電流が作られるというのが少し納得できないです(現象的には同じことなのでしょうか?電場と磁場は本質的には同じものと聞いたことがありますが・・・)
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/10(Thu) 23:20)
定常波ができるのはz<0の部分です.z>0では磁場は0です.
では電流が存在するz=0の磁場は?
大雑把に考えて,両側の磁場の平均と見なすと 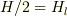 となり,これを用いて計算した平均圧力はポインティングベクトルから求めたものと一致します.
しかし,z=0の磁場が両側の磁場の平均になるかどうかは疑問が残りそうです.
となり,これを用いて計算した平均圧力はポインティングベクトルから求めたものと一致します.
しかし,z=0の磁場が両側の磁場の平均になるかどうかは疑問が残りそうです.
次のように考えることもできます. 観察される磁場は,入射波の磁場と,電流による磁場の重ね合わせです. 電流による磁場がその電流自身に及ぼす力は,全体としては0になると考えられます.そうすると電流にはたらく力としては,入射波の磁場が電流に及ぼす力だけを考えればよいことになるわけです.
同じような例として,コンデンサの極板間の電場がEで,極板の電荷がQであるとき,極板にはたらく力が QE/2 になることも同様に考えることができますね.
>完全導体は導体の特殊な例だと思いますが,導体のときは電場によって電流が作られて,完全導体のときは磁場によって電流が作られるというのが少し納得できないです
磁場によって電流がつくられるのではなく,電流が磁場をつくるわけです.その磁場が満たすべき条件から電流が定まるということです. 完全導体でない導体を考えて,その電気伝導率を限りなく大きくした極限が完全導体であると考えることができます. 完全導体でない場合,電磁場は導体内部にも侵入します.侵入した電場は電流を生じますが,同時にその電流が磁場を生じます. これらの電場,磁場,電流は相互に関連し合っていますが,マクスウェル方程式を用いて定めることができます. その結果,電磁場や電流は表面から内部に向かって急速に減衰し,いわゆるスキンデプスのあたりまでしか存在しないことになります. 電気伝導率を大きくすると,スキンデプスは減少し,極限では0になります.つまり電流は表面電流だけになり,電流密度は無限大になりますが,電流は有限になり,その電流のつくる磁場によって内部の磁場が打ち消されることになります. 従って,完全導体の内部の磁場が0になるという条件から表面電流を求めても同じことになるわけです.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/12(Sat) 21:53)
ありがとうございます. >観察される磁場は,入射波の磁場と,電流による磁場の重ね合わせです. 反射波の磁場は観測されないのですか? 電流による磁場が反射波のことですか?(つまり,反射されるメカニズムは,磁場が入射→電流発生→電流が作った磁場が入射波と反対方向に放射されるということでしょうか)
>つまり電流は表面電流だけになり, 詳しいメカニズムは,完全導体単独で考えることは不可能で 導体の極限によって与えられるということでしょうか. 現実に,完全導体って存在するんですよね?
Re: 電磁波の運動量を求めるためのモデル
yama さんのレス (2008/07/13(Sun) 00:08)
電流による磁場が反射波の磁場です. 表面電流による磁場とそれにともなう電場は,電磁波として内部と外部に向かって放射されます. 内部に向かって放射される電磁波は入射波を打ち消し,外部に向かって放射される電磁波(反射波)は入射波と重なって定常波をつくります. その定常波が観察されるわけです.
完全導体は,電気伝導度を限りなく大きくした極限の導体であると考えることができます. 従って,完全導体中の電流密度は
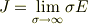
となります.これが 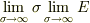 に等しくないことは数学的に明らかだと思います.
なお,完全導体が存在するかどうかは分かっていません.
超伝導体を完全導体と見なすこともありますが,表面付近は超伝導状態にならず,電磁場が侵入できるので,電磁波の反射を考える場合は完全導体とは言えないでしょう.
に等しくないことは数学的に明らかだと思います.
なお,完全導体が存在するかどうかは分かっていません.
超伝導体を完全導体と見なすこともありますが,表面付近は超伝導状態にならず,電磁場が侵入できるので,電磁波の反射を考える場合は完全導体とは言えないでしょう.
Re: 電磁波の運動量を求めるためのモデル
メントス さんのレス (2008/07/13(Sun) 00:11)
なるほど.電磁波の反射のメカニズムがよく理解できました. ありがとうございました.
>なお,完全導体が存在するかどうかは分かっていません. そうなのですか.導体を基本に考えれば良いのですね.