惑星 極座標 運動方程式
惑星 極座標 運動方程式
たけ さんの書込 (2008/06/30(Mon) 15:18)
今大学1年です.
惑星の極座標の方程式に関する質問です.
極座標の原点を楕円 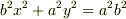 の中心(x=0,y=0)にとります.
の中心(x=0,y=0)にとります.
![m[\frac{d^2r}{dt^2} -r(\frac{d\Theta}{dt} )^2 ]=Fr](http://hooktail.maxwell.jp/bbslog/49cbe66137957c9749423d27a0f58e1e.png)
面積速度一定
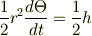
を利用して,
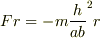 を証明せよという問題です.
いまのところ,
を証明せよという問題です.
いまのところ, ![r=\frac{b}{\sqrt[]{\mathstrut 1+ecos^2\Theta} } (e=\frac{b^2-a^2}{a^2} )](http://hooktail.maxwell.jp/bbslog/8939b2a865144748a4c146143bf5e3fc.png) とおいて
とおいて
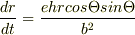 となったのですが
となったのですが
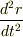 がぐちゃぐちゃになってしまい,3時間近く考えているのですが,どうしようもなく,ここに相談しました.
がぐちゃぐちゃになってしまい,3時間近く考えているのですが,どうしようもなく,ここに相談しました.
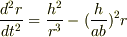 とすることができれば解けるのですが・・・
大変恐縮なのですが,このあとどうすれば解けるのでしょうか?教えてください.
とすることができれば解けるのですが・・・
大変恐縮なのですが,このあとどうすれば解けるのでしょうか?教えてください.
Re: 惑星 極座標 運動方程式
yama さんのレス (2008/06/30(Mon) 15:48)
たけさんが書かれている運動方程式と面積速度一定の式は太陽を原点にとったときの式です. ところが,太陽は楕円の1つの焦点にあるのであって,楕円の中心にあるわけではありません. 従って,楕円の中心を原点にとった場合の運動方程式はたけさんが書かれた形にはなりません.
Re: 惑星 極座標 運動方程式
たけ さんのレス (2008/06/30(Mon) 15:58)
>>yamaさん 返答ありがとうございます. 私の式は楕円中心のものだと思うのですが・・・ 太陽を中心の場合,分母に根号が入らない形ではないでしょうか?
Re: 惑星 極座標 運動方程式
yama さんのレス (2008/06/30(Mon) 16:12)
rを表す式は楕円中心を原点としたものですね. ところが運動方程式と面積速度一定の式は太陽を原点としたものです. つまり,原点のとりかたの異なる式が混在しているということです.
と書きましたが,運動方程式については,楕円中心を原点にとっても同じ形にはなりますね.ただし,その場合は 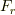 がrだけの関数ではなくなります.
がrだけの関数ではなくなります.
Re: 惑星 極座標 運動方程式
スチーム さんのレス (2008/06/30(Mon) 17:03)
横から失礼します. たけさんの方法はまっとうですが,やや困難です. そこで極座標系からx−y座標系で考え直すと容易です. 二次元の振動の問題ですので.
Re: 惑星 極座標 運動方程式
yama さんのレス (2008/06/30(Mon) 17:10)
証明すべき式をよく見ると,力はrに比例する引力のようですね.
惑星の運動の場合は,力は 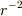 に比例するはずなので,惑星の運動ではないように思います.
rに比例する引力がはたらくということは,2次元の調和振動だと思います.
そうだとすれば,楕円の中心を原点にとったとき,運動方程式と面積速度一定の式はたけさんが書かれた式になりますね.
に比例するはずなので,惑星の運動ではないように思います.
rに比例する引力がはたらくということは,2次元の調和振動だと思います.
そうだとすれば,楕円の中心を原点にとったとき,運動方程式と面積速度一定の式はたけさんが書かれた式になりますね.
ところで,問題文には惑星の運動と書いてあるのでしょうか?
Re: 惑星 極座標 運動方程式
たけ さんのレス (2008/06/30(Mon) 17:49)
>>スチームさん ありがとうございます. 試してみます. >>yamaさん 惑星とは書いてませんでした... 本当にすみません.誤解を生じさせてしまいました.
Re: 惑星 極座標 運動方程式
たけ さんのレス (2008/07/01(Tue) 00:39)
やはりできませんでした・・・
Re: 惑星 極座標 運動方程式
スチーム さんのレス (2008/07/01(Tue) 09:08)
ヒント x=acosφ y=bsinφ とおき, 面積速度一定より, 速度を(u,v)とすれば xv-yu=h (u=dx/dt,v=dy/dt) 以上から,dφ/dtを決定.
Re: 惑星 極座標 運動方程式
komagatake さんのレス (2008/07/01(Tue) 17:51)
私もやってみました. かなり時間がかかりました. 3時間以上です.
計算の方針が決まっていても確かにそうなるということを確めるだけでもかなりの時間がかかります.3時間でできるという保障はないのですから投げずにがんばってください.
面積速度一定は中心力の場合はいつも成り立ちます. 軌道の形が決まれば力の表現が決まるはずです.
極座標でやってみます. r^2[(cosφ)^2/a^2+(sinφ)^2/b^2)]=1 この式を時間で微分するとdr/dt,dφ/dtの関係式が出ます. hを使って書き直すと dr/dt=hr(cosφ)(sinφ)(1/a^2−1/b^2) になります.これをまた時間で微分して整理して d^2r/dt^2−r(dφ/dt)^2 を計算すると−h^2r/a^2b^2が出てきます. (a,bに2乗がつくはずです.)
計算の最後で (a^2−b^2)[a^2(sinφ)^4−b^2(cosφ)^4] が出てきますが簡単になりますから投げずにやってください.
ご質問の最初にある離心率を使った楕円の表現は焦点のひとつを原点としたものですから正直にやれば1/r^2の形の引力が出るはずです.
6/3016:31のレスにある式 d^2r/dt^2=h^2/r^3−ah^2/b^2r^2 をFrの式に代入すると万有引力の式が出てきます. (1項目が消えて2項目だけが残ります.)
Re: 惑星 極座標 運動方程式
たけ さんのレス (2008/07/02(Wed) 01:32)
みなさんありがとうございました. 昨日は一睡もできず,結局解けずじまいだったのですが, komagatakeさんのやり方ですらすらといきました. 本当にありがとうございます.
Re: 惑星 極座標 運動方程式
komagatake さんのレス (2008/07/02(Wed) 08:08)
たけさん
komagatakeです. できたようですね.
これで万有引力の場合と調和振動の場合と2つできた事になります. どちらも楕円ですがrの中心の位置が異なります.
Re: 惑星 極座標 運動方程式
komagatake さんのレス (2008/07/02(Wed) 11:34)
komagatakeです.
r^2(1+e(cosφ)^2)=b^2 dr/dt=ehrcosφ・sinφ/b^2
でも出来るはずだと思ってやってみました.
最期の結果をeとcosφで書くとrに変換出来ますので d^2r/dt^2=(1/r^3−r/(ab)^2)h^2 が出てきます. でも最期の結果がなかなか簡単な形になりませんでした. 一度rをくくりだして rh^2[]の形にしてからやるとうまく変換できて簡単な形になりました.
初めにやりかけた方法で正しかったのです. どこで行き詰ったかを確めておくといいと思います.
これで私の方もすっきりしました.
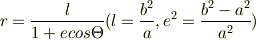
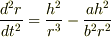 となってしまい,だめでした.
となってしまい,だめでした.