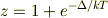space さんの書込 (2008/06/30(Mon) 06:06)

はじめまして．spaceといいます．今，大学院１回生です． Schottoky比熱について聞きたいんですが，課題で以下のような問題が出ました．

上下準位間のエネルギー間隔が?である二準位系を考える．比熱C=∂<E>/∂Tの関係から，Schottoky 比熱C=(?^2/kT^2)*(exp(?/kT)/(1+exp(?/kT))^2を導出せよ．また，T>>?のとき，比熱がT^(-2)に比例することを示せ．

という内容です．比熱C=∂<E>/∂Tの関係とありますが，Cがどのような式なのかがわかりません．「T>>?のとき，比熱がT^(-2)に比例することを示せ．」に関しては，exp(?/kT)→0という感じで解くんだとおもうんですが…． わかる方ぜひお願いします．

yama さんのレス (2008/06/30(Mon) 11:40)

次の手順で解けると思います． １．まず分配関数を求める． ２．それを用いてエネルギー<E>を温度の関数として求める． ３．比熱C=∂<E>/∂Tを計算する．

>比熱C=∂<E>/∂Tの関係とありますが，Cがどのような式なのかがわかりません．

この関係は比熱の定義式であって，Cがどのような式なのか初めから分かっているわけではありません． この式にあてはめて計算すればSchottoky 比熱Cの式になるということです．

なんとなく さんのレス (2008/06/30(Mon) 11:55)

yamaさんが触れられなかったので，一言．

>「T>>?のとき，比熱がT^(-2)に比例することを示せ．」に関しては，exp(?/kT)→0という感じで解くんだとおもうんですが…．

T>>?つまり，Δ/T<<1のとき，exp(?/kT)→0ではなく， exp(?/kT)→1+?/kT+(?/kT)^2/2!・・・ですよ．

space さんのレス (2008/06/30(Mon) 12:36)

回答ありがとうございます． 分配関数を求めるということだったんですが，E=?e^(-?/kT)/Σe^(-?/kT) ということでいいんでしょうか？ 分母を計算すると，?e^(-?/kT)(1-?e^(-?/kT))^(-1)という風になると思うんですが，ここからEを求めてTで微分しても，導出する式と合いません． 間違っているところのご指摘お願いします．

space さんのレス (2008/06/30(Mon) 12:40)

そうですね…，exp(?/kT)→1でした．すいません…．

yama さんのレス (2008/06/30(Mon) 15:28)

低い方のエネルギー準位を とすると，分配関数は次のようになります．

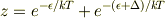
比熱はエネルギーの基準のとりかたに関係しないので，簡単のため 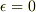とすると分配関数は次のようになります．

space さんのレス (2008/06/30(Mon) 16:42)

ありがとうございます！解けました！ 分配関数から，期待値<E>を求めてTで微分したらいけました．