Kuroneko さんの書込 (2008/06/29(Sun) 21:11)

大学１年生です． 「半径aの内筒，内半径bの外筒が，中心に一致するように置かれており，内筒には密度σで電化が一様に分布している．このとき，内外筒間のならびに外筒のポテンシャルをゼロとした場合の，内筒のポテンシャルを求めよ．」 という問題なのですが，積分するときどのような範囲で積分をすればいいのかよく分からなく困っております．どうか，よろしくお願いします．

toorisugari no Hiro さんのレス (2008/06/30(Mon) 13:52)

半径 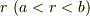における電場(電束密度)ベクトルを求めてください．

Kuroneko さんのレス (2008/07/03(Thu) 22:18)

ガウスの法則より， E=aσ/εr 通常なら，無限遠を基準点とし積分を行うのですが，この場合はbを基準点として，bからaまで積分を行うのでしょうか？

toorisugari no Hiro さんのレス (2008/07/03(Thu) 23:20)

> ガウスの法則より， > E=aσ/εr

「内筒には密度σで電化が一様に分布している」がよくわかりませんが， 「内筒表面に面密度σで電荷が一様に分布している」ということなら，あっています．

> この場合はbを基準点として，bからaまで積分を行うのでしょうか？

問題文の

>> このとき，内外筒間のならびに外筒のポテンシャルをゼロとした場合の，内筒のポテンシャルを求めよ．

が日本語として意味不明ですが，「外筒の電位を0としたときに，内筒の電位を求めよ」ということなら，おっしゃるとおりです．

Kuroneko さんのレス (2008/07/04(Fri) 20:36)

すっきりしました．どうも，ありがとうございました．

Kuroneko さんのレス (2008/07/13(Sun) 19:48)

すいません，上の問題で，内外筒間の電場をぜロとし外筒のポテンシャルもゼロとする場合も同じようにすればいいのでしょうか？お願いします．