マクスウェル方程式の移流方程式
マクスウェル方程式の移流方程式
Smith さんの書込 (2008/06/29(Sun) 17:30)
初めまして,こんにちは. 数値シミュレーションに興味をもっている大学4年です.
電磁波シミュレーションでは, 中央差分法と蛙飛び法を用いたFDTD法が広く普及していますが, より高精度と称されるCIP法では,エルミート補間と移流方程式を用いています.
CIP法の利点の1つは,FDTD法のような物理的でない「吸収境界条件」を 設定せずに済み,計算時間とメモリが節約されることです.
しかしCIP法も電磁波の波形をエルミート補間していたり, 移流方程式を各方向に分離して解いたりと, およそ物理的ではないように私は感じます. (限られた時間とコストで計算するために近似は避けられませんが…)
ただ,マクスウェル方程式を直接解くのではなく, その移流方程式を解いている点は注目に値すると思います. (浅学のため,見当違いかもしれませんが…)
そこで,どのような非弾性現象でも保存される物理量である エネルギーと電荷量の移流方程式を利用して 電磁波解析を行おうと考えています.
線形かつ等方性である媒質では マクスウェル方程式から以下のエネルギー保存則が導かれます.
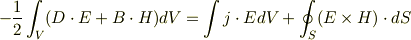
右辺の第1項はジュール熱による単位時間当たりのエネルギー損失で,
第2項は境界面  から流出するエネルギーの流れです.
から流出するエネルギーの流れです.
上の式は移流方程式となっているのでしょうか?
www.fml.m.dendai.ac.jp/iwatsu/docs/cfd-lec-07-02.pdf
によると,保存される物理量がベクトル  である場合,
フラックスはテンソル
である場合,
フラックスはテンソル  ,体積ソースはベクトル
,体積ソースはベクトル 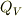 ,
表面ソースはテンソル
,
表面ソースはテンソル 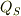 とすると移流方程式は
とすると移流方程式は
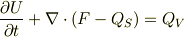
となるそうです.
電子が加速度運動する際に電磁波を放射するような
(シンクロトロン放射,チェレンコフ放射,制動放射)系を考えると,
1番目の式では電子がもつ運動エネルギーが含まれてないですし,
2番目の式の体積ソース 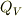 や表面ソース
や表面ソース 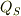 を
どのように考えたらよいのか…
を
どのように考えたらよいのか…
かなり長い文なりましたが, 読んで下さった皆様,ありがとうございます. お忙しいとは存じますが,よろしくお願いいたします.
Re: マクスウェル方程式の移流方程式
mNeji さんのレス (2008/06/29(Sun) 20:05)
Smithさん,初めまして.
私は,流体力学の応用に興味が有る者ですが,なかなか具体的な解析ができないでいます.
逆にお聴きしたいのは,流体力学では「速度場」を対象とする為に「移流項」が出て来ると思っていたのですが,電磁場の「移流項」とはどのような解釈をされているのでしょうか?それとも電磁流体力学的な場合でしょうかね.
Re: マクスウェル方程式の移流方程式
Smith さんのレス (2008/06/30(Mon) 18:56)
こんばんは.
物理学辞典(培風館)によりますと 濃度や熱などの物理量が,それを担う流体の運動によって運ばれる過程 が「移流」とされています.
しかし,電磁気学において電磁流体を考えなくとも CGSガウス単位系でのマクスウェル方程式を 成分ごとに解く際に変形を工夫すると 移流方程式の形になります. 詳細はCIP法を発明した矢部さんの著書に書かれています.
単位系を変えても本質は同じはずですから 移流方程式とは何かと調べると,保存則を意味していることが 分かった次第であります.
しかし言葉の意味のみで内容を理解していないため 上のようにご質問致しました.
Re: マクスウェル方程式の移流方程式
mNeji さんのレス (2008/06/30(Mon) 20:03)
>物理学辞典(培風館)によりますと >濃度や熱などの物理量が,それを担う流体の運動によって運ばれる過程 >が「移流」とされています.
この意味ならば,私も理解出来そうです.
>しかし,電磁気学において電磁流体を考えなくとも >CGSガウス単位系でのマクスウェル方程式を >成分ごとに解く際に変形を工夫すると >移流方程式の形になります. >詳細はCIP法を発明した矢部さんの著書に書かれています.
これは全く存知ません.その本に従って勉強されるのが一番だろうと思います.
>単位系を変えても本質は同じはずですから >移流方程式とは何かと調べると,保存則を意味していることが >分かった次第であります.
ちなみに,流体力学での速度場 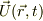 では,場の量の時間微分がラグランジェの微分となり話が込み入ります.その一例として,加速度場,
では,場の量の時間微分がラグランジェの微分となり話が込み入ります.その一例として,加速度場, 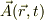 を考えると,自分自身の変化に自分が出て来るという面倒な事になる訳です;
を考えると,自分自身の変化に自分が出て来るという面倒な事になる訳です;
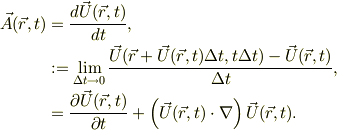
この最後の部分が速度場での「移流項」を表し,速度場について2次の非線形となっているので,問題が難しいくなる元凶だとおもいます.
でも,ベクタ解析のお陰で,
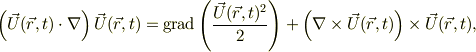
と変形出来るのが有難いことだと思います.
右辺第1項は運動エネルギー密度の勾配,すなわち運動エネルギの移流に対応し,第2項は局所的な回転(渦)に対応すると思います.
# この第1項は運動方程式を全て書き下して行けば,定常的な場の流体場ではベルヌーイの定理に至るとおもいます.
しかしながら,私見ですが,移流項は本質的に非線形なので,純粋に電磁気の領域には持ち込まない方が良い様に感じています.
#ヒョットして,電磁エネルギ密度,電磁運動量密度などから出発して,解析力学的に定式化でもされているのかも知れませんね. #数値計算手法では,線形性よりも,数値計算の収束性や,計算アルゴリズムの単純性のほうが優先するとか....
CIP法を勉強されて電磁気への応用が判ったら,是非とも教えて戴きたいものです.
Re: マクスウェル方程式の移流方程式
toorisugari no Hiro さんのレス (2008/06/30(Mon) 20:28)
> 移流方程式とは何かと調べると,保存則を意味していることが分かった次第であります.
誤解されているようですが,移流方程式と保存則は別物です.
電荷の保存則(空間一次元にしています)
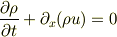
を変形すると移流方程式
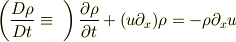
になりますが,逆は一般に成り立ちませんし,数値計算では別物です.
第1式は有限体積法(1次元では中央差分法+蛙飛び法)
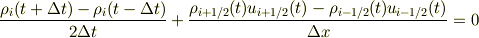
で解かれることが多いですが,( 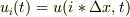 としています.)
第2式は有限差分法(風上差分)
としています.)
第2式は有限差分法(風上差分)
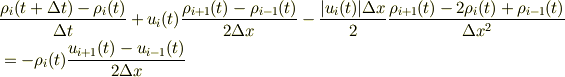
あるいはCIP法
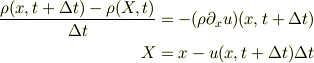
で解かれることが多く,これらは違うものです.
Re: マクスウェル方程式の移流方程式
Smith さんのレス (2008/06/30(Mon) 20:51)
mNeji さん
返信ありがとうございます. この本に書かれているCIP法をよく理解してみます.
toorisugari no Hiro さん
返信ありがとうございます. 保存則と移流方程式は別の手法を用いて数値計算されるということですか? 例示された保存則の偏微分を展開した式が移流方程式になっているという解釈も 誤りなのでしょうか?
Re: マクスウェル方程式の移流方程式
toorisugari no Hiro さんのレス (2008/06/30(Mon) 20:54)
> 例示された保存則の偏微分を展開した式が移流方程式になっているという解釈も誤りなのでしょうか?
OKですが,せっかくの保存性がきえてしまいます.
Re: マクスウェル方程式の移流方程式
toorisugari no Hiro さんのレス (2008/06/30(Mon) 21:11)
> 顕著に数値拡散が生じるのでしょうか? というより 「保存則」という基本的性質が成り立ちません. 数値拡散や打ち切り誤差があっても積分量が一定ならOKですが,移流方程式(を基にした数値計算法)ではlocalな積分形の保存則は保証されません.
Re: マクスウェル方程式の移流方程式
Smith さんのレス (2008/06/30(Mon) 21:19)
toorisugari no Hiro さん
何度も質問してしまい申し訳ございません. 数値計算は奥が深いと聞きましたが, まさに目から鱗です. 勉強しなおして参ります. ありがとうございました.