制御ゲインの求め方
制御ゲインの求め方
ゆう さんの書込 (2008/06/29(Sun) 00:46)
大学3年生のゆうといいます. 倒立振り子の制御問題で制御ゲインを決める方法を教えてください. 以下のページに丁度よいサンプルがありました. ttp://www.isas.ac.jp/sokendai/examination/pdf/01_physics.pdf
運動方程式はMaximaというソフトを使い,ラグラジアンを導き,運動方程式まで立てることができました. 上記プリントとプログラム上の違う所は M→m1 m→m2 x方向をz θ→q としています.
----プログラム------------------------------------------------------ depends([z, q],[t]); declare(g, constant,l,constant,m1,constant,m2,constant,I,constant);
z1: matrix([z],[0]); z2: matrix([z+l*sin(q)],[l*cos(q)]);
v1: diff(z1,t); v2: diff(z2,t);
T1: m1 / 2 * v1.v1; T2: m2 / 2 * v2.v2 + I / 2 * diff(q,t)^2; T: T1+T2;
U1: 0; U2: m2 * g * l * cos(q); U: U1 + U2;
L: T - U;
Lz: expand(diff(diff(L,diff(z,t)),t) - diff(L,z)); Lq: expand(diff(diff(L,diff(q,t)),t) - diff(L,q));
M: matrix([coeff(Lz, diff(z,t,2)), coeff(Lz, diff(q,t,2))] , [coeff(Lq, diff(z,t,2)), coeff(Lq, diff(q,t,2))]); G: matrix([coeff(Lz, g)], [coeff(Lq, g)])*g; h: expand(matrix([Lz],[Lq]) - M.matrix([diff(z,t,2)],[diff(q,t,2)]) - G); ----プログラムここまで------------------------------------------------------
運動方程式は 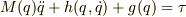 となり
Mが慣性行列,hが遠心力,コリオリ力,Gが重力項は以下のようになりました.
となり
Mが慣性行列,hが遠心力,コリオリ力,Gが重力項は以下のようになりました.
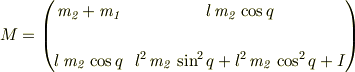
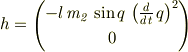
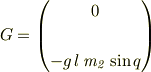
ここで 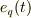 を,現在の角度
を,現在の角度 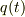 と目標の角度
と目標の角度 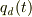 の差とした場合に
台車へ力
の差とした場合に
台車へ力  を加え
を加え 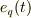 を0にするよう制御する場合,このようにすればよいらしいのですが
を0にするよう制御する場合,このようにすればよいらしいのですが
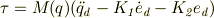
どのように 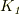 ,
, 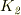 を求めれば良いのでしょうか?
を求めれば良いのでしょうか?
Re: 制御ゲインの求め方
mNeji さんのレス (2008/06/29(Sun) 14:27)
一種の連成系の問題で,難しそうですね.でも,小学生の頃,30cmくらいの定規を掌の上立てて,動的な安定を作ろうとしたのと似ていますね.
ご紹介のJAXAのサイトの図では,棒の部分の慣性能率が無視してありますが,結構聴きそうな気もします.何れにしろ,棒の長さを長めにとれば安定方向に向かいますね.
さて,外力fをどのようにして制御系に入れるのかを知らないので「倒立振り子 制御問題 制御ゲイン」で検索をすると,
という資料がありましたが参考になりませんか?
Re: 制御ゲインの求め方
ゆう さんのレス (2008/06/29(Sun) 23:11)
こんばんは.
> 小学生の頃,30cmくらいの定規を掌の上立てて,動的な安定を作ろうとしたのと似ていますね.
そうですね,まさにこれのことです.
教えていただいたURL参考になりそうです. もう少しみてみます.
実際にプログラムをし動かしてみたところ,(目標角度−現在の角度)*適当なゲインで動きます... こんなものなのかもしれません.
Re: 制御ゲインの求め方
mNeji さんのレス (2008/06/30(Mon) 01:45)
>実際にプログラムをし動かしてみたところ,(目標角度−現在の角度)*適当なゲインで動きます...
実際の演算過程を知らないので判りませんが,制御する場合,演算中値と計測した値には計測系に於ける遅延時間が存在します.また,外力を発生するには演算する為の有限時間幅と,外力を生成する駆動系の遅延時間もあると思われます.
勿論,系の力学的固有振動,ゲイン,制御系の遅延時間などがすべて絡むのでしょうね.