教えてください

教えてくださいさんの書込 (2008/06/27(Fri) 23:38)

厚さが無視できる半径0.2(m)の球殻に＋６×１０^−10(c)の電荷が一様に分布している．球の中心からr(m)の位置における電場の強さをもとめよ．

返信ありがとうございます．ほんとうにすみませんが，実際に数字をあてはめて答えをおしえていただきませんか？計算がわからないのです．本当にすみません．

半径 ,電荷とします．（電荷の値が文字化けしておられます）

ガウスの法則より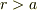， r>a では

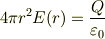
$4\pi r^2E(r)=\frac{Q}{\varepsilon_0}$

よって

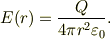
$E(r)=\frac{Q}{4\pi r^2\varepsilon_0}.$

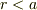r<a では，電荷が存在しないので， E(r)=0 .

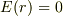ガウスの法則は

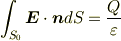
$\int_{S_0}\bm{E}\cdot\bm{n}dS=\frac{Q}{\varepsilon}$

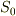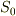左辺は閉曲面 S_0 上の面積分で，は S_0 内に含まれる全電荷です．

この場合，電場が球対称に分布すると考えられるので，これで簡単に解けたわけです．

＞ガウスの法則より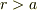， r>a では

とありますが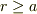， $r \ge a$ として置く方が表面での電荷密度と電場強度との関係を把握しやすいと思います．

と書いてしまいましたが，これが球殻が絶縁体の場合を想定していました．

もし金属でしたら入れない方が良いですね．