運動方程式の合力の向き
運動方程式の合力の向き
kuma(高2) さんの書込 (2008/06/22(Sun) 02:05)
はじめまして. 高校物理に関して質問があります.
【問】
水平面上に置かれた質量Mの箱Qの中に質量mの小物体Pを入れ,
静止状態から箱に外力Fを水平右向きに加えて運動させる.
PとQの間の静止摩擦係数を 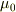 ,動摩擦係数を
,動摩擦係数を 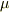 とし,
Qと水平面上の間の動摩擦係数も
とし,
Qと水平面上の間の動摩擦係数も 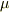 とする.
重力加速度を
とする.
重力加速度を 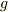 とする.
とする.
まず, 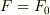 の時,P,Qは一体となって運動した.
の時,P,Qは一体となって運動した.
(2)PがQから受けている摩擦力の大きさfを求めよ.
(河合出版 浜島清利著 名問の森物理 力学・波動 p31より)
この問題の解答部分には
Pの加速度を右向き正とすると fも右向きになる
といったような事が書かれています.
運動方程式の加速度の向きと合力の向きは 一致するということは知っているのですが,
運動方程式には向きが逆の場合 例えば
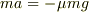
などといったもののの場合, 加速度の向きと合力の向きは 一致していないと思うのです. (だからマイナスの符号をつけて表現しているはず) しかしこの運動方程式も成立します.
今回の問題の場合も fが右向きなら当然運動方程式は成立し fが左向きでも マイナスをつければ運動方程式は成立するはずですから 加速度の向きだけで fの向きを判定できるというのは いまいち自分の中で納得がいきません.
加速度の向きだけで fの向きを判定できる根拠をどなたか 教えてもらえませんか??
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/22(Sun) 03:27)
kuma(高2)さん,初めまして.高校生さんなのに数式表現が使えるのは凄いですね.
水平台の一点,Oを原点とする静止座標系(右の方向を正とする)から,
箱Q(質量M)の加速度を  物体P(質量m)の加速度を
物体P(質量m)の加速度を 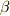
そうすると,力と運動方程式は, 〜〜〜〜現在:再検討中〜〜〜〜

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
考える要点として,
(1)QとPとには摩擦力による相互作用しか無いことと,
(2)Qに外力  を加えた時に,Pからの相互作用
を加えた時に,Pからの相互作用 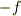 は減速方向しかあり得ないこと
だと思います.
は減速方向しかあり得ないこと
だと思います.
Re: 運動方程式の合力の向き
kuma(高2) さんのレス (2008/06/22(Sun) 05:15)
おはようございます! 御解答ありがとうございました.>mNejiさん
mNejiさんのレスについて 2つ疑問点があるのですがよろしいでしょうか?
まず1つ目は運動方程式についてで (重箱の隅をつつくようで申し訳ないのですが)
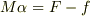
とされていますが
これは
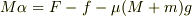
ではないでしょうか??
Qと床の間にも摩擦力が働いているので それも式に入れる必要があるように思います.
(僕の思い違いの可能性がありますが...)
2つ目は >(2)Qに外力Fを加えた時に,Pからの相互作用−fは減速方向しかあり得ない
についてで 自分はQがPのせいで動きづらくなっている(Pからの相互作用−fのため) と考えたのですがこの理解であっているんでしょうか?
暇を見てまた返信していただけると ありがたいです.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/22(Sun) 10:14)
>これは
>
> 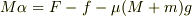 >
>ではないでしょうか??
>
>Qと床の間にも摩擦力が働いているので
>それも式に入れる必要があるように思います.
>
>ではないでしょうか??
>
>Qと床の間にも摩擦力が働いているので
>それも式に入れる必要があるように思います.
そうですよね,忘れていました.お説の通りです.また,自分の書いた式では, 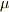 を動摩擦係数としないで,静止摩擦係数〜動摩擦係数を含んだ一般的な摩擦係数の積もりで書いていました.下手に直すと,混乱しそうなのでしばらく時間をください.;-P)
を動摩擦係数としないで,静止摩擦係数〜動摩擦係数を含んだ一般的な摩擦係数の積もりで書いていました.下手に直すと,混乱しそうなのでしばらく時間をください.;-P)
>自分はQがPのせいで動きづらくなっている(Pからの相互作用−fのため) >と考えたのですがこの理解であっているんでしょうか?
そうだと思います.もし仮に「(Pからの相互作用を+f)」としてしまうと,加えた外力よりも大きな力で運動が起こされてしまう事に成ります.こんな世界だと,エネルギーが好きなだけ取り出されてしまい,...(笑).
Re: 運動方程式の合力の向き
DIO さんのレス (2008/06/22(Sun) 11:46)
>運動方程式には向きが逆の場合
>例えば
> 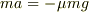 >などといったもののの場合,
>加速度の向きと合力の向きは
>一致していないと思うのです.
>(だからマイナスの符号をつけて表現しているはず)
>しかしこの運動方程式も成立します.
>などといったもののの場合,
>加速度の向きと合力の向きは
>一致していないと思うのです.
>(だからマイナスの符号をつけて表現しているはず)
>しかしこの運動方程式も成立します.
これは変じゃ無いでしょうか.この時も加速度  と合力
と合力 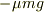 の向きも一致してます.マイナスが付くのは座標の取り方の問題だけなので
の向きも一致してます.マイナスが付くのは座標の取り方の問題だけなので
後,摩擦力の向きを決めるときは,“摩擦が無いとき物体はどの方向へ運動するか”を考え,それを妨げる向きが摩擦力の向きと考えるのが定石のように思います.
今回の場合,Qの系からみたらPは負の向きに動きます(Fの方向を正としています). ですからPには正の向きに摩擦力がかかり,Qにはその反作用として左向きに力が加わります.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/22(Sun) 17:14)
DIOさんのご指摘の;
>>例えば
>> 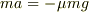 >>などといったもののの場合,
>>などといったもののの場合,
に関してコメントさせて頂きます.
この場合,進行方向に摩擦力だけが働いるだけならば,時間に伴って滑らかに変化する訳ですが,もしバネ見たいな外力が入って振動的な挙動が起こると,計算が面倒になります.
水泳でも,胴体速度は前方向きの成分だけですが,手の先の部分は後ろ向きの成分を持たないと加速出来ないので,運動方程式を解く時に,一々速度の方向をチェックするという面倒くさい事が起こります.
とすると,元々の問題では,「F」に対して「-f」と置けたのは,初期条件として箱Qや物体Pが静止していたからだと思います.その意味では,問題の完全版が知りたくなりました.
Re: 運動方程式の合力の向き
kuma(高2) さんのレス (2008/06/22(Sun) 23:55)
御解答ありがとうございます.>DIOさん
>これは変じゃ無いでしょうか.この時も加速度と合力の向きも一致してます.マ>イナスが付くのは座標の取り方の問題だけなので
よく考えてみたら自分変なこといってますね. すいません.
とすると 加速度と合力の向きは常に一致するというのが 加速度の向きだけでfの向きを判定できる根拠になるんでしょうか??
Re: 運動方程式の合力の向き
kuma(高2) さんのレス (2008/06/23(Mon) 00:05)
御解答ありがとうございます.>mNejiさん
問題の完全版についてですが この問題,設定が3回変わるため 最初の設定についての問題だけ載せますね.
(1)加速度を求めよ.
(2)PがQから受けている摩擦力の大きさfを求めよ.
(3)P,Qが一体となって運動するためには, 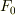 はいくら以上でなければならないか?その限界値
はいくら以上でなければならないか?その限界値 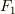 を求めよ.
を求めよ.
他の設定についても必要であれば載せます.
Re: 運動方程式の合力の向き
DIO さんのレス (2008/06/23(Mon) 00:08)
>mNejiさん
後,摩擦力の向きを決めるときは,“摩擦が無いとき物体はどの方向へ運動するか”を考え,それを妨げる向きが摩擦力の向きと考えるのが定石のように思います.
↑このことに関してでしょうか??
>kumaさん
>加速度と合力の向きは常に一致するというのが >加速度の向きだけでfの向きを判定できる根拠になるんでしょうか??
この場合に関して言えばそうですね. 水平成分にはf以外の力はかかっていませんので,fは加速度の向きになります.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/23(Mon) 02:12)
kuma(高2)さん,
私みたいに,記憶力の低い者にとって,箱(質量M)の中に小物体(質量m)が入っている,と聴くと「箱はP」その中の「物体はQ」と感じてしまうので,混乱します(笑).
>最初の設定についての問題だけ載せますね.
>
>(1)加速度を求めよ.
>(2)PがQから受けている摩擦力の大きさfを求めよ.
>(3)P,Qが一体となって運動するためには, 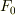 はいくら以上でなければならないか?その限界値
はいくら以上でなければならないか?その限界値 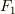 を求めよ.
を求めよ.
なるほど,出題者の意図は判って来たきがします.
やはり私の感覚からすると,静止摩擦係数と動摩擦係数とは別に,摩擦係数を定義したくなります.ここら辺は,高校教科書の説明法を理解してないので,直ぐに回答出来ません.急がれるばあい,DIOさんと論議を進めてくださいな.
>他の設定についても必要であれば載せます.
これは不要ですね.ご免なさい.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/23(Mon) 02:16)
DIOさん,
>後,摩擦力の向きを決めるときは,“摩擦が無いとき物体はどの方向へ運動するか”を考え,それを妨げる向きが摩擦力の向きと考えるのが定石のように思います. > >↑このことに関してでしょうか??
そうです.私は,水泳の計算をするうちに,運動方向の逆に「抗力=摩擦力」が働くのに気が付きました.お恥ずかしい(笑).
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/23(Mon) 15:41)
今日,予定がキャンセルになったので,検討してみました.無理矢理の感がありますが,どんなものでしょうか.
箱と物体の運動方程式は;
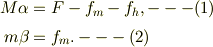
ここで,物体が箱に与える摩擦力 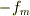 ,水平台が箱に与える摩擦力
,水平台が箱に与える摩擦力 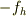 とすると;
とすると;
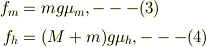
となる.ここで題意より,それぞれの摩擦係数 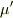 は共に,
相対的に静止していれば,
は共に,
相対的に静止していれば, 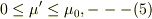 相対的に運動していれば,
相対的に運動していれば,  に従うものとする.
に従うものとする.
以下,段階的に吟味します.
■外力Fが小さくて,全体を動かせない場合■
すなわち, 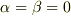 であるから,式(1),(2)より,
であるから,式(1),(2)より,
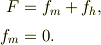
従って,静止条件の式(5)から,
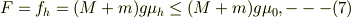
となるから,最大静止外力 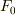 は,
は,
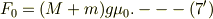
■箱は動き出すが,物体は箱に固着している場合■
すなわち, 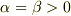 の場合.
の場合.
式(1),(2)を辺々加え,式(6)を加味すると,加速度は;
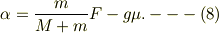
■さらに物体が箱から離れだす場合■
もはや,式(1),(2)は独立に成立する必要があります.そこで箱から見た物体の加速度, 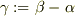 を考えると,
を考えると,
![m\gamma &= m(\beta-\alpha),\\&= f_m - \frac{m}{M}(F-f_m -f_h ),\\&= -\frac{m}{M}(F-f_h) +\frac{M+m}{M}f_m ,\\&= -\frac{m}{M}[F-(M+m)g\mu] +[1+\frac{m}{M}]mg\mu_m.](http://hooktail.maxwell.jp/bbslog/3ef934fabcc587821cc9b1088908e1e2.png)
右辺の第一項は見かけの外力を示し,第二項は見かけの摩擦力を示すと考えられます.すると,物体が静止している為には;
![\frac{m}{M}[F-(M+m)g\mu]=[1+\frac{m}{M}]mg\mu_m,](http://hooktail.maxwell.jp/bbslog/818e19d7a5723c2a7a17bec501a2d116.png)
が必要で,摩擦係数の条件(5)より外力の最大値 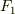 は,
は,
![F_1 &= (M+m)g\mu + [1+\frac{M}{m}]mg\mu\\&= 2(M+m)g\mu. ----(9)](http://hooktail.maxwell.jp/bbslog/260ae1dfa61dcddcfe5a86d191bcd03b.png)
◆◆◆検算はしていませんし,間違いかも知れません.◆◆◆
Re: 運動方程式の合力の向き
DIO さんのレス (2008/06/23(Mon) 17:43)
私も摩擦力の向きはたびたび間違えます.設定が複雑だとなおさら,,水泳などでは難しそうですね.
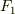 に関してはなんですが,
問題では,最初,物体と箱が一体となっている状態から,そのまま一体となり続ける力の上限を問われているように思います.
mNejiさんの回答だと,箱と物体が別々に動いている状態から,そのまま別々に動き続ける力の下限になっていると思います.
に関してはなんですが,
問題では,最初,物体と箱が一体となっている状態から,そのまま一体となり続ける力の上限を問われているように思います.
mNejiさんの回答だと,箱と物体が別々に動いている状態から,そのまま別々に動き続ける力の下限になっていると思います.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/23(Mon) 21:12)
DIOさん,
>私も摩擦力の向きはたびたび間違えます.設定が複雑だとなおさら,,水泳などでは難しそうですね.
そうですね何の因果か知れませんが,不得意な分野に手を染めてしまった様です.
> 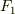 に関してはなんですが,
>問題では,最初,物体と箱が一体となっている状態から,そのまま一体となり続ける力の上限を問われているように思います.
>mNejiさんの回答だと,箱と物体が別々に動いている状態から,そのまま別々に動き続ける力の下限になっていると思います.
に関してはなんですが,
>問題では,最初,物体と箱が一体となっている状態から,そのまま一体となり続ける力の上限を問われているように思います.
>mNejiさんの回答だと,箱と物体が別々に動いている状態から,そのまま別々に動き続ける力の下限になっていると思います.
まだ良くわからないのですが, ・「相互に静止している上限」+δ=「相互に運動している下限」 もしくは ・「相互に静止している上限」=「相互に運動している下限」-δ 見たいな感じかな,と....
摩擦は魔物ですね.
Re: 運動方程式の合力の向き
DIO さんのレス (2008/06/23(Mon) 22:48)
「相互に静止している上限」>「相互に運動している下限」です. 一般に静止摩擦係数>動摩擦係数ですので
摩擦を魔擦と書くのはどうでしょう(笑
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/23(Mon) 23:34)
>一般に「相互に静止している上限」>「相互に運動している下限」です. >静止摩擦係数>動摩擦係数ですので
さきほど高校での説明が知りたくなったので,数研出版の物理Iの「摩擦や空気の抵抗を受ける運動」という項目の「図50静止摩擦力と動摩擦力」という解説を拝見しました.今回の例で言えば,質量Mの物体に,外力Fを掛けた時の摩擦力fの振る舞いを図示しています. 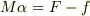 について,
について,
<pre>
摩擦力 f 静摩擦力 ←|→動摩擦力 ↑ |f=F/ |/ |/ |/ |/________f=Mgμ(一定) |/ |/ |/ + ───────・────────────→ |Mgμ_0 外力F
</pre>
といった感じです.静摩擦力と動摩擦力とにはギャップが存在しますが,対応する外力は連続的であるのが印象的だと思います.この図を高校生の時に見ていれば,摩擦についての印象が変わったかも知れません.
>摩擦を魔擦と書くのはどうでしょう(笑
言い得て妙です.水泳の解析では「魔擦」と言う表現を引用してみます.
Re: 運動方程式の合力の向き
kuma(高2) さんのレス (2008/06/24(Tue) 00:07)
返信ありがとうございます!>mNejiさん DIOさん
投稿が遅れてしまってすいません.
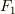 に関してなんですが
に関してなんですが
名問の森の解答では
PがQから受ける垂直抗力をRとすると,上下のつり合いから 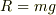 一方,静止摩擦力fは最大摩擦力
一方,静止摩擦力fは最大摩擦力 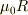 以下でなければ
ならないから
以下でなければ
ならないから
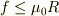
よって
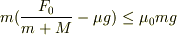
∴ 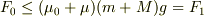
となっていて
この解答中で求められた 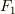 には
静止摩擦係数が含まれることから
には
静止摩擦係数が含まれることから
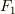 は「相互に静止している上限」になると思います.
は「相互に静止している上限」になると思います.
それにしても mNejiさんやDIOさんのような物理の出来る方が 摩擦が不得意とは意外です.
高校物理では 難易度が低めになっていますが(定石に従えば機械的に出来るからか?) 深く考えてみると 意外と摩擦は難しいんですね.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/24(Tue) 01:38)
kuma(高2)さん,
私は,まだこの分野が判っていない様です.おいおい考えたいと思います.
でも,受験の為には確りと手法をマスタされますように.
>高校物理では >難易度が低めになっていますが(定石に従えば機械的に出来るからか?) >深く考えてみると >意外と摩擦は難しいんですね.
最近,強く感じる様になったのは; 小学校の算数 <--> 高校の物理 中学校の数学 <--> 教養の物理 のような対応関係です.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/24(Tue) 08:46)
DIOさん,
> 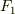 に関してはなんですが,
に関してはなんですが,
なにか操作ミスをしていたような気がします.
自己引用しますと
>右辺の第一項は見かけの外力を示し,第二項は見かけの摩擦力を示すと考えられます.すると,物体が静止している為には;
> ![\frac{m}{M}[F-(M+m)g\mu]=[1+\frac{m}{M}]mg\mu_m,](http://hooktail.maxwell.jp/bbslog/004171f17cc19f7d615d33e38a596e06.png) >が必要で,摩擦係数の条件(5)より外力の最大値
>が必要で,摩擦係数の条件(5)より外力の最大値 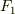 は,
は,
に続いて, 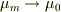 とするベキです.すると,
とするベキです.すると,
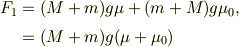
となりますね.
今ながら,動摩擦係数は明示的に,例えば, 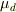 の様に示してくださると有難いですね.ーーー>出題者の皆様方.
の様に示してくださると有難いですね.ーーー>出題者の皆様方.
kumaさん,
>∴ 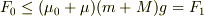
少なくとも,右側の等号は一致しました.ホッとしました.まあ,ケアレス・ミスの反面教師と思って笑っておいてください.
ですから,ある程度は定型化することでミスを低減出来ると思うべきなのでしょうね.これに懲りずに,ベストを尽くされん事を.
ただし,今回の方法では,非慣性運動をしている箱から物体を見たときの「見かけ場の運動方程式」を持ち出しましたが,自分の内心では裏が取れていません.若しくは,もう少し違う式操作も有るかも知れません.もう少し,時間をかけて検討したいと思います.
Re: 運動方程式の合力の向き
DIO さんのレス (2008/06/24(Tue) 09:57)
mNejiさんは箱と物体が離れている仮定し,そこから 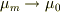 とされていますが,箱と物体が離れているとき動摩擦係数
とされていますが,箱と物体が離れているとき動摩擦係数 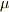 は不変ですので,この操作は良くないかと思われます.
は不変ですので,この操作は良くないかと思われます.
箱と物体が相互に運動しているとき
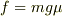 箱と物体が相互に静止しているとき
箱と物体が相互に静止しているとき
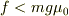
この二つは同時には考えられないかと,
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/24(Tue) 22:43)
kuma(高2)さん,
その後,No.20484にお示しした式の妥当性を検討しました.
式(1)〜(6)は妥当だと思います.更に,番号は付けていませんでしたが,
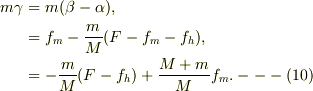
も慣性系座標でないですが,慣性座標系で求めた運動方程式からの線形変換で得た運動方程式であるので正しい運動方程式であると思うに至りました.
そこで,実際の場合分けを式(1),(10)に付いて適用すれば良いと思いました.
もしも,やって見て不都合がありましたら,ご質問下さい.
ただし,受験の実際上の技法という意味では,現在学ばれている手法に従っているほうが安全だろうと思われます.
Re: 運動方程式の合力の向き
kuma(高2) さんのレス (2008/06/25(Wed) 18:14)
>mNejiさん
>ただし,受験の実際上の技法という意味では,現在学ばれている手法に従っているほうが安全だろうと思われます.
深く考えるにしても 基礎がしっかりしてなくてはダメですもんね笑.
まずは基本的な解法や定石をマスターすることを 最優先して勉強していこうと思います.
>mNejiさん DIOさん
自分の疑問も解決したことですし 今回の質問内容に関するレスは最後にしようと思います.
丁寧な御解答,御説明本当にありがとうございました.
Re: 運動方程式の合力の向き
mNeji さんのレス (2008/06/25(Wed) 23:40)
kumaさん,
>まずは基本的な解法や定石をマスターすることを >最優先して勉強していこうと思います.
やはり,まずは大学入試を突破するという標的から目をそらさない方が善い様です.
それと高校の数学は,物理の為にもしっかりと力を貯めておいて下さい.
というのも,昨日現役の教官の方とお会いする機会があって,入試制度も含めて論議をしましたが,高校生が「微積分を駆使して問題を解くのは一向に差し支えない」とお聞きしました.また受験塾では実際にそのような運営をしているそうです.
残念ながら,公式に頼らずに自分の力で解く様なタイプの学生を選抜するようなシステムは成功していないそうです.逆に言えば,入ってしまえば,微積分を存分に駆使して,自分の道を組上げる事は可能だし,むしろその様な学生に頑張ってほしいとお聴きしました.
その意味でも,効率の良い勉強は大切だと,思います(ハクション).残念な事に,私は,物質の構造に由来する「摩擦」とか,「熱力学」などを切り捨ててきたので,こんな事を言う資格はありません.でも,最近の参考書を拝見すると,物理数学,熱力学,統計力学などにも良書を散見します.その上,この掲示版を含めて,インターネットの資料も迫力があります.
受験勉強の中でも,腑に落ちない場合があると思います.その時には多くの方々がkumaさんの疑問にお答え下さると思います.論議の勉強と思って,気楽に質問されると嬉しいです.多いにベストを尽くされます様に.