水中での空気泡の上昇速度と泡の直径との関係

水中での空気泡の上昇速度と泡の直径との関係

mNeji さんの書込 (2008/06/20(Fri) 21:52)

私は，水泳での手や足の運動にともなう推進力の起源について興味を持っています．

その関連で，バタフライのように急激に手を前方に出して水中に入れ，手を腕ごと大きく回転して行く時に，手の甲側(水中で手の進行方向の後ろ側)に泡が自動追尾するよな振る舞いが見られる事に気が付きました．

これを，プールで手を空中から水中に斜めに打ちながら，目前で観察しています．とても面白いことに，手のスピードが上がる程，泡は手の甲に追尾します．逆に手のスピードが低くなると，泡は手の甲から離れて，水面に向けて上昇してしまいます．

なぜ，泡が手の甲にトラップされるかも面白いのですが，今日お聞きしたいのは，トラップが解除された泡が「上昇する速度」と「その直径」とになにか相関が有りそうな事です．気のせいかも知れませんが，直径が大きい程，上昇速度がはやくなるようにも感じます．

これらに付いて，ご存知の事がありましたらお教え下さると嬉しいです．

また，簡単に実験する方法などのアイデアを頂けると幸いです．

Re: 水中での空気泡の上昇速度と泡の直径との関係

mNeji さんのレス (2008/06/20(Fri) 22:57)

自己コメントです．

浮力Bは体積に比例．よって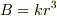， B=k r^{3}

流体の中の球体の抗力Dは断面に比例 , 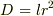D = l r^2

と考えると，定性的には半径が大きいほど上昇速度は増えそうですね．すると，ちいさな泡のほうが重力的にはトラップし易いことになります．

すると，手の甲の裏にトラップする力は，重力加速度と同程度の値を持つ可能性が示唆されます．本当だろうか ...．

内心は，表面張力が関与するような気がしていましたが．

もう少しインターネットでの検索が必要そうですね．

Re: 水中での空気泡の上昇速度と泡の直径との関係

mNeji さんのレス (2008/06/21(Sat) 15:26)

普通，泡とか液滴が物理の問題で出てくるのはミリカンの実験の油滴ぐらいだと思います．私は，水泳の計算は幾つかしていますが，気泡の上昇は，今回初めてです．まあ，質問をしてしまったのも何かのご縁でしょうから，泡が上昇する時の運動を表現してみます．

半径Rの空気の泡が，水中に出来たとします．垂直上方にz軸をとり，時刻t=0の時にz軸の原点に静止していたとします．

泡の体積，断面積を；

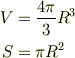
V &=\frac{4\pi}{3}R^3\\S &=\pi R^2

とします．

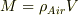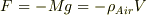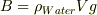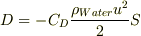
気泡の質量， M=\rho_{Air}V 重力， F = -Mg = -\rho_{Air}V 浮力， B=\rho_{Water}Vg 抗力， D= -C_{D}\frac{\rho_{Water}u^2}{2}S

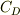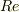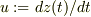
ここで， C_{D} は球体の抗力係数で，レイノルズ数， Re の関数． また，気泡の上昇速度， u := dz(t)/dt

気泡の運動方程式は，

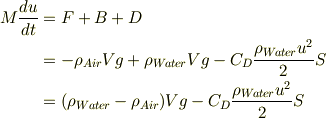
M\frac{d u}{dt} &= F+B+D \\&= -\rho_{Air}Vg+\rho_{Water}Vg-C_{D}\frac{\rho_{Water}u^2}{2}S\\&= (\rho_{Water}-\rho_{Air})Vg -C_{D}\frac{\rho_{Water}u^2}{2}S

必要に応じて，微分方程式を解くことになあります．ここでは，定常速度に達した場合を考えます．当然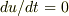， du/dt=0 だから，運動方程式の「左辺=0」を求めることになる．水の密度は空気の密度の千倍弱だから，

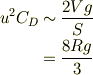
u^2 C_{D}&\sim \frac{2Vg}{S}\\&= \frac{8Rg}{3}

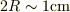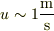
ここで，プールでの気泡の動きから，レイノルズ数の概算をしておくと, 半径， 2R \sim 1\mathrm{cm} で，速度， u \sim 1\frac{\mathrm{m}}{\mathrm{s}}

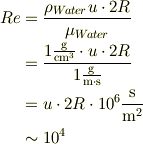
Re &= \frac{\rho_{Water} u\cdot2R}{\mu_{Water}}\\&= \frac{ 1\frac{\mathrm{g}}{\mathrm{cm^3}} \cdot u\cdot2R}{1\frac{\mathrm{g}}{\mathrm{m}\cdot\mathrm{s}}}\\&= u\cdot2R\cdot 10^6 \frac{\mathrm{s}}{\mathrm{m^2}}\\&\sim 10^4

となる．これに対応する抗力係数から終速度を求めることになります．