波の合成

波の合成

さえ さんの書込 (2008/06/20(Fri) 13:10)

大学の授業で専門ではない授業の課題に苦しんでいます．． だれか分かる方いましたら教えてください＞＜

１，次の二つの波 u=Aexp{i(kx-ωt)} v=Aexp{i(-kx-ωt)} の合成波を求めよ．

２，振幅と角振動数が等しく，進行方向が反対どうしである２つの平面波 u=Aexp{i(kx-ωt)} v=Aexp{i(-kx-ωt)} の合成派を求めよ．

３，振幅ならびに進行方向が等しく，角振動数の僅かに異なる２つの平面波 u=Aexp{i(k1x-ω1t)} v=Aexp{i(k2x-ω2t)} の合成波を求めよ．

４，振幅が等しく，波数，角振動数が異なる２つの平面波 u=Aexp{-i((ω+△ω)t-(k+△k)x)} v=Aexp{-i((ω-△ω)t-(k-△k)x)} の合成波を求めよ．また，２つの波の重ね合わせを図示せよ．

Re: 波の合成

mNeji さんのレス (2008/06/21(Sat) 16:34)

さえさん，専門でない出題にしては，主旨がわかり難い問題ですね．

＃複素数表示をどのように考えるかを教えて頂いているのですよね？

手始めに，一部を計算してみます．なお，書くのが複雑になるので，数式表現を使って書かせて頂きます．

問い１

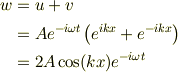
w &= u+v\\&= Ae^{-i\omega t}\left( e^{ikx} +e^{-ikx}\right)\\&= 2A\cos(kx)e^{-i\omega t}

波長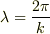， \lambda = \frac{2\pi}{k} の定在波が出来ていて，全体が時間周期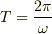， T=\frac{2\pi}{\omega} で振動している．

問い4

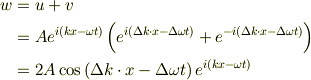
w &= u+v\\&= Ae^{i(kx-\omega t)}\left( e^{i(\Delta k\cdot x-\Delta\omega t)} +e^{-i(\Delta k\cdot x-\Delta\omega t)} \right)\\&= 2A\cos\left( \Delta k\cdot x-\Delta\omega t \right)e^{i(kx-\omega t)}

空間波長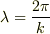， \lambda = \frac{2\pi}{k} で，時間周期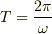， T=\frac{2\pi}{\omega} の搬送波 ; 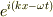e^{i(kx-\omega t)} ;がx軸の正の方向に進行している．

その振幅は，長い空間波長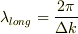， \lambda_{long} = \frac{2\pi}{\Delta k} で，長い時間周期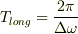， T_{long}=\frac{2\pi}{\Delta \omega} を持つし進行波(x軸の正の方向に進行している)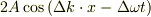； 2A\cos\left( \Delta k\cdot x-\Delta\omega t \right) ；によって変調されている．