慣性の法則の必要性
慣性の法則の必要性
DIO さんの書込 (2008/06/18(Wed) 22:25)
慣性の法則（運動の第1法則）は
外力が加わらなければ，静止している質点は静止を続け， 運動している質点は等速直線運動を続ける．
などと書かれていますが，この法則は必要なのでしょうか??
第2法則
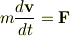
で考えると，外力が加わらないとき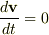 
となり，これで十分“静止している質点は静止を続け，運動している質点は等速直線運動を続ける”を言えていると思うのですが，，
Re: 慣性の法則の必要性
yama さんのレス (2008/06/18(Wed) 23:02)
確かにそのように考えることもできるので，第１法則と第２法則の関係についてはいろいろ議論のあるところですが，一般的には，第１法則は慣性系の存在を保証していると解釈されることが多いようです． すなわち，第１法則によって外力が加わらない物体が等速直線運動をするような座標系すなわち慣性系が必ず存在し，そのような慣性系において第２法則が成り立つと考えるわけです．
