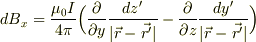ベクトルポテンシャルからビオ・サバールの法則の導出
ベクトルポテンシャルからビオ・サバールの法則の導出
えり さんの書込 (2008/06/18(Wed) 21:37)
ベクトルポテンシャルからビオ・サバールの法則を導きたいのですが,
「 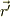 にある電流素片
にある電流素片 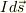 が
が 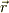 の位置につくるベクトルポテンシャル
の位置につくるベクトルポテンシャル 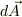 を求め,その回転をとることにより,
を求め,その回転をとることにより, 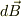 を求めよ.」
という問題で,私は
を求めよ.」
という問題で,私は
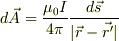 としたのですが,これは間違っていますか?(汗)
としたのですが,これは間違っていますか?(汗)
この後に回転をとろうとすると, 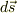 の微分でつまずいてしまったのです…
の微分でつまずいてしまったのです…
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
えり さんのレス (2008/06/18(Wed) 23:53)
返信ありがとうございます.
ということは, 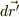 を微分すると,0になるということでしょうか?
を微分すると,0になるということでしょうか?
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
えり さんのレス (2008/06/19(Thu) 00:49)
どうもありがとうございましたm(__)m
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
mNeji さんのレス (2008/06/19(Thu) 02:04)
遅ればせながらコメントをお許し下さい.
ご質問としては完了していると思いますが,せっかく此処まで到達しているのですから,ビオ・サバールの法則までの流れを書いて見ませんか?
私は高校生のときに「ビオ・サバールの法則」を見た時に,とても胡散臭い感じがしていて,今回ご質問の関係を知って,安堵した記憶が有ります.
高校生さんや大学の1年生さん達が,上の導出をご覧に成っていれば,大学2年生の電磁気をやる意味が感じ取れるような気がするからです(笑).
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
えり さんのレス (2008/06/19(Thu) 23:52)
では,導出してみます.(高校生さんや大学1年生さんのためにも頑張ります(笑))おかしなところがあればご指摘下さい.
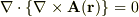 …(1)
は,任意の
…(1)
は,任意の 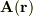 についていつでも成り立つ.
についていつでも成り立つ.
ここで静磁場の基本法則,
 より,上の関係を用いて
より,上の関係を用いて
 …(2)
が導ける.
…(2)
が導ける.
さて,以下でベクトルポテンシャルからビオ・サバールの法則を導出する.
ベクトルポテンシャル
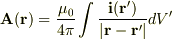 より,(2)を用いて
より,(2)を用いて 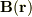 を求める.
を求める.
磁束密度のx成分を計算すると,
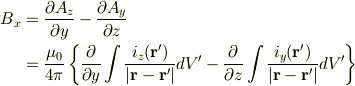
ここで,
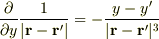
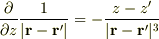 よって,
よって,
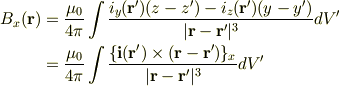
y,z成分も同様に求められるので,
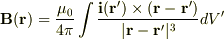 となる.
これは,ビオ・サバールの法則に他ならない.
よって示せた.■
となる.
これは,ビオ・サバールの法則に他ならない.
よって示せた.■
と,こんな感じで大丈夫でしょうか? 今度,電気双極子についての質問をしようと思っているのですが,今日はもう遅いので,それはまた後日にでも(笑) 失礼します..
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
mNeji さんのレス (2008/06/20(Fri) 01:55)
お忙しい所,お時間を取らせてしまいご免なさい,m(_._)m.でも,後輩の為になっているので,お許し下さい,:-P).
さて,大筋の流れはいいと思います.ただ, 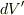 は,始めのご質問にあった,線積分
は,始めのご質問にあった,線積分 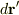 とした方が良いと思います.
とした方が良いと思います.
でもベクタ・ポテンシャルが
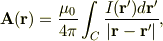
と書けるのは,静電気のスカラ・ポテンシャルの表記との対応性が明白になって感激ものですよね.ということは,現在の時点で,静電場と静磁場とを対称的に記述できている,と言えますね.
ちなみに,静電気のスカラ・ポテンシャルは,
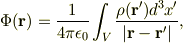
ですよね.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
DIO さんのレス (2008/06/20(Fri) 16:27)
失礼します.高校生や大学の1年生達の類です(笑
ベクトルポテンシャル 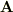 の求め方を教えていただけないでしょうか??
の求め方を教えていただけないでしょうか??
静電ポテンシャルがmNejiさんの書かれたようになるのは,ポアソンの方程式
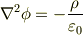
を解けばいいと理解しているのですが(これも自力では解けないのですが,,,)
ベクトルポテンシャルも同じようにできるのでしょうか?? 静磁場の基本法則から
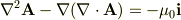
が得られたので,これを解けば良いような気がしているのですが
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
yama さんのレス (2008/06/20(Fri) 17:12)
もちろん,それを解けばいいのですが,ベクトルポテンシャルにはゲージ変換の不定性があるので,その方程式からベクトルポテンシャルを一意的に定めることはできません.
しかし,その不定性を利用してベクトルポテンシャルに適当な条件を付け加えて,方程式を簡単にすることができます.
たとえば, 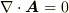 という条件がよく用いられます.そうすると方程式は次の形になります.
という条件がよく用いられます.そうすると方程式は次の形になります.
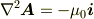
あとは静電ポテンシャルと同様に考えればいいでしょう.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
DIO さんのレス (2008/06/20(Fri) 20:36)
回答有り難うございます.
ということは 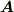 は
は
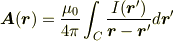
以外の形もとり得るということですよね?? でも,

に 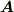 を代入すると
を代入すると 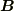 は同じになる,と.
は同じになる,と.
堂々巡りしてる気もするのですが,ポテンシャルを導入することによっていろんな計算が楽になる.ということですかね
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
mNeji さんのレス (2008/06/20(Fri) 21:21)
DIOさん,今晩は.
>失礼します.高校生や大学の1年生達の類です(笑
いやはや,本当に当時は,目から鱗が音を立てて落ちて行った気がしました.
>ベクトルポテンシャル 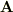 の求め方を教えていただけないでしょうか??
の求め方を教えていただけないでしょうか??
これも,yamaさんの解説があるようにゲージ不定生からベクタ・ポテンシャルがポアソンの方程式を満たします.この方程式は線形ですから,ベクタの成分ごとに独立なスカラ型のポアソン方程式と考え直すと;
>静電ポテンシャルがmNejiさんの書かれたようになるのは,ポアソンの方程式
> 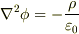 >を解けばいいと理解しているのですが(これも自力では解けないのですが,,,)
>を解けばいいと理解しているのですが(これも自力では解けないのですが,,,)
それぞれ,電流密度成分,静電気密度と由来が違うものの,計4つのポアソン方程式に従うポテンシャルが出る事になります.まさに電流と静電気が同じ土俵に乗ったと,大学の1年生も終わったころの私は思いました.
で,静電ポテンシャルをポアソン方程式から演繹的に出す話は,当時ポテンシャル論の教科書を拝見しても,素直に判らずふて腐れていました.取り敢えず点電荷によるクーロン電荷によるスケイラ・ポテンシャルから始まって,多数の点数となった近似で電荷密度分布から求められる,と納得して,さらにベクタ・ポテンシャルもその類推で与えられると納得すると,時間変動のない電場・磁場の関係はあっと言う間に構築できる,とう理解に達し....
という流れから,一種の虚脱状態に達してしまったという経験があります.;-P(
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
yama さんのレス (2008/06/20(Fri) 23:04)
DIOさんの理解で大体よいと思いますが,ベクトルポテンシャルを用いることによって見通しがよくなると言えるでしょう.
たとえば,電磁場は6個の変数 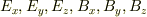 で表されますが,スカラーポテンシャルとベクトルポテンシャルで置き換えることによって,変数を
で表されますが,スカラーポテンシャルとベクトルポテンシャルで置き換えることによって,変数を 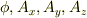 の4個に減らすことができます.
また,スカラーポテンシャルとベクトルポテンシャルをまとめた
の4個に減らすことができます.
また,スカラーポテンシャルとベクトルポテンシャルをまとめた 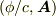 という量は,ローレンツ変換に対して4元ベクトルとして変換します.これは電磁場の成分の変換に比べて簡単です.
さらに,電磁場中の荷電粒子の一般化運動量は,ベクトルポテンシャルを用いて
という量は,ローレンツ変換に対して4元ベクトルとして変換します.これは電磁場の成分の変換に比べて簡単です.
さらに,電磁場中の荷電粒子の一般化運動量は,ベクトルポテンシャルを用いて 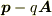 と表すことができます.
と表すことができます.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
DIO さんのレス (2008/06/21(Sat) 00:01)
>mNejiさん 初めまして,返信有り難うございます.
ビオ・サバールの法則は私の使ってたテキストではマクスウェル方程式の一つということになっていました. 今では,なんか騙されてた気もしますが,ウソとは言えないんでしょうね.
ところで今の高校の教科書にはビオ・サバールの法則自体載っておりません. 直流電流,円電流,ソレロイドの作る磁界を天下り的に載せてあるだけです. 他にも思うところがいろいろありますが,高校で習う電磁気はあまりに酷だと思います.
>当時ポテンシャル論の教科書を拝見しても,素直に判らずふて腐れていました. 私も全く同じ経験をしました(笑
>yamaさん いろいろな利点があるのですね.電磁ポテンシャル,すばらしい技巧だと思います.
しかも,先ほどベクトルポテンシャルについて検索しててアハラノフ・ボーム効果なるものを見つけたのですが,電磁ポテンシャルは単なる数学的技巧じゃなく実際に存在するのですね.
これにはビックリしました.いや,ホント電磁気はおもしろいです.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
yama さんのレス (2008/06/21(Sat) 00:35)
古典論では,あくまでも電磁場が基本であって,電磁ポテンシャルは便宜上導入された補助的なものです.
しかし,量子論になると古典論とは違って,アハラノフ・ボーム効果からわかるように電磁ポテンシャルのほうが基本的であると考える必要があります.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
mNeji さんのレス (2008/06/21(Sat) 00:39)
>ビオ・サバールの法則は私の使ってたテキストではマクスウェル方程式の一つということになっていました. >今では,なんか騙されてた気もしますが,ウソとは言えないんでしょうね.
一つの見識かも知れませんね.
>ところで今の高校の教科書にはビオ・サバールの法則自体載っておりません. >直流電流,円電流,ソレロイドの作る磁界を天下り的に載せてあるだけです. >他にも思うところがいろいろありますが,高校で習う電磁気はあまりに酷だと思います.
なるほど,載っていませんね.私は,高校の物理の教科書は試験の時に問題を見る為にしか見なかったので,どういう説明だったかも知りません(泣き).昨年,参考の為に数種類の高校物理の教科書をかって,論議があるときに所々見ていますが,なにか伝えるべき骨格がフニャフニャだと感じます.
大昔の小学校の算数の話です.鶴亀算といった技巧を教える時間を取ったものの,中学で代数が入れば,なんの事も無い話でがっかりしたものです.
最近は,グラフィックス表現を気楽に使えるので,数学をベースとした物理を系統的に,中・高・大・院までに展開する教科書作りが強く求められていると感じます.
きっと,大手の予備校さん達は,その手の企画を進行させているのでしょうが....
>当時ポテンシャル論の教科書を拝見しても,素直に判らずふて腐れていました. 私も全く同じ経験をしました(笑
丁度,この静電場・静磁場のポテンシャル表現が,マクスウェル方程式群に連なる分水嶺なような気がします.此処を通過してしまえば,一挙に動的な電場・磁場,特殊相対論等とのリンクが広がる訳ですから.こんな豊かな世界があるのに,静電場にまつわるガウスの法則を細かく解剖する必要があるのか理解に苦しみます.
という偏屈な爺さんの独り言です.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
DIO さんのレス (2008/06/21(Sat) 09:04)
>yamaさん 量子論だけの話だったんですね.誤解をしてました. いやはや,私,古典物理と現代物理の違いがよくわかってないです.というか量子論には未着手なのですが,
>mNejiさん
>最近は,グラフィックス表現を気楽に使えるので,数学をベースとした物理を系統的に,中・高・大・院までに展開する教科書作りが強く求められていると感じます. 全く同感です. 今の教科書は数学的表現をあまりしないことで物理が簡単になるとでも思ってるかのように感じます(高校数学との平衡の関係もあるのでしょうが,).高校数学で習う微積でさえ,物理には少しも顔を出していませんから.
Re: ベクトルポテンシャルからビオ・サバールの法則の導出
mNeji さんのレス (2008/06/21(Sat) 10:19)
>今の教科書は数学的表現をあまりしないことで物理が簡単になるとでも思ってるかのように感じます(高校数学との平衡の関係もあるのでしょうが,).高校数学で習う微積でさえ,物理には少しも顔を出していませんから.
私の場合,水泳の力学的説明をしようとしています.この場合,グラフを出しておけば理解してくれると思っていたら,トンでもない.結局,その結果をアニメーションにして,ようやく一部の人が納得してくれるという事が判りました.
逆に,式やグラフだけでは「概念の伝達」に不足する部分があるのも事実です.
今回の論議が発展できたのも,この「数式掲示版の数式表現の高さ」によるものだと感じます.すなわち,スケイラ・ポテンシャルとベクタ・ポテンシャルとの対応関係を「式としてのグラフィックス」の表現力を利用して明示できたからこそ,テンポ良く論議出来たのだと思います.
振り返って見れば,力学の運動方程式について,仕事の積分から保存力によるポテンシャルの導入と静電場の静電ポテンシャルの論議は,数学のツール群を系統的に準備していけば,イメージし易く,万有引力やクーロンの力を共通的に理解できますね.
その意味で,静磁場も,その関連として理解できるというのは,やはり「驚愕する事」ではないでしょうか.
更に,量子力学・特殊相論と華麗な20世紀の世界に突入するスペクタクルを堪能するには,数学を縦横に使いながらも,イメージを豊富にできるツール群の開発が大切なのかも知れませんね.
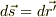 です.
です.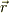 で微分することになりますが,そのとき
で微分することになりますが,そのとき