球の角運動量について
球の角運動量について
へび さんの書込 (2008/06/18(Wed) 01:45)
任意の軸に対して回転する球体の角運動量を求めたいのですが，よく分かりません.慣性モーメントは（2/5)×M×r×ｒで表すことができるということは分かったのですが，その先をどう考えればよいか分かりません.”ｚ軸周りに固定した回転”など，限定した状態ならばこの慣性モーメントに角速度をかけることで角運動量が求められるようですが，そうではなく一般的な状態での表現はどのようになるのでしょうか？
Re: 球の角運動量について
yama さんのレス (2008/06/18(Wed) 09:24)
球では，任意の軸のまわりの慣性モーメントが等しく，角運動量の向きは角速度ベクトルの向きと一致します．
従って角運動量は，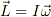 
で表されます．
球がある軸のまわりに角速度 
で回転している場合は，その軸の方向の単位ベクトルを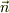 
とすると， 
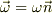なので
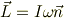
となります．
Re: 球の角運動量について
へび さんのレス (2008/06/19(Thu) 03:12)
回答ありがとうございます． 私自身の考えとして，球の三次元上での任意の位置での回転運動における角運動量を表現したいのですが，L＝(Lx，Ly，Lz)ω＝(ωx，ωy，ωz)とし，L=I×ωの関係から，L＝（Lx＝Ix×ωx，Ly＝Iy×ωy，Lz＝Iz×ωz）となるのでは？と思っているのですが，間違っているでしょうか？ちなみに，Ix＝Iy＝Iz＝2/5×M×r×rを使っています．
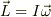と表されます．