ランダウの力学

カラビ=ヤウ空間さんの書込 (2008/06/16(Mon) 00:18)

ランダウの力学を読み始めたのですが全く分かりません．（涙 3ページ目でつまずいています・・・．

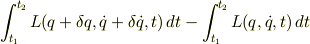
$\int_{t_1}^{t_2} L(q+\delta q,\dot{q}+\delta \dot{q},t)\,dt-\int_{t_1}^{t_2} L(q,\dot{q},t)\,dt$

の冪展開の一次の項が

どうするか詳しく教えてください．お願いします．

最初の式を計算すれば２番目の式になるということではなくて，最初の式を簡単な形に表したものが２番目の式です．あるいは，最初の式で定義されるのが２番目の式だと言ってもいいでしょう．

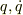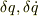作用が最小値をとるためには， $q,\dot q$ の任意の微小変化に対する作用の変化が（ $\delta q,\delta\dot q$ の１次の項までで）0でなければならないので，最初の式=0 となります．そのことを，２番目の式=0 で表すということです．

ああ，そういうこですか．ありがとうございます．分かりやすかったです．ついでに・・「変分を実行する」ってどういう意味ですか？教えてください．お願いします．

変分を実行するというのは，変分を具体的に計算することです．作用の変分を具体的に計算して，それを0に等しいと置いたものが(2-5)式です．任意の 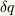$\delta q$ について(2-5)が成り立つことから，ラグランジュ方程式が導かれるわけです．

わかりました．ありがとうございます．それにしても，ランダウの力学ってわざわざ難しい表現を使っているような気がします．