二個の電子のスピン合成
二個の電子のスピン合成
メントス さんの書込 (2008/06/12(Thu) 20:51)
統計力学の院試問題です.よろしくお願いします.
2個の電子からなる原子を考える.電子のスピンを 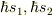 とし,その間にはハミルトニアン
とし,その間にはハミルトニアン 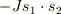 で記述される交換相互作用が働く.ただし,
で記述される交換相互作用が働く.ただし, 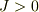 とする.電子スピン
とする.電子スピン 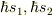 はそれぞれ磁気モーメント
はそれぞれ磁気モーメント 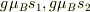 をもつ.
(1)原子の全スピンを
をもつ.
(1)原子の全スピンを 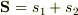 とし,その大きさを
とし,その大きさを  とする.このとき,
とする.このとき,  の値と対応するエネルギー,準位の縮退度を求めよ.
問題はまだまだ続くのですが,スピンが苦手でいきなり良く分かりません.
雑多な質問になってしまうのですが,自分なりに,スピンに関して必要だと思う知識をまとめると
1,
の値と対応するエネルギー,準位の縮退度を求めよ.
問題はまだまだ続くのですが,スピンが苦手でいきなり良く分かりません.
雑多な質問になってしまうのですが,自分なりに,スピンに関して必要だと思う知識をまとめると
1, 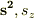 の固有値はそれぞれ
の固有値はそれぞれ 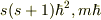 である.
である. 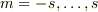 である.
2,合成に関して,
である.
2,合成に関して, 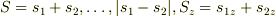
分からないことは,
1,問題文で,「電子のスピンを電子のスピンを 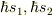 とし」とありますが,単に「スピン」と言われたら,それは大きさのことを表すと考えるのでしょうか?しかし,大きさならば,
とし」とありますが,単に「スピン」と言われたら,それは大きさのことを表すと考えるのでしょうか?しかし,大きさならば, 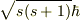 なのではないでしょうか?
また,大きさを
なのではないでしょうか?
また,大きさを 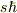 と考えると,
と考えると, 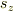 の絶対値ということになりますけど,スピンの向きはz軸と一致しない場合はないのでしょうか?
2,電子の場合,
の絶対値ということになりますけど,スピンの向きはz軸と一致しない場合はないのでしょうか?
2,電子の場合, 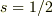 ですけれど,問題に何も書いてありませんが,勝手に
ですけれど,問題に何も書いてありませんが,勝手に 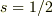 として計算を進めていっても良いのでしょうか?
として計算を進めていっても良いのでしょうか?
スピンの概念が良く分かっていないので,へんなことを言ってるかもしれませんがお願いします.
Re: 二個の電子のスピン合成
mNeji さんのレス (2008/06/12(Thu) 21:13)
メントスさん,初めまして.怒濤のごとくの質問で,気持ちが善いですね.
問い1
全スピンの固有値S=(1,0)を取りますね.全スピンの自乗の大きさは, 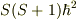 と書いた方がしっくり来るかも知れませんね.「小文字のs」だと個々の電子のスピン見たいに感じる気もします.同じ事で,全スピンのz方向への射影も「大文字のM」の方が善いかも知れません.
と書いた方がしっくり来るかも知れませんね.「小文字のs」だと個々の電子のスピン見たいに感じる気もします.同じ事で,全スピンのz方向への射影も「大文字のM」の方が善いかも知れません.
ま,定義を確りして使えばなんでも善いかも知れませんが.
問い2
電子でも,核子でも,フェルミオンで,スピン1/2は暗黙の了解で計算を進めていいと思います.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/12(Thu) 22:04)
mNejiさん,はじめまして.こんなに早く返信がつくとは思わなかったので, 質問を少し修正してしまいました. >初めまして.怒濤のごとくの質問で,気持ちが善いですね. 質問ばかりですみません^^; 院試の勉強をしていると,今まで自分が避けていた分野とかが出てきて 良い復習になるとともに,自分がいかに理解していなかったかを痛感します.
問い1に関して
少し書き方が悪かったので伝わらなかったのかもしれませんが,質問は
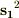 の固有値が
の固有値が 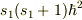 ならば,スピンの大きさ
ならば,スピンの大きさ 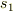 の固有値は
の固有値は 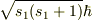 なのではないか?ということです.
問題文の「電子のスピン
なのではないか?ということです.
問題文の「電子のスピン 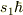 」というのは,スピンの大きさではない量なのでしょうか?
」というのは,スピンの大きさではない量なのでしょうか?
問い2に関しては理解しました.S=(1,0)になるのも大丈夫です.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/12(Thu) 22:53)
スピン(の大きさ)というのは,普通は 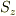 のとりうる最大値,すなわち
のとりうる最大値,すなわち 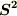 の固有値を
の固有値を 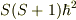 としたときの
としたときの 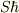 のことです.あるいは
のことです.あるいは  を指すこともあります.
ただし,これは便宜上の言い方であって,理論的にはスピンの大きさは
を指すこともあります.
ただし,これは便宜上の言い方であって,理論的にはスピンの大きさは 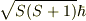 であると考えたほうがいいでしょう.
であると考えたほうがいいでしょう.
Re: 二個の電子のスピン合成
mNeji さんのレス (2008/06/13(Fri) 00:11)
>こんなに早く返信がつくとは思わなかったので, >質問を少し修正してしまいました.
丁度,運動して帰って来た所だったので,タイム・スタンプを確認せずに書いてしまいました.おっちょこチョイなのでお許しを.
>>初めまして.怒濤のごとくの質問で,気持ちが善いですね. >質問ばかりですみません^^;
横で拝見していても,確りした論議を展開されていて,一観衆としても興味深いですよ.
>院試の勉強をしていると,今まで自分が避けていた分野とかが出てきて >良い復習になるとともに,自分がいかに理解していなかったかを痛感します.
私は,凄い歳になって理解できました.お若い時には,広い分野に視野を広げて歩んでいくのが自然なのでしょうね.
定義については yamaさんの通りでしょうが,ラベルとしての「S」には「hバー」は付けない方が簡潔と思います.
他方,ハミルトニアンにスピンの自乗項があれば, 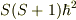 でしょうし,その絶対値と言われれば
でしょうし,その絶対値と言われれば 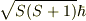 でしょうね.その意味では,文脈によって使い分けているのではないでしょうか.
でしょうね.その意味では,文脈によって使い分けているのではないでしょうか.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/13(Fri) 00:23)
>すなわち 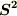 の固有値〜のことです.
の部分が良く分からないです.
の固有値〜のことです.
の部分が良く分からないです.
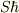 ではない残りの
ではない残りの 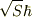 は何を表すのでしょうか?
は何を表すのでしょうか?
>mNeji ラベルというのは,固有値の量子数のことですか?
PS, yamaさん,以前質問した波動関数の時間発展の記事ですが,返信しておいたので,できたら答えをチェックしていただけると嬉しいです.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/13(Fri) 01:44)
の固有値が
でないのは,
のときでも角運動量の方向が確定していないことを意味していると思います.
波動関数の時間発展についての質問ですが,答は合っていると思います.
Re: 二個の電子のスピン合成
mNeji さんのレス (2008/06/13(Fri) 10:02)
> 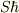 ではない残りの
ではない残りの 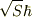 は何を表すのでしょうか?
は何を表すのでしょうか?
演算子と固有値が似た記号なので,パット目に混乱するので,あえてスピン演算子を通常のヴェクタ表示にしてみます.ある角運動量ヴェクタを 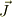 とすると,
とすると, 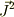 と,ある一つの座標方向の射影成分
と,ある一つの座標方向の射影成分 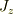 とは交換するものの,たの成分とは同時に交換性を満たさないのが,全ての始まりだったと思います.
とは交換するものの,たの成分とは同時に交換性を満たさないのが,全ての始まりだったと思います.
そこで, 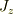 の固有値をMとすると,z方向の角運動量の射影は
の固有値をMとすると,z方向の角運動量の射影は 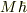 となり,その最大値
となり,その最大値  の状態から始まって,下降演算子によって数珠繋ぎに他の状態を導くことで,角運動量を表す一組の係数が決まるというのが大雑把な流れだったと思います(量子力学の本がないのでうろ覚え).
の状態から始まって,下降演算子によって数珠繋ぎに他の状態を導くことで,角運動量を表す一組の係数が決まるというのが大雑把な流れだったと思います(量子力学の本がないのでうろ覚え).
で,ある  にたいして許される角運動量の固有値
にたいして許される角運動量の固有値 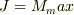 となる状態の角運動量の自乗の固有値を求めてみると
となる状態の角運動量の自乗の固有値を求めてみると 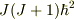 となる.そこで,各運動量の固有値状態を表す波動関数を「J,M」でラベルを貼って表す,
となる.そこで,各運動量の固有値状態を表す波動関数を「J,M」でラベルを貼って表す, 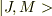 とか
とか 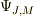 とか書くのではないでしょうか.
とか書くのではないでしょうか.
>残りの 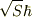 は何を表すのでしょうか?
は何を表すのでしょうか?
私は,このような表現に遭遇した記憶がありません.ヒョットして古典論への近似の論議で,大きなSの時に,角運動量の絶対値が 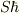 に接近するとか....
に接近するとか....
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/14(Sat) 10:02)
>波動関数の時間発展についての質問ですが,答は合っていると思います. ありがとうございました!
お二人のおっしゃっていることは同じで,要するに不確定性関係があるので,スピンの一つの方向を決めてしまうと,他の成分が確定しないということですね.すっかり忘れてしまっていました.
実際には不確定なんだけど,問題を考えるときはスピンの大きさ= 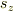 の大きさと考えてよい,ということでしょうか?
の大きさと考えてよい,ということでしょうか?
問題文の全スピン 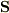
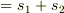 の大きさ
の大きさ  なのですが,この合成は完全にスピンがz方向のみを取ると考えて計算しても問題ないのでしょうか?
つまり,
なのですが,この合成は完全にスピンがz方向のみを取ると考えて計算しても問題ないのでしょうか?
つまり, 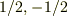 の組み合わせで0になるか,
の組み合わせで0になるか, 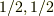 の組み合わせで1になるかでS=0,1になるわけですが,
本来は
の組み合わせで1になるかでS=0,1になるわけですが,
本来は 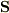 はベクトル量なので,方向の確定していないベクトル量
はベクトル量なので,方向の確定していないベクトル量 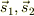 を合成した後に,絶対値をとって大きさを求めないといけないはずだと思います.(mNejiさんを真似して,ベクトルということを強調したい文字に矢印をつけてみます.)
しかし,「,
を合成した後に,絶対値をとって大きさを求めないといけないはずだと思います.(mNejiさんを真似して,ベクトルということを強調したい文字に矢印をつけてみます.)
しかし,「, 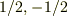 の組み合わせで0になるか,
の組み合わせで0になるか, 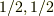 の組み合わせで1になるかでS=0,1」ということは
の組み合わせで1になるかでS=0,1」ということは 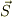 の大きさ
の大きさ  は
は 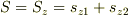 ということになりますね.
つまり,スピンはz軸に対して,上向きか下向きかの2パターンで,合成されたベクトルもz軸と平行である,ということを勝手に仮定しているように思うのですが.
方向が確定しないことを考慮した
ということになりますね.
つまり,スピンはz軸に対して,上向きか下向きかの2パターンで,合成されたベクトルもz軸と平行である,ということを勝手に仮定しているように思うのですが.
方向が確定しないことを考慮した 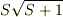 はどこへ言ってしまったのでしょうか?
はどこへ言ってしまったのでしょうか?
まとまりのない文章ですみません.自分でも混乱しています.
Re: 二個の電子のスピン合成
mNeji さんのレス (2008/06/14(Sat) 17:37)
以下に書く事は,超うろ覚えな事ですので,ちょっとした道草と思って下さい.
いま古典的な2電子系があって,その相互作用が各スピンの内積, 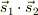 で有る様な場合を考えます.系にスピンをかく乱する摂動がなければ,全スピン
で有る様な場合を考えます.系にスピンをかく乱する摂動がなければ,全スピン 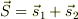 も保存する筈です.
も保存する筈です.
とすると,全スピンの辺々の内積をとると,
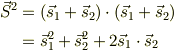
ですから,量子力学的には
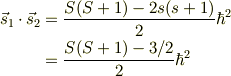
とイメージするとか....
大昔に親友と,この論争の為に授業を2コマさぼった事を思い出しました.
〜〜〜〜 なお日頃からyamaさんのご解説を拝見していると,上に書いた親友の論議ととても似ていると感じています.物理を「精密で,かつ,簡潔」に観照する立場を貫かれていて素晴らしいです.でも,たまには「アバウトで,かつ,ギクシャク」しながら物理を観賞するのも楽しいものですよ.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/14(Sat) 23:44)
スピンの合成では,スピンがz方向を向くことは仮定されていません.
合成したスピンの大きさは,2つのスピンベクトルのなす角度によって決まります.
これを直観的に理解するには古典論の場合に対応させて考えると分かりやすいでしょう.
2つのベクトル 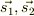 を合成したベクトル
を合成したベクトル 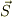 の大きさは,2つのベクトルのなす角度を
の大きさは,2つのベクトルのなす角度を  とすると
とすると
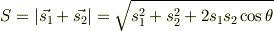
となります.従って  は,
は,  の値に応じて次の範囲の値を連続的にとることができます.
の値に応じて次の範囲の値を連続的にとることができます.
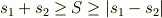
ところが,量子論ではスピンの大きさは, 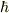 間隔の離散的な値しかとりません.従って
間隔の離散的な値しかとりません.従って  が,
が, 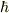 単位で表したスピンの大きさだとすると
単位で表したスピンの大きさだとすると  は次のいずれかの値をとることになります.
は次のいずれかの値をとることになります.
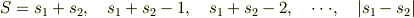
次に 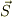 のz成分は,古典論では,
のz成分は,古典論では, 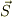 とz軸とのなす角度を
とz軸とのなす角度を  として
として 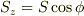 となり,
となり,  の値に応じて
の値に応じて 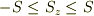 の範囲の値を連続的にとりますが,量子論ではこの範囲で
の範囲の値を連続的にとりますが,量子論ではこの範囲で 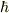 間隔の離散的な値をとることになります.
間隔の離散的な値をとることになります.
以上の説明では,スピンの大きさを( 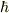 を単位として)
を単位として)  と考えました.量子論ではではスピンの大きさは理論的には
と考えました.量子論ではではスピンの大きさは理論的には 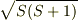 とすべきですが,平均のスピンの方向の成分が
とすべきですが,平均のスピンの方向の成分が  となるため,普通は便宜上
となるため,普通は便宜上  をスピンの大きさとしています.そうすると上記のように古典論とうまく対応させて考えることができるわけです.
をスピンの大きさとしています.そうすると上記のように古典論とうまく対応させて考えることができるわけです.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/24(Tue) 00:21)
返信おそくなって大変申し訳ありません!
yamaさんの説明を読んで,自分なりに考えてみたのですが,つまり
・スピンは方向が確定しない.だから,スピンの方向が一番z軸に近いときをスピンの大きさとみなす.(=スピンの大きさは 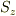 の最大値)
・スピンの合成も同じように考える.方向が確定しないので,なす角が最大のときと最小のときをスピンの大きさとする.そのあいだの中途半端なやつは量子的に考えてありえないということですね.
ということでよろしいでしょうか?どこか間違っていたらご指摘おねがいします.
「方向が確定しない」というところが,実際のSの固有値とのズレを生み出してしまうのですね.
そのズレは無視しても,計算などで困ったりすることは無いんでしょうか?
の最大値)
・スピンの合成も同じように考える.方向が確定しないので,なす角が最大のときと最小のときをスピンの大きさとする.そのあいだの中途半端なやつは量子的に考えてありえないということですね.
ということでよろしいでしょうか?どこか間違っていたらご指摘おねがいします.
「方向が確定しない」というところが,実際のSの固有値とのズレを生み出してしまうのですね.
そのズレは無視しても,計算などで困ったりすることは無いんでしょうか?
それと,もう一つ.
交換相互作用なのですが,スピンの内積 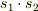 の計算を問題集で調べてみたところ,ちゃんと
の計算を問題集で調べてみたところ,ちゃんと 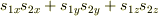 として,昇降演算子などを使って計算していたのですが
として,昇降演算子などを使って計算していたのですが
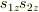 で計算してはいけないのでしょうか?
で計算してはいけないのでしょうか?
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/25(Wed) 00:21)
イメージとしてはそのように理解できると思います.
ただし,これは便宜的に考えた古典論的なイメージであって,実際の計算は,当然ながら交換関係などを用いて量子論的に行う必要があります.
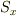 の最大値を
の最大値を  とするとき,
とするとき, 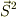 の固有値はあくまでも
の固有値はあくまでも 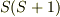 としないといけません.もしこれを
としないといけません.もしこれを 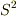 とすれば当然ながら正しい計算結果は得られません.
とすれば当然ながら正しい計算結果は得られません.
スピンの内積はスカラーでなければならないので, 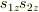 で計算することはできないでしょう.
で計算することはできないでしょう.
ところで,朝永振一郎「スピンはめぐる」の新版が最近出版されましたが,背後にある考え方や歴史的背景なども含めてスピンについて理解を深めるのに役立つと思います.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/25(Wed) 12:55)
ありがとうございます.
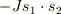 はどのように計算すればいいのでしょうか?
アップをa,ダウンをbとして
はどのように計算すればいいのでしょうか?
アップをa,ダウンをbとして 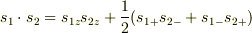 に,状態
に,状態 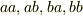 を作用させてみたのですが,
を作用させてみたのですが, 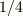 は出てきたのですけれど,
は出てきたのですけれど, 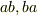 は固有方程式にならなくて固有値が求まりませんでした.両辺を足して無理やり固有値方程式を作ると
は固有方程式にならなくて固有値が求まりませんでした.両辺を足して無理やり固有値方程式を作ると 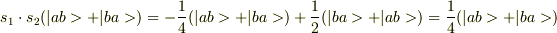 となり,期待していた結果を違う答えになってしまいました.
そもそも,
となり,期待していた結果を違う答えになってしまいました.
そもそも, 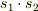 は演算子なのか?という疑問もあります.
は演算子なのか?という疑問もあります.
大きさの合成を求めるときに古典論的なイメージで考えたように
単純に平行のときに 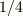 (縮退は2),反並行のときに
(縮退は2),反並行のときに 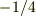 (縮退は2)とやってはいけないのでしょうか?
(縮退は2)とやってはいけないのでしょうか?
*ご紹介していただいた本,今度さがしてみます.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/25(Wed) 18:09)
mNejiさんがNo.20370に書かれているように, 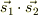 の固有値は
の固有値は 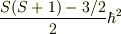 です.
です.
 の可能な値は1と0なので,それぞれの場合の固有値として
の可能な値は1と0なので,それぞれの場合の固有値として 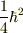 と
と 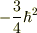 が得られます.
が得られます.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/25(Wed) 20:24)
見落としていました.すみません.ここで固有値 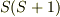 を使うのですね.
を使うのですね.
確認なのですが,今まで出てきた  や
や 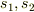 は,本当は全て演算子ですよね?普通の数字のように扱ってるのは,状態ベクトルを省略しているだけですよね?
は,本当は全て演算子ですよね?普通の数字のように扱ってるのは,状態ベクトルを省略しているだけですよね?
それと,なぜ,私の昇降演算子を使う方法だと 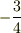 が出てこなかったのでしょうか?
が出てこなかったのでしょうか?
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/26(Thu) 01:11)
>確認なのですが,今まで出てきた  や
や 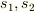 は,本当は全て演算子ですよね?普通の数字のように扱ってるのは,状態ベクトルを省略しているだけですよね?
は,本当は全て演算子ですよね?普通の数字のように扱ってるのは,状態ベクトルを省略しているだけですよね?
その通りです.
>それと,なぜ,私の昇降演算子を使う方法だと 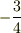 が出てこなかったのでしょうか?
が出てこなかったのでしょうか?
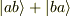 は,
は,  のときの固有関数です.
のときの固有関数です.
 のときの固有関数は
のときの固有関数は  であり,このときの
であり,このときの 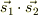 の固有値を昇降演算子を用いて求めれば
の固有値を昇降演算子を用いて求めれば 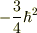 になります.
になります.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/26(Thu) 15:52)
ちゃんと同じ答えになって安心しました. しかし,固有値だけを知りたいなら,わざわざ昇降演算子を使って面倒な計算をする必要はなかったのですね.
続きの問題なのですが(本当は統計力学の問題なんです)
2,このような原子N個が温度Tで熱平衡状態にあるときの比熱を求め,低温 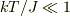 ,
, 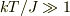 での振る舞いを議論し,比熱の温度依存性を図示せよ.
3,さらに,原子にz軸方向の磁場Hを加えたときを考える.原子のエネルギー準位を求めよ.
4,この原子N個が温度Tで熱平衡状態にあるときの磁化Mを求めよ.特に,H→0では,磁化Mは磁場Hに比例する.
での振る舞いを議論し,比熱の温度依存性を図示せよ.
3,さらに,原子にz軸方向の磁場Hを加えたときを考える.原子のエネルギー準位を求めよ.
4,この原子N個が温度Tで熱平衡状態にあるときの磁化Mを求めよ.特に,H→0では,磁化Mは磁場Hに比例する.
<自分の答え>
まず,原子一個の分配関数は 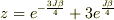 内部エネルギーは
内部エネルギーは 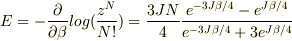 比熱は
比熱は
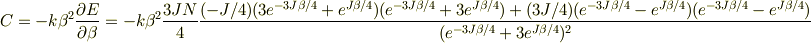
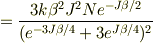
となりました.eが対称でなく,ハイパボリックが使えなくて煩雑になったのですが,最終結果の次元的には合ってるような気がします.
高温では 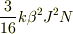 ,低温では
,低温では  になりました.
になりました.
外部磁場のある場合について,ハミルトニアンは
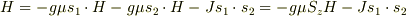 となるので
となるので
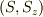 と表わすことにすると
と表わすことにすると
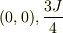
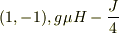
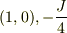
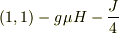 というエネルギー準位になり
一原子の分配関数は
というエネルギー準位になり
一原子の分配関数は 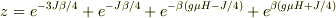 となり
磁化は
となり
磁化は
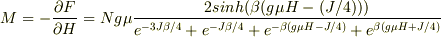 とても複雑な形になってしまいました.自信ありません.
Hが0に近いときの磁化率はどのように出すのでしょうか?
とても複雑な形になってしまいました.自信ありません.
Hが0に近いときの磁化率はどのように出すのでしょうか?
とても長くなってしまい,申し訳ありませんが どうか添削よろしくおねがいします.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/27(Fri) 22:32)
計算が面倒そうなので躊躇していましたが,一応チェックしてみました.
問2と3は,たぶん合っているだろうと思います.(見落としがあるかもしれませんが)
4の磁化の計算ですが,分子が間違ってはいないでしょうか?
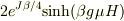 になるのではないかと思いますが.
それと,
になるのではないかと思いますが.
それと, 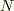 が単位体積当たりの原子数ならそれでいいと思いますが,そうでなければ体積で割る必要があると思います.
が単位体積当たりの原子数ならそれでいいと思いますが,そうでなければ体積で割る必要があると思います.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/28(Sat) 18:38)
大変な計算を頼んでしまってすみません. ほんとうに助かります.ありがとうございます.
磁化のところなのですが,計算し直したところ,ご指摘のとおり,分子の2項目のeが間違っていました.分子の 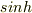 のなかも間違っていました.
H→0にすると,分子は綺麗に1になって,
のなかも間違っていました.
H→0にすると,分子は綺麗に1になって,
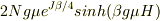 になりました.yamaさんの答え,
になりました.yamaさんの答え, 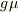 は書き忘れですよね?
は書き忘れですよね?
磁化が単位体積あたりの磁気モーメントということは分かっていたのですが,問題文に体積が与えられていません. 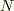 で割って,原子あたりの磁気モーメント=磁化でも良いのでしょうか?
で割って,原子あたりの磁気モーメント=磁化でも良いのでしょうか?
それと,H→0にしたとき,分母は1になって有限の値ですが,分子は0になってしまいます.これはマクローリン展開をすればよいのでしょうか?
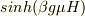 をマクローリン展開すると,磁化は
をマクローリン展開すると,磁化は
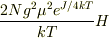 となります.
問題文のところに,弱磁場極限では,磁化は磁場に比例し,磁化率はTに依存すると書いてあったので,あってるような気はしますが.
ただ,分母は正確にH=0としたのに,分子はマクローリン展開という別々の操作をして良いのかな?と疑問に感じます.2の比熱のところもそうでしたが,いまいち極限での近似方法が分からないです.
となります.
問題文のところに,弱磁場極限では,磁化は磁場に比例し,磁化率はTに依存すると書いてあったので,あってるような気はしますが.
ただ,分母は正確にH=0としたのに,分子はマクローリン展開という別々の操作をして良いのかな?と疑問に感じます.2の比熱のところもそうでしたが,いまいち極限での近似方法が分からないです.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/28(Sat) 23:31)
となっているところが正しくは
ではないかという意味で書いたわけです.
従ってもちろんこれに 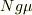 を掛けることになります.
を掛けることになります.
おそらく 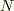 は単位体積の原子数ではないかと思いますが,はっきり書いてないのは問題の不備かもしれませんね.
原子当たりの磁気モーメントを磁化とはあまり言わないように思います.
は単位体積の原子数ではないかと思いますが,はっきり書いてないのは問題の不備かもしれませんね.
原子当たりの磁気モーメントを磁化とはあまり言わないように思います.
磁化の式でHが小さいときの近似としては,分母と分子のそれぞれをHの冪級数に展開してそれぞれ最低次の項をとればよいと思います. そうすると,分母は0次が最低なので,単に H=0 と置いたものになります.(しかし1にはならないと思いますが) 分子には0次の項がないので,1次の項をとることになります.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/29(Sun) 00:22)
>ではないかという意味で書いたわけです. 勘違いでした.すみません.
>原子当たりの磁気モーメントを磁化とはあまり言わないように思います. それでは,勝手にNを体積あたりの原子数ということにします.
近似に関してですが 0次の近似が0を代入したもの,と考えればいいわけですね. 納得しました. しかし,分母と分子で近似の程度が違っても良いのでしょうか? よく,「〜〜次までの精度で近似せよ」みたいな問題があるので,分母と分子で近似のレベルが違うのはなんとなく気持ち悪い感じがします. 分母も1次までの近似をした(たまたま0次でおしまいになったというだけで)ということで,全体としても1次までの近似をとった.と考えれば良いのでしょうか.
分母ですが
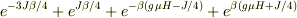 で,H=0として
で,H=0として
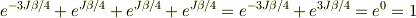
になりませんか?
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/29(Sun) 00:44)
分子と分母に分けないで,全体を冪級数に展開して最低次の項をとっても同じ結果になります. つまり,級数展開の式
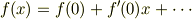
で 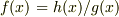 と置くと次のようになります.
と置くと次のようになります.
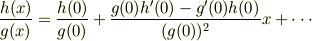
従って 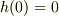 のときは次のようになるわけです.
のときは次のようになるわけです.
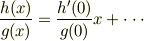
分母の計算ですが,メントスさんの計算のようにはならないと思います.
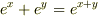 は一般には成り立ないからです.(
は一般には成り立ないからです.( 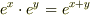 は成り立ちますが)
は成り立ちますが)
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/29(Sun) 14:11)
こういう初歩的な勘違いをよくしてしまうんですよねぇ・・・. 気をつけないと・・・.
Hの1次までの近似で
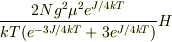 これで大丈夫でしょうか.
これで大丈夫でしょうか.
少し本筋からはずれるのですが,2つ疑問があります.
1,2問目で,比熱が低温では0というふうになりましたが,それは温度をあげても内部エネルギーが増加しない系ってことですよね?それってどういうことなのでしょうか?統計力学は結果まで行きついても物理的な意味がわからなくて苦手です.
2,一粒子の分配関数をzとしたとき,N個の系の分配関数は 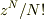 となります.N!は同種類の粒子が区別できないことを考慮したファクターであったと理解しているのですが,マクロな熱力学量にするとき
となります.N!は同種類の粒子が区別できないことを考慮したファクターであったと理解しているのですが,マクロな熱力学量にするとき 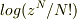 を微分することが多いので,消えてしまいますよね.あんまり意味がないような気がするのですが.
を微分することが多いので,消えてしまいますよね.あんまり意味がないような気がするのですが.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/29(Sun) 15:13)
分母は 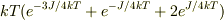 になると思います.
さらに分子分母を
になると思います.
さらに分子分母を 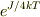 で約分するといいかもしれません.
で約分するといいかもしれません.
疑問についてですが
1. 温度と内部エネルギーの関係をグラフで表すと,グラフの接線の傾きが原点では0になるということです. T→0 のときに比熱が0に近づくことは,熱力学第3法則からも一般的に言えることです.
- N!がいつも微分で消えるわけではなく,エントロピーの計算ではN!は消えません.
Re: 二個の電子のスピン合成
メントス さんのレス (2008/06/29(Sun) 15:45)
>分母は になると思います.
おそらく,No.20524の分配関数をみて計算してくださったのかと思うのですが,
二項目の 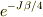 は
は 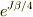 の間違いです.私が符号の間違いをしていて,それを修正して計算したのがNo.20563です.
の間違いです.私が符号の間違いをしていて,それを修正して計算したのがNo.20563です.
T→0というのは,T=0と殆ど同じ意味ですか?低温の近似ということで,もっと幅のある範囲だと思っていました. 温度とエネルギーのグラフは,原点で傾きが0で,だんだん立ち上がってきて,一定の傾きになるわけですね.
>2. N!がいつも微分で消えるわけではなく,エントロピーの計算ではN!は消えません. そうですね. やっぱり重要なファクターなんですね.
Re: 二個の電子のスピン合成
yama さんのレス (2008/06/29(Sun) 16:59)
確かに符号が間違っていましたね.私も見落としていました.
約分すれば 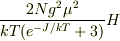 になりますね.
になりますね.
>T→0というのは,T=0と殆ど同じ意味ですか?低温の近似ということで,もっと幅のある範囲だと思っていました.
T→0というのは,T=0と殆ど同じ意味だと思いますが,低温での近似という場合は幅があると思います.
>温度とエネルギーのグラフは,原点で傾きが0で,だんだん立ち上がってきて,一定の傾きになるわけですね.
一定の傾きになるとは限りません.本問の場合は高温では傾きが小さくなるようです.