ゆーと さんの書込 (2008/06/12(Thu) 01:07)

質問し直します．dn/n = 4πvｒ^2(m/2πkT)^3/2exp(-mv^2/2kT) = F(v)dvで与えられる関数をMaxwellの速度分布則ということを調べてみたのですが，上の式を求めるにあたり，「エネルギーEとE+dEの間にある粒子数dnが「dn = n(E)dE = f(E)z(E)dE」でありf(E)はボルツマン分布関数・z(E)dEは状態密度関数と書かれています（大学が独自に作った教科書です）． まず，「ボルツマン分布関数とは簡単に言うと何なのか？」「状態密度関数とは何なのか？」「それらはなぜdn = n(E)dE = f(E)z(E)dEと書けるのか？」予習しようと検索したりしてみたものの，その分野の知識は乏しいためよくわかりません． 上のことを学ぶ上で必要な知識が得られる参考書（読みやすい・図があるなどの初心者向けの参考書）も教えていただけたら幸いです．

toorisugari no Hiro さんのレス (2008/06/12(Thu) 01:22)

「ボルツマン分布関数とは簡単に言うと何なのか？」

ある温度のときに気体分子や導体中の電子がどのようなエネルギーをもつか，あるいは平均(2乗)速度と温度にどのような関係があるか，などを記述するものです．

分布関数とはある範囲に「何か」が存在する確率をその範囲の大きさで割った密度(確率密度)です．

ゆーと さんのレス (2008/06/12(Thu) 01:30)

ある成績を取っているひとが一番多いところは盛り上がって，それよりも成績の高い人の分布は段々と下がっていって，，，，，分布関数は分かりにくいかもしれないんですが「海抜0メートルから山を頂上3000メートルまで上って，その頂上から海抜100メートルの陸地まで下るようなイメージかなと思ったのですが違いますか？それとも放物線のような山なりのような？

toorisugari no Hiro さんのレス (2008/06/12(Thu) 01:41)

> ある成績を取っているひとが一番多いところは盛り上がって

いい説明でなかったので取り消した部分なんですが．．．．

ある温度で電子(あるいは気体分子)の速度(のx成分)が 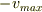(ぐらい)から 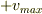(ぐらい)の間に分布しています． 数の多いのは0付近で，0から離れるにつれて数は減りますが，全体の形は裾のある洋風の釣鐘型に近い形です．(正規分布，あるいはガウス分布はご存知ですか?)

温度が高くなると 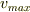も大きくなり，分布も(釣鐘型ですが)変化します．(分布が平べったく横に広がります)

そういうことを記述してるのです．(3方向の分布を掛け算にして，さらに軸座標で書き直しているので少しややこしいですが．)

ゆ―と さんのレス (2008/06/12(Thu) 07:38)

返信遅くなりましたが，なんとなくですがイメージ出来てきました． 『マクスウェル速度分布則・ボルツマン分布則』について入門用の本はありますでしょうか？またご存知でしたら何冊か紹介して頂けると嬉しいのですが． 手元にある参考書は『電気学会大学講座 電子物性基礎 (電気学会)』ですが難しいと感じています．