自重でのばね振り子の周期
自重でのばね振り子の周期
シュレディンガー さんの書込 (2008/06/11(Wed) 00:01)
高校でのばね振り子の実験で先生が,重りをつけてない時の ばね振り子の周期は,重りをつけてる時の何倍かと聞かれて今そのことで 悩んでいます. 先生のヒントは「ばね定数k,質量mのばねを水平な滑らかな台に置いた時自然長がLであった. 問1,このばねを鉛直につるしたら,いくらの長さになるか求めなさい. 問2,上の結果は,ばね定数k,質量ゼロのばねにいくらの質量の物体をつるした 場合に相当するか?」というのが先生のヒントです. 積分を使うそうです.どうか高校生の自分に教えてください.お願いします.
Re: 自重でのばね振り子の周期
yama さんのレス (2008/06/11(Wed) 14:28)
問1が分かれば問2も分かると思いますので,問1について説明します.
ばねに加わる力とばねの伸びの関係は
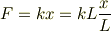
となります.
ここで 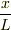 は,ばねの自然長に対する伸びの比ですが,ばねの伸びが一様である場合は,ばねの微小部分
は,ばねの自然長に対する伸びの比ですが,ばねの伸びが一様である場合は,ばねの微小部分 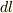 に対する伸び
に対する伸び 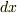 の比
の比 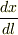 も同じになるので
も同じになるので

となります.
ばねに働く力が一様でなければ,伸びも一様でなくなりますが,それぞれの微小部分にはたらく力を  とすると,やはり(1)が成り立つと考えられます.
とすると,やはり(1)が成り立つと考えられます.
従って,おもりをつけないばねをつるしたとき,下端から自然長で 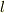 から
から 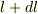 までの部分
までの部分 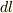 の伸びを
の伸びを 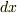 とすると(1)が成り立ちます.
このとき
とすると(1)が成り立ちます.
このとき  はばねの微小部分
はばねの微小部分 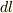 にはたらく力ですが,これは下端から自然長で
にはたらく力ですが,これは下端から自然長で 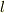 までの部分にはたらく重力に等しく,
までの部分にはたらく重力に等しく, 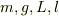 を用いて表すことができます.
これからばね全体の伸び
を用いて表すことができます.
これからばね全体の伸び  が
が
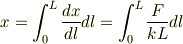
で求められます.
Re: 自重でのばね振り子の周期
toorisugari no Hiro さんのレス (2008/06/11(Wed) 16:17)
あれ? 1/2のfactorがでないですが.... (大雑把にいってばねの重心(L/2)に荷重があるわけですよね.)
Re: 自重でのばね振り子の周期
yama さんのレス (2008/06/11(Wed) 16:26)
が
に比例するので積分すれば1/2のfactorが出ると思います.
Re: 自重でのばね振り子の周期
DIO さんのレス (2008/06/12(Thu) 10:52)
質問者ではないのですが失礼します 解いてみたのですが,よく分からないことがありまして,,
バネを自然長においてn等分した部分のつり合いの式を考えると,
ある部分のバネ定数,バネの伸びをそれぞれ 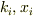 として(
として( 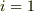 がバネの下端)
がバネの下端)
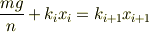
これより
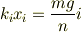
また, 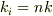 なので
なので
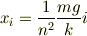
よって
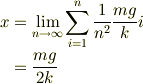
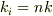 というのが勘でしたが答えがyamaさんの出されたものと同じみたなのであってそうな気がしてます.
というのが勘でしたが答えがyamaさんの出されたものと同じみたなのであってそうな気がしてます.
自分で書いておいてなんですが何故 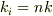 が成り立つんでしょうか
が成り立つんでしょうか
Re: 自重でのばね振り子の周期
yama さんのレス (2008/06/12(Thu) 13:28)
ばねを水平に引く場合のように,ばね全体に一様な力  が加わる場合を考えます.
このとき,ばね全体について
が加わる場合を考えます.
このとき,ばね全体について 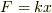 ,n等分した各部分について
,n等分した各部分について 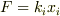 が成り立ちます.
また,各部分の伸びは等しく,その和がばね全体の伸びに等しいので
が成り立ちます.
また,各部分の伸びは等しく,その和がばね全体の伸びに等しいので 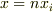 の関係があります.
これらの関係式から
の関係があります.
これらの関係式から 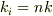 が導かれます.
が導かれます.
Re: 自重でのばね振り子の周期
DIO さんのレス (2008/06/12(Thu) 23:26)
なるほど,結局yamaさんがNo.20271のはじめの方で書かれていたことと同じ分けですね. 有り難うございました.
力が一様で無くても 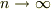 とすることでこれが成り立つ,という理解であってますでしょうか
とすることでこれが成り立つ,という理解であってますでしょうか