時間発展するときの，井戸型ポテンシャル

メントスさんの書込 (2008/06/08(Sun) 17:12)

連続で申し訳ありませんが，またよろしくお願いします．(たぶん，これからかなりの頻度でお世話になると思いますが・・・．)

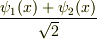屈折率nの一様な媒質中に閉じ込められた一個の電子の運動を考える．この電子は無限に高いポテンシャル障壁に囲まれた長さLのx軸上の線分OAの上を自由に運動できるものとする． 1番は，固有関数と固有エネルギーを求めよ，というものです． 2,時刻 t=0 に電子が $\frac{\psi_{1}(x)+\psi_{2}(x)}{\sqrt{2}}$ という状態にあったとする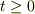． $t\ge 0$ において，線分の片側半分 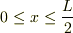$0\le x\le \frac{L}{2}$ に電子がある存在確率を求め，電子がどのように振舞うのか述べよ．

今まで定常状態のポテンシャル問題しか解いたことがなく，そこからさらに時間発展するタイプの問題は初めてですので，あまり自信がありません．添削をお願いできますか？

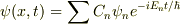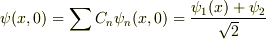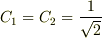
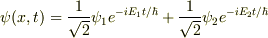自分の解答，波動関数を $\psi(x,t)=\sum C_{n}\psi_{n}e^{-iE_{n}t/\hbar}$ と展開．初期条件から， $\psi(x,0)=\sum C_{n}\psi_{n}(x,0)=\frac{\psi_{1}(x)+\psi_{2}}{\sqrt{2}}$ よって， $C_{1}=C_{2}=\frac{1}{\sqrt{2}}$ $\psi(x,t)=\frac{1}{\sqrt{2}}\psi_{1}e^{-iE_{1}t/\hbar}+\frac{1}{\sqrt{2}}\psi_{2}e^{-iE_{2}t/\hbar}$ 定常状態の波動関数は規格化してあります．存在確率は $|\psi(x,t)|^{2}=\psi^{*}(x,t)\psi(x,t)=\frac{1}{L}[sin^{2}(\frac{\pi}{L}x)-2e^{i(E_{2}-E_{1}/\hbar)t}sin(\frac{\pi}{L}x)sin(\frac{2\pi}{L}x)+sin^{2}(\frac{2\pi}{L}x)]$ 一項目，三項目に2倍角の公式，二項目に和積の公式を使って $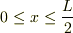0\le x\le \frac{L}{2}$ で積分すると $\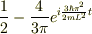frac{1}{2}-\frac{4}{3\pi}e^{i\frac{3\hbar \pi^{2}}{2mL^{2}}t}$ となりました． $\psi_{2}$ 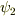の寄与の分から，電子の振る舞いとしては，存在確率は二分の一から振動的に増加，減少する．励起状態の寄与のため，時間的に振動するのは，直観的には正しいような感じがします．よろしくおねがいします．

Re: 時間発展するときの，井戸型ポテンシャル

yama さんのレス (2008/06/08(Sun) 21:21)

考え方としては良いと思いますが，存在確率が複素数になるのはおかしくはないでしょうか？計算をチェックしてみてください．

Re: 時間発展するときの，井戸型ポテンシャル

メントスさんのレス (2008/06/09(Mon) 02:02)

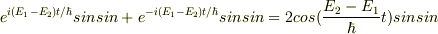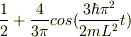そのとおりでした．複素数はあり得ないですね．答えを出した後の，物理的な考察がぜんぜん出来ていませんでした． sinsinに付いてるeは異符号であることを見落としていましたので，正しくは $e^{i(E_{1}-E_{2})t/\hbar}sinsin+e^{-i(E_{1}-E_{2})t/\hbar}sinsin=2cos(\frac{E_{2}-E_{1}}{\hbar}t)sinsin$ で，答えは $\frac{1}{2}+\frac{4}{3\pi}cos(\frac{3\hbar \pi^{2}}{2mL^{2}}t)$ 結果は同じく，二分の一から振動的に変化します．

Re: 時間発展するときの，井戸型ポテンシャル

星野さんのレス (2008/06/09(Mon) 07:21)

これはアメリカのゲームです．１度やってみてください．これは，たった３分でできるゲームです．試してみてください．驚く結果をご覧いただけます．このゲームを考えた本人は，メールを読んでからたった１０分で願い事がかなったそうです．このゲームは，おもしろく，かつ，あっと驚く結果を貴方にもたらすでしょう．約束してください．絶対に先を読まず，１行ずつ進む事．たった３分ですから，ためす価値ありです．まず，ペンと，紙をご用意下さい．先を読むと，願い事が叶わなくなります． ?まず，１番から，１１番まで，縦に数字を書いてください． ?１番と２番の横に好きな３〜７の数字をそれぞれお書き下さい． ?３番と７番の横に知っている人の名前をお書き下さい．（必ず，興味のある性別名前を書く事．男なら女の人，女なら男の人，ゲイなら同姓の名前をかく）必ず，１行ずつ進んでください．先を読むと，なにもかもなくなります． ?４，５，６番の横それぞれに，自分の知っている人の名前をお書き下さい．これは，家族の人でも知り合いや，友人，誰でも結構です．まだ，先を見てはいけませんよ！！ ?８，９，１０，１１番の横に，歌のタイトルをお書き下さい． ?最後にお願い事をして下さい．さて，ゲームの解説です．

１）このゲームの事を，２番に書いた数字の人に伝えて下さい．２）３番に書いた人は貴方の愛する人です．３）７番に書いた人は，好きだけれど叶わぬ恋の相手です．４）４番に書いた人は，貴方がとても大切に思う人です．５）５番に書いた人は，貴方の事をとても良く理解してくれる相手です．６）６番に書いた人は，貴方に幸運をもたらしてくれる人です．７）８番に書いた歌は，３番に書いた人を表す歌．８）９番に書いた歌は，７番に書いた人を表す歌．９）１０番に書いた歌は，貴方の心の中を表す歌．１０）そして，１１番に書いた歌は，貴方の人生を表す歌です．この書き込みを読んでから，１時間以内に１０個の掲示板にこの書き込みをコピーして貼って下さい．そうすれば，あなたの願い事は叶うでしょう．もし，貼らなければ，願い事を逆のことが起こるでしょう．とても奇妙ですが当たってませんか？

[home] [掲示板] [ページの先頭]