振動子の問題です

えりさんの書込 (2008/06/07(Sat) 20:46)

以下の問題を解いてみたのですが，これでよいのか添削していただけないでしょうか？

「二本の，ばね定数それぞれkのばねが直列につながれている．左から数えて一本目の左端は壁に固定されており，一本目のばねの右端と二本目の左端の間と二本目の右端には質量mのおもりがそれぞれ一つずつつながれている．最右端を静かに引き，ゆっくり離すとおもりの運動はどのようになるか．ただし，床との摩擦はないものとし，空気抵抗も無視できるものとする．」

という問題なのですが，これをラグランジアンを用いて解いてみました．おもりの静止位置からの変位を左のおもりから 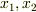$x{_1},x{_2}$ としたとき，ラグランジアンは 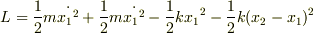$L=\frac{1}{2}m\dot{x{_1}{^2}}+\frac{1}{2}m\dot{x{_1}{^2}}-\frac{1}{2}kx{_1}{^2}-\frac{1}{2}k(x{_2}-x{_1}){^2}$ でよいのでしょうか？