ポテンシャル 2次元
ポテンシャル 2次元
たけ さんの書込 (2008/06/02(Mon) 23:34)
はじめまして.
大学1年のたけというものです.
少しわからないことがあって書き込みました.
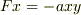 ,
, 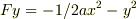 のポテンシャルエネルギー(x=y=0のとき0)を求める問題です.
のポテンシャルエネルギー(x=y=0のとき0)を求める問題です.
少し混乱しているのですが,この問題はxで積分するのと,yで積分するのでは答えが違ってきます.ただ,Fx=-dU/dxのことを考えると,yで積分した
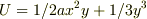 が正しいような気がします・・・
頭が混乱していてすみません・・・
何かアドバイスを頂けたらいいなと思います
が正しいような気がします・・・
頭が混乱していてすみません・・・
何かアドバイスを頂けたらいいなと思います
Re: ポテンシャル 2次元
yama さんのレス (2008/06/02(Mon) 23:46)
まず,ポテンシャルが存在する条件 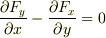 が満たされていることを確認しましょう.
ポテンシャルが存在するならば
が満たされていることを確認しましょう.
ポテンシャルが存在するならば
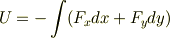
で求められます. 積分経路は(0,0)から(x,y)までの任意の経路ですが,計算が簡単になるように,たとえば(0,0)→(x,0)→(x,y)の経路を選べばよいでしょう. (0,0)→(x,0)の積分が0になるので,たけさんの計算で合っているようですね. また,これ以外の任意の積分経路についても積分値が同じになることを確認しておくとよいでしょう.
Re: ポテンシャル 2次元
たけ さんのレス (2008/06/03(Tue) 00:13)
すばやい返信ありがとうございます.
yamaさんの解法で解くと,
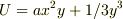 となってしまい,
となってしまい, 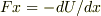 とならないのですが,計算の仕方が違うのでしょうか?
わからないことだらけですみません・・・
とならないのですが,計算の仕方が違うのでしょうか?
わからないことだらけですみません・・・
Re: ポテンシャル 2次元
yama さんのレス (2008/06/03(Tue) 00:36)
まず(0,0)→(x,0)の積分を考えます.
このとき,  なので積分は0になります.
なので積分は0になります.
次に(x,0)→(x,y)を考えると
xを一定に保つので 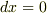 となり,xについての積分は0です.
従ってyについての積分だけを計算すれば,たけさんの初めの計算のようになります.
となり,xについての積分は0です.
従ってyについての積分だけを計算すれば,たけさんの初めの計算のようになります.