相対論　時空比普遍の定理結論

フジモリさんの書込 (2008/06/01(Sun) 13:25)

いろいろな点を指摘されましたが本質は，確定解のある連立方程式を変形しても解以外の有意な情報を引き出すことはできない，ということに帰結するようです．最初からその点に気付くべきでした．いろいろお教え頂いて有難うございました．方程式(1a)(1b)と(2a)(2b)を連立したことが原因でしょうか．空間の等方性から何らかの時空の縛りがでてくる筈だと睨んだのですが．x2*t1=x1*t2 が解として導かれる方程式がもしあれば，未知数>方程式数の条件でしょう．アイデアが浮かびましたが(下手な考え)夏休みにでも考えをまとめてみます．

Re: 相対論　時空比普遍の定理結論

yama さんのレス (2008/06/02(Mon) 22:58)

空間の等方性からは，γ(v)=γ(-v) の関係があることが言えますが，それだけでは有限の不変速度の存在は出てきません．このことは，ガリレイ変換の場合でも空間が等方的であることを考えれば明らかです．

また，フジモリさんが書かれた(1a)(1b)は，任意の座標(x1,t1)について成り立つ座標変換の式であり，光速度不変の原理またはそれに代わる何らかの条件によってγ(v)を定めればローレンツ変換の式になります．しかし，ローレンツ変換の式を用いても，(x1,t1)を任意の座標とする限り t2*x1=t1*x2 は導けません．特別な場合として t1=0 に原点から出た光の経路を(x1,t1)とするときは，x1=c*t1 の関係があるので，t2*x1=t1*x2 が成り立ちます．しかし，そのような特別の場合を除けば一般には t2*x1=t1*x2 は成り立ちません．つまり(x1,t1)について（光の経路であるなど）何らかの条件を課さない限り，座標変換の式だけから t2*x1=t1*x2 の関係を導くことはできないということです．

Re: 相対論　時空比普遍の定理結論

フジモリさんのレス (2008/06/09(Mon) 22:14)

yamaさん，丁寧な対応痛み入ります．結局今回の誤りは不用意に(1a)(1b)と(2a)(2b)を連立の仲間に入れたことでした．

>つまり(x1,t1)について（光の経路であるなど）何らかの条件を課さない限り，座標変換の式だけから t2*x1=t1*x2 の関係を導くことはできないということです． →相対性原理の満たすべき相対性/対称性とは何かという問題に帰着します．逆転の発想です．S2,S3で物理法則が同じになるためには，(3a)(3b)の対称性より連立させる要があります．

頻繁な掲示板でのやりとりは邪魔のようですので，できればメールをいただけませんか．

Re: 相対論　時空比普遍の定理結論

yama さんのレス (2008/06/10(Tue) 00:17)

フジモリさんは，時空比普遍の定理自体自体は正しいのに，証明に不備があるので他の人の理解が得られないのだというお考えのようですね．もちろん証明は間違いだらけですが，その証明を修正すれば定理が成り立つわけではありません．定理自体が間違っているのです．

なぜなら(x1,t1)に何の条件もついていないのに相対性原理や空間の対称性によってt2*x1=t1*x2 が成り立つことはないからです．そもそも相対性原理や空間の対称性はガリレイ変換の場合にも成り立つので，フジモリさんの考え方に従えばガリレイ変換でも時空比普遍の定理が成り立つことになります．

また，S2,S3で物理法則が同じになるために(3a)(3bが成り立つ必要もありません．

間違っている定理を証明しようとするのは全く無駄なことであり，無駄なことについてこれ以上の議論はあまりしたくありません．掲示板では，間違った記事を放置すると黙認していると受け取られる虞があるので，やむを得ず返信していますが，メールのやりとりは遠慮しておきます．

一筆言上

フジモリさんのレス (2008/06/29(Sun) 10:20)

yamaさん，飯でも一緒に食いませんか． >空間の等方性からは，γ(v)=γ(-v) の関係があることが言えますが，それだけでは有限の不変速度の存在は出てきません．このことは，ガリレイ変換の場合でも空間が等方的であることを考えれば明らかです． >そもそも相対性原理や空間の対称性はガリレイ変換の場合にも成り立つので，フジモリさんの考え方に従えばガリレイ変換でも時空比普遍の定理が成り立つことになります

ガリレイ変換はv=0で成り立つ論理．v≠0のとき，γ(v)即ちγ(v)^2の対称性が核心の小生の論理を否定する根拠にはなりません．No20003の式(6)を再掲しておきます． γ(v)^2=c2*c1/{(c1-v)(c2+v)}=c1*c2/{c1*c2+(c1-c2)v-v*v}(6) γ(v)^2がvの偶関数となるためにはvの一次係数は0となる必要があります．これだれで有限の不変速度の存在は出てきます．

Re: 一筆言上

yama さんのレス (2008/06/29(Sun) 17:10)

ガリレイ変換はv≠0でも成り立ち，γ(v)=γ(-v)=1 です．従って当然vの一次係数は0となります．

そのため，フジモリさんの論法ではガリレイ変換の場合も(6)が成り立つことになります．しかし，実際にはガリレイ変換の場合に(6)は成り立ちません．それは，フジモリさんの論法が間違っているということです．

Re: 一筆言上

フジモリさんのレス (2008/07/18(Fri) 08:11)

ガリレイ変換の前提は光速の瞬達です．(6)は γ(v)^2=c2*c1/{(c1-v)(c2+v)}=1/{1-v/c1)(1+v/c2)} と変形されるので同じ前提(c1=∞,c2=∞)に立てば，v≠0でもγ(v)^2=γ(-v)^2=1 となるが，これを前提が異なる議論，即ち有限速度(c1≠∞,c2≠∞)を前提とする議論に適用しても無意味でしょう．

Re: 一筆言上

yama さんのレス (2008/07/18(Fri) 09:10)

そもそもc1=x1/t1,c2=x2/t2が光速度であるという前提はありません．従って，ガリレイ変換ではc1=∞,c2=∞を前提にしているわけではありません

数式で語れば

フジモリさんのレス (2008/07/31(Thu) 09:24)

x2=γ(v)(x1-v*t1) (1a) x1=γ(v)(x2+v*t2) (1b) γ(v)が決まれば座標変換が確定する．連立方程式(1a)(1b)にγ(v)=γ(-v)の条件を適用する． (イ) (1a)+(1b)より γ(v)=(x1+x2)/{x1+x2-v(t1-t2)}(3) t1=t2[=t] のときγ(v)=γ(-v)=1 となり，ガリレイ変換 x2=x1-v*t を得る． (ロ) t1≠t2 のとき，(1a)*(1b)より x2*x1=γ(v)^2(x1-v*t1)(x2+v*t2) γ(v)^2=x2*x1/{(x1-v*t1)(x2+v*t2)}(4) ここで，x1/t1=c1,x2/t2=c2 と置いて γ(v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2}(6) c1=c2 [=C] のとき γ(v)^2=C^2/(C^2-v^2) となり，変換が定まる．

(ハ)γ(v)は他にも求まるが，無意味なため無視．これは対称性の崩れによるものと考えられる．

(イ)と(ロ)は別ケースとして扱う必要がある．

Re: 数式で語れば

yama さんのレス (2008/07/31(Thu) 10:37)

(1a)と(1b)が成り立てば，c1≠c2 であっても γ(v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2} は成り立ちます．これは導き方から明らかです．そもそも c1-c2 はvの関数なので，これを定係数として扱うことはできません．

Re: 数式で語れば

フジモリさんのレス (2008/08/27(Wed) 14:47)

yamaさん，今迄のガリレイ変換を根拠にした否定論は取り下げられるのですか．

>(1a)と(1b)が成り立てば，c1≠c2 であっても γ(v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2} は成り立ちます．

ここでγ(v)^2=γ(-v)^2 の条件を適用してみて下さい．

>そもそも c1-c2 はvの関数なので，

根拠はなんですか．

Re: 数式で語れば

yama さんのレス (2008/08/29(Fri) 21:30)

>今迄のガリレイ変換を根拠にした否定論は取り下げられるのですか．

取り下げません．今までの議論と今回の議論は別のものです．

>ここでγ(v)^2=γ(-v)^2 の条件を適用してみて下さい．

γ(-v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2} になるだけです．あるいは，すべてのvを-vで置き換えるということなら，c1-c2に含まれるv（下記の式の中のv）も-vで置き換えないといけません．

>根拠はなんですか．

(1a)と(1b)を用いるとx2,t2をx1,t1で表すことができ，次の結果が得られます．

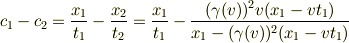
$c_1-c_2=\frac{x_1}{t_1}-\frac{x_2}{t_2}=\frac{x_1}{t_1}-\frac{(\gamma(v))^2v(x_1-vt_1)}{x_1-(\gamma(v))^2(x_1-vt_1)}$

これは一般にはvの関数です．

Re: 数式で語れば

フジモリさんのレス (2008/10/15(Wed) 12:36)

>γ(-v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2} になるだけです．

γ(v)^2=γ(-v)^2 の条件はv→-vとしても原式は不変ということだから，c1=c2 となります．

>あるいは，すべてのvを-vで置き換えるということなら，c1-c2に含まれるv（下記の式の中のv）も-vで置き換えないといけません．

(1a)と(1b)から導いた式γ(-v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2} に，(1a)と(1b)から導いたvを含む式 (c1-c2) を置き換えても恒等式が得られるだけで無意味です．

Re: 数式で語れば

yama さんのレス (2008/10/15(Wed) 14:22)

>γ(v)^2=γ(-v)^2 の条件はv→-vとしても原式は不変ということだから，c1=c2 となります．

c1，c2 のどちらかはｖの関数であってv→-vの置き換えをすれば，c1またはc2が変化します．つまり，c1-c2 はvに無関係な係数ではないので，これを0と置くことはできません．

>(1a)と(1b)から導いた式γ(-v)^2=c1*c2/{c1*c2+(c1-c2)v-v^2} に，(1a)と(1b)から導いたvを含む式 (c1-c2) を置き換えても恒等式が得られるだけで無意味です．

良いところに気付かれましたね．まさにその通りであって，恒等式が得られるだけです．ということは x1/t1=x2/t2（すなわちc1=c2）を導くことはできないわけです．フジモリさんは，x1/t1=c1，x2/t2=c2 と置き換えて，c1-c2 をあたかも係数であるかのように扱って c1=c2 を導かれたわけですが，置き換えをもとに戻せば恒等式になるのですから，全く無意味なことをされていたわけです．