ボース凝縮
ボース凝縮
メントス さんの書込 (2008/05/31(Sat) 14:27)
質量mの粒子がN個ある体積Vの理想気体がマクスウェル分布に従うとする. 不確定性関係を利用して,おおよその波束の広がり?xを求め,その結果を利用してボースアインシュタイン凝縮を起こす温度を求めよ という問題なのですが, まず,マクスウェルボルツマン分布を使って,?p=√(<p^2>-<p>^2)はもとまりました.√{mkT(3-(8/π))}になりました. そのつぎに,?x?p=hから,?xも求まりましたが,そこからどうやって温度を求めるのかが分かりません.転移温度はT=(h^2/2πmk)(N/ξV)^(2/3)だと思います. つまり,NとVに依存するわけですが,その2つはすでに問題文に与えられているので,?xを使う必要がないのではないのか?と思うのですが・・・.
Re: ボース凝縮
メントス さんのレス (2008/06/02(Mon) 19:19)
こちらの掲示板は,同時に複数の質問をしてもよろしいのでしょうか? 大学院試験の勉強をしていて,お尋ねしたいことが結構あるんです. 迷惑になるのなら控えます.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/02(Mon) 19:47)
複数の質問は別スレッドに分けた方が答える方に楽です. # 一つずつ質問される方がbetterです.
後,メントスさんが既にされたご質問は文字化けがある以外にも,情報が足りないので,誰も答えられないのだと思います.
Re: ボース凝縮
メントス さんのレス (2008/06/03(Tue) 16:12)
わかりました.なるべく一つの疑問が解決してから,新しい記事を立てますが もしかしたら,2つの記事を立てることもあるかもしれません.どうぞ,よろしくおねがいします.
私の環境からは文字化けしていないので,気付きませんでした.
何がいけなかったのでしょうか?不慣れですが,teXを使ってみます.
もう一度問題を書きます
質量がmのN個の粒子からなる体積Vの理想気体を考える.ボルツマン定数をkとする.
1,この系が絶対温度Tのマクスウェルボルツマン分布に従うとして運動量の標準偏差を求めよ.
で,自分の解答が
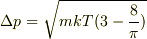 2,この結果を利用して,各粒子の量子力学的な波束のおおよその空間的な広がりを求めよ.
不確定性原理
2,この結果を利用して,各粒子の量子力学的な波束のおおよその空間的な広がりを求めよ.
不確定性原理 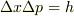 から
から
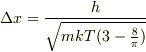 3,この結果を利用して,系が理想ボース気体である場合にボースアインシュタイン凝縮を起こす温度を求めよ.
温度は
3,この結果を利用して,系が理想ボース気体である場合にボースアインシュタイン凝縮を起こす温度を求めよ.
温度は 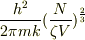 というのは知っています.
ボース凝縮を起こす温度は粒子密度N/Vに依存していて,今,NとVはどちらも
問題から与えられているので,これで上の式が答えでいいと思うのですが
2の結果を利用して,というのはどういうことなのでしょうか?
温度の表式のどこに
というのは知っています.
ボース凝縮を起こす温度は粒子密度N/Vに依存していて,今,NとVはどちらも
問題から与えられているので,これで上の式が答えでいいと思うのですが
2の結果を利用して,というのはどういうことなのでしょうか?
温度の表式のどこに 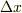 を使うのかが分かりません.
を使うのかが分かりません.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/03(Tue) 16:52)
(問題は上で書かれた物で完全なのですね?) えっと,この手の問題は苦手なので識者が来てくれるまでの場つなぎ.
(1)
> で,自分の解答が
> 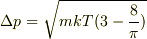
なんか係数が変ですね.導出を書いてもらえませんか?
(3) 公式を近似的に導き出せという問題では? 何らかのモデルを立てて,それから計算してみる. たとえば(根拠の説明を要求されると困るが), 「波束の拡がりが粒子間隔より大きくなるときボース凝縮を起こす」 とか.
Re: ボース凝縮
serge さんのレス (2008/06/03(Tue) 18:24)
量子力学では,粒子的な振る舞いを考える時,波束を作って考えます.
そのため,波束の広がり=粒子の直径とみなせます.
このとき体積  の系には
の系には 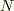 個の粒子があるので
通常,(粒子の全体積)
個の粒子があるので
通常,(粒子の全体積) 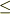
 でなければならないから
でなければならないから
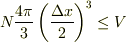 となります.
よって
となります.
よって 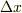 はメントスさんのを用いると
はメントスさんのを用いると
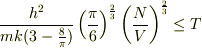 となります.
すなわち
となります.
すなわち 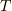 がこの温度より小さい時ボーズアインシュタイン凝縮をすることがいえます.
がこの温度より小さい時ボーズアインシュタイン凝縮をすることがいえます.
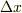 はあってるのかなぁ・・・(確認していないけれども)
はあってるのかなぁ・・・(確認していないけれども)
Re: ボース凝縮
メントス さんのレス (2008/06/03(Tue) 19:20)
なぜみなさんそんなに数式を打つのが早いのですかw 何か特別なソフトでも使っていらっしゃるのでしょうか?手打ちですよね?
運動量の標準偏差の導出を書きます.
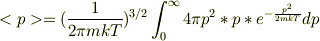
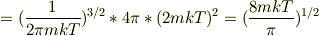
また,
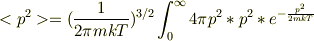
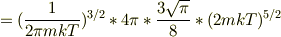
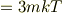
よってゆらぎは,
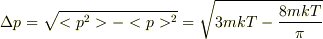 です.
toorisugari no Hiroさんもsergeさんも,おっしゃられていることは同じで
公式を使うのではなく,自分で導出することを問題は求めているということですね?
私も,問題の意図がそういうことなのかな?と考えていましたが
です.
toorisugari no Hiroさんもsergeさんも,おっしゃられていることは同じで
公式を使うのではなく,自分で導出することを問題は求めているということですね?
私も,問題の意図がそういうことなのかな?と考えていましたが
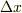 の条件が分かりませんでした.sergeさんのおっしゃられた条件は,統計力学の本なら必ず載っているような有名なものだったのでしょうか?ボース凝縮は一度習ったのですが,知りませんでした・・・.
その条件の意味に関しては,もう少しよく考えてみるのでちょっと待ってください.
問題はまだ,4,5とあって,まだ手をつけていないので詳しくは分からないのですが
4,1粒子エネルギーは量子化されているが,粒子系はマクスウェルボルツマン分布に従うときに,Nと同程度の数の粒子が最低エネルギー状態を占め始める温度を求めよ.ただし,1粒子エネルギーは系が体積Vに閉じ込められている場合のエネルギー.
5,粒子数密度を一定にしつつ,粒子数と体積を無限大にする極限での比(3のT/4のT)を求め,なぜそうなるのか理由を述べよ.
の条件が分かりませんでした.sergeさんのおっしゃられた条件は,統計力学の本なら必ず載っているような有名なものだったのでしょうか?ボース凝縮は一度習ったのですが,知りませんでした・・・.
その条件の意味に関しては,もう少しよく考えてみるのでちょっと待ってください.
問題はまだ,4,5とあって,まだ手をつけていないので詳しくは分からないのですが
4,1粒子エネルギーは量子化されているが,粒子系はマクスウェルボルツマン分布に従うときに,Nと同程度の数の粒子が最低エネルギー状態を占め始める温度を求めよ.ただし,1粒子エネルギーは系が体積Vに閉じ込められている場合のエネルギー.
5,粒子数密度を一定にしつつ,粒子数と体積を無限大にする極限での比(3のT/4のT)を求め,なぜそうなるのか理由を述べよ.
というものなのですが,もしかして4が公式のTで,それと3で立てたモデルから計算したTとを比べなさいって問題なのでしょうか.
Re: ボース凝縮
serge さんのレス (2008/06/03(Tue) 21:39)
>>が公式のTで,それと3で立てたモデルから計算したTとを比べなさいって問題なのでしょうか
ボーズアインシュタイン凝縮の物理的意味を聞いているのだと思います. どの本にも「ボーズアインシュタイン凝縮とは〜という現象〜」てな感じのことが書いてあると思います.要はそれを考えさせる問題だと思います.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/03(Tue) 22:15)
メントスさんの計算した 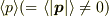 は意味不明です.
そもそも運動量はベクトルですから
は意味不明です.
そもそも運動量はベクトルですから
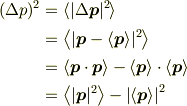
で計算しなければいけないのでは?
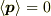 ですから
ですから 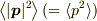 だけでいいのです.
だけでいいのです.
Re: ボース凝縮
serge さんのレス (2008/06/04(Wed) 13:39)
ですから,今対称性より
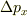 を求めればよいと思います.
そうすると,「波束の広がり=粒子の大きさ」というイメージがわきやすいのでは?
を求めればよいと思います.
そうすると,「波束の広がり=粒子の大きさ」というイメージがわきやすいのでは?
あと,自信が無いのですが,今の場合
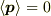 では気体の圧力が0になってしまうはずだと思いますが
では気体の圧力が0になってしまうはずだと思いますが
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 13:51)
> あと,自信が無いのですが,今の場合
> 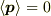 では気体の圧力が0になってしまうはずだと思いますが
では気体の圧力が0になってしまうはずだと思いますが
単に重心系で見てるだけの話(平均速度=0)で,圧力(運動量揺らぎの2乗相当)とは関係ありません.
Re: ボース凝縮
メントス さんのレス (2008/06/04(Wed) 14:06)
まだボース凝縮について考え中なのですが,レスがついていたので,運動量に関してだけ.
今は運動量の大きさのみを考えれば良いのではないのですか?
運動量は今の場合,等方的であると考えて,マクスウェルボルツマン分布の積分を 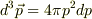 としました.
toorisugari no Hiroさんの指摘はもっともなのですが,速さの揺らぎを計算する似たような問題で,同じように計算していたので・・・.
波束について考えてる今の場合,運動量の大きさ平均は
としました.
toorisugari no Hiroさんの指摘はもっともなのですが,速さの揺らぎを計算する似たような問題で,同じように計算していたので・・・.
波束について考えてる今の場合,運動量の大きさ平均は 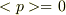 にはならないのではないのでしょうか?
にはならないのではないのでしょうか?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 14:14)
単原子分子気体の運動エネルギーは3方向でのエネルギー等分配則により
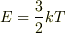
運動エネルギーの式
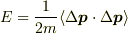
メントスさんの考え方でこれらの間に整合性がありますか?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 14:16)
> 波束について考えてる今の場合,運動量の大きさ平均は 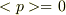 にはならないのではないのでしょうか?
にはならないのではないのでしょうか?
静止した波束で何か問題がありますか?
Re: ボース凝縮
メントス さんのレス (2008/06/04(Wed) 14:48)
>toorisugari no Hiroさん 1粒子のエネルギーの表式は
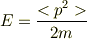
ではないでしょうか? 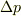 はあくまで揺らぎなので,エネルギーの式とは関係ないように思います.
はあくまで揺らぎなので,エネルギーの式とは関係ないように思います.
>yamaさん
問題文には,運動量の大きさ,とは具体的に書いてはありませんが
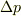
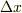 を求めよ,と書いてあるので,sergeさんがおっしゃるように
を求めよ,と書いてあるので,sergeさんがおっしゃるように 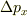 を求めて,
を求めて, 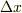 と不確定性原理を使うことを問題は求めているのではないのでしょうか?私は動径方向の運動量を求めてしまいましたが,
と不確定性原理を使うことを問題は求めているのではないのでしょうか?私は動径方向の運動量を求めてしまいましたが, 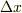 を動径方向の位置と考えれば同じことだと思います.
なので,この問題では,ベクトルではなく,大きさを考えなければならないと思ったのですが・・・.
を動径方向の位置と考えれば同じことだと思います.
なので,この問題では,ベクトルではなく,大きさを考えなければならないと思ったのですが・・・.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 14:59)
> 1粒子のエネルギーの表式は
> 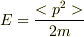 > ではないでしょうか?
> ではないでしょうか?
とすると,この系に対して 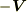 で動いている系から見ると
で動いている系から見ると 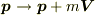 ,
これと
,
これと
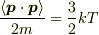 より,
より,
(ニュートン力学の範囲内で) 「動いている系で観測した温度は止まっている系で観測した温度と違う」
という結果になってしまいます.
この手の量はガリレイ不変に作らないとダメです.
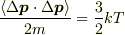 なら系によりません.
なら系によりません.
Re: ボース凝縮
メントス さんのレス (2008/06/04(Wed) 15:25)
そこまで深く考えてはいなかったのですが, マクスウェルボルツマン分布の計算をするときに,自由粒子の運動量が等方的であることを仮定して,計算してきたので,観測系が等速運動しているような状況はまた別に考えなければならないのではないのでしょうか?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 15:37)
> マクスウェルボルツマン分布の計算をするときに,自由粒子の運動量が等方的であることを仮定して,計算してきたので,観測系が等速運動しているような状況はまた別に考えなければならないのではないのでしょうか?
そのときはマクスウェルボルツマン分布がかわります(ピークの位置がずれます).メントスさんが使われたのは,平均速度(or 平均運動量)が0になる系での分布式です.
Re: ボース凝縮
yama さんのレス (2008/06/04(Wed) 16:09)
一旦書き込みましたが,疑問が生じたので前のレスは削除しました.
改めて考えてみると,標準偏差についてはtoorisugari no Hiroさんのように考えることもできますが,本問の場合はsergeさんのやり方が適切であるように思います.
というのは,不確定性関係は正準共役な物理量p,qについての関係なので,各座標とそれに対応する運動量についてなりたちます.
しかし運動量の大きさをpとすると,それに共役な物理量が何になるのかよくわかりません.(運動量の大きさpと極座標での運動量の動径成分 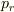 は別のものです.)
デカルト座標の各成分に分けて不確定性関係を考えるのが適切であると思います.
しかし,おおよその温度を求めるのであればtoorisugari no Hiroさんのやり方でもいいように思います.
は別のものです.)
デカルト座標の各成分に分けて不確定性関係を考えるのが適切であると思います.
しかし,おおよその温度を求めるのであればtoorisugari no Hiroさんのやり方でもいいように思います.
また,温度に関係するのは内部エネルギーなので,全体が運動しているときは,全運動エネルギーから,系全体としての並進運動のエネルギーを差し引く必要があります. 従って観測する基準系によって温度が変わることはないと思います.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 16:26)
>また,温度に関係するのは内部エネルギーなので,全体が運動しているときは,全運動エネルギーから,系全体としての並進運動のエネルギーを差し引く必要があります.
つまり,
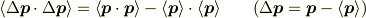
により
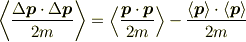
ですね.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 16:39)
> 改めて考えてみると,標準偏差についてはtoorisugari no Hiroさんのように考えることもできますが,本問の場合はsergeさんのやり方が適切であるように思います.
つまり,エネルギー等分配のファクター3が温度の式から消える,というわけですね. 同意します.
Re: ボース凝縮
yama さんのレス (2008/06/04(Wed) 16:41)
どちらもそういうことになると思います.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 19:55)
1方向のマックスウェルボルツマン分布
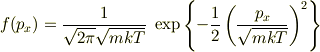
を使えば,
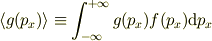
により
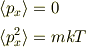
となり,
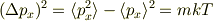
が得られます.ここで,等方性により
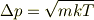
と出ます.
同じ話をメントスさんの論法でなぞるなら,
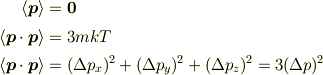
とすべきということですね.(第3式は私も誤解してました.)
あと, 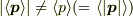 を誤解されていたように思います.
を誤解されていたように思います.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 23:28)
#20151 > 運動量は今の場合,等方的であると考えて,
統計的に等方な運動量分布において,平均として得られる運動量は等方性を持つことになります.しかし,運動量はベクトルです.等方な(回転対称な)ベクトルは 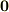 しかありません.これからも
しかありません.これからも 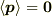 が得られます.
が得られます.
Re: ボース凝縮
メントス さんのレス (2008/06/04(Wed) 23:30)
>toorisugari no Hiroさん
1方向のみの運動量を自分でも計算してみようと思っていたのですが,先にやってくださいましたか.ありがとうございます.
その「誤解されていたように思います」の式は正しいということでいいんですよね?
私は,運動量が等方的であることから,位相空間で極座標を考えて,運動量の大きさ=運動量の動径方向の大きさ(つまり,粒子の運動量が放射線状に方向をもっている)と考えて,運動量の動径方向 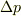 と粒子の動径方向のゆらぎ
と粒子の動径方向のゆらぎ 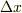 との不確定性関係を考えれば良いと考えていたのですが,答えが違うものになるということは,やはり間違いなのでしょうか.
yamaさんの>運動量の大きさpと極座標での運動量の動径成分は別のものです.
というのがよくわかりません.
との不確定性関係を考えれば良いと考えていたのですが,答えが違うものになるということは,やはり間違いなのでしょうか.
yamaさんの>運動量の大きさpと極座標での運動量の動径成分は別のものです.
というのがよくわかりません.
>sergeさん
ボース凝縮について,もう一度本を読んでみたのですが,教えていただいた条件がよく理解できません.教科書に必ず載っているボース凝縮の条件は
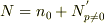 において,基底状態の粒子が存在しないような,ボース凝縮を起こすギリギリのところ
において,基底状態の粒子が存在しないような,ボース凝縮を起こすギリギリのところ 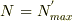 の温度がボース凝縮を起こす温度になると理解したのですが,なぜsergeさんの条件,粒子の全体積
の温度がボース凝縮を起こす温度になると理解したのですが,なぜsergeさんの条件,粒子の全体積 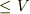 がボース凝縮を起こす条件になるのでしょうか.
粒子の全体積がVより小さいというのは,当たり前というか,別にボース凝縮を起こしていなくても成りなっているような気がするのです.
がボース凝縮を起こす条件になるのでしょうか.
粒子の全体積がVより小さいというのは,当たり前というか,別にボース凝縮を起こしていなくても成りなっているような気がするのです.
Re: ボース凝縮
メントス さんのレス (2008/06/04(Wed) 23:49)
>No.20173
等方的なベクトルの平均が0になるというのは,逆方向のベクトルと互いに打ち消しあって,平均的に0になるということですよね?
私がNo.20134で 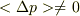 としたのは,出てくる運動量を全てベクトルの大きさのみで考えたからです.積分範囲も0以上にしています.
問題集のマクスウェル速度分布のところに似たような問題が必ず載っているので,私の,その計算自体は合っていると思います.
ただ,今回は
としたのは,出てくる運動量を全てベクトルの大きさのみで考えたからです.積分範囲も0以上にしています.
問題集のマクスウェル速度分布のところに似たような問題が必ず載っているので,私の,その計算自体は合っていると思います.
ただ,今回は 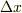 と不確定性関係においてペアになるものを求める,ということで,運動量の大きさを求めたのは間違いで,
と不確定性関係においてペアになるものを求める,ということで,運動量の大きさを求めたのは間違いで, 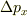 を求めるべきだったと思います.
を求めるべきだったと思います.
PS, toorisugari no Hiroさんの議論はとてもためになることだと思うのですが,正直,成績も並な,ただの学生である私にはちょっとついていけません・・・. 質問に答えてくださる方にたいして失礼かもしれませんが,まずは,この問題を解いてしまいたいと思っています. 一つ一つ解決するまで,少しお待ちいただけませんか?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/04(Wed) 23:51)
> なぜsergeさんの条件,粒子の全体積 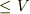 がボース凝縮を起こす条件になるのでしょうか.
がボース凝縮を起こす条件になるのでしょうか.
あくまでも,関連性が曖昧な条件にすぎません. 私やsergeさんの述べた条件は量子気体が古典気体と見なせる条件 「粒子間距離 >>ドブロイ波長」 にすぎないからです.
Re: ボース凝縮
serge さんのレス (2008/06/05(Thu) 00:15)
> なぜsergeさんの条件,粒子の全体積 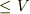 がボース凝縮を起こす条件になるのでしょうか.
がボース凝縮を起こす条件になるのでしょうか.
基本的にtoorisugari no Hiroさんのおっしゃるとおりです. これは,「ボーズ凝縮を起こす条件」ではなくて 古典気体を考えて,それが当然満たすべき条件を出してきただけです. 最後のほうでちょっとだけ量子論を用いると温度に制限がついた結果が導き出されてきたわけで, これはいったい物理的にどういうことなのかと考えると,この問題では「ボーズ凝縮である」といっているわけです (しかもボーズ気体の時とまでことわっています).
普通に考えると,よくて温度が計算で導いた値に近くなると量子力学的効果があらわになってきて古典論の適用限界という結論しか導き出せないと思います.
Re: ボース凝縮
yama さんのレス (2008/06/05(Thu) 00:55)
「極座標での運動量の動径成分」というのは不正確な言い方でした.正確には「極座標の動径  に正準共役な一般化運動量」です.
に正準共役な一般化運動量」です.
極座標では運動エネルギーは
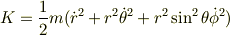
となるので,  に正準共役な運動量は
に正準共役な運動量は
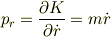
となります.
一方,運動量の大きさを 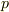 とすると,
とすると, 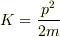 より
より
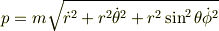
となるので, 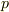 と
と 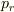 は別のものです.
は別のものです.
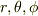 のどれも
のどれも 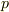 に正準共役な座標でないことは明らかですが,何か別の座標系を考えたとしても,
に正準共役な座標でないことは明らかですが,何か別の座標系を考えたとしても, 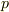 に正準共役な座標というものが存在するかどうかは疑問です.
に正準共役な座標というものが存在するかどうかは疑問です.
運動量の大きさの平均値を求めるだけなら,メントスさんのように,運動量空間の極座標を考えればいいのですが,不確定性関係を考える場合は,通常の空間の座標を考えないといけないので,極座標ではうまくいかないわけです.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 01:13)
No.20153
>> 波束について考えてる今の場合,運動量の大きさ平均は 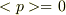 にはならないのではないのでしょうか?
にはならないのではないのでしょうか?
> 静止した波束で何か問題がありますか?
ごめんなさい.「運動量の『大きさ』平均」の『大きさ』を読み落としていました.
確かに 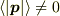 です.でも,これと
です.でも,これと 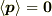 は両立します.
は両立します.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 01:44)
yamaさんが何に悩んでおられるか,わかってきました.難しい問題ですね.
ただ,今までの記事からは,「ベクトル演算子である 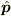 は第二義的で,
は第二義的で, 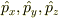 が本質的だ」とおっしゃっているように読めるのですが....
が本質的だ」とおっしゃっているように読めるのですが....
それとも,スカラー演算子 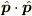 には意味はあるが,演算子
には意味はあるが,演算子 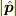 は意味不明(or 第二義的)だ,ということでしたら同意します.
は意味不明(or 第二義的)だ,ということでしたら同意します.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 03:07)
そういえば,3次元での平均 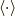 をきちんと定義していませんでしたね.余力があるとき読んでください.
をきちんと定義していませんでしたね.余力があるとき読んでください.
1方向のマックスウェルボルツマン分布
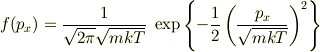
を使って
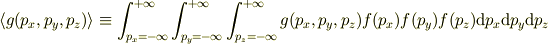
が定義です.
ここで分布関数は
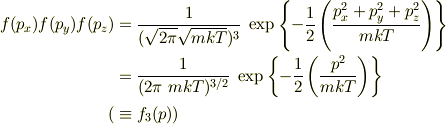
と 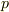 だけの関数になりますが,体積要素の方は極座標表示
だけの関数になりますが,体積要素の方は極座標表示
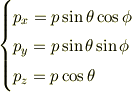
で
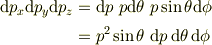
被積分関数も
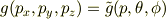
と表され,
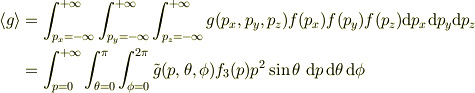
と 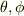 を含んだ表現になります.
もし,
を含んだ表現になります.
もし, 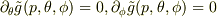 なら,つまり,
なら,つまり,  が
が 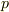 だけの関数なら,
だけの関数なら,
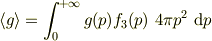
となりますが,一般には 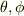 は無視できません.
ですから
は無視できません.
ですから 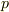 については
については
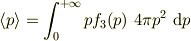
と 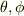 を含まない計算になりますが,
を含まない計算になりますが, 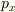 だと
だと
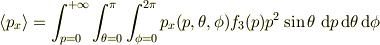
のように 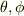 も計算しなければいけません.(元のx,y,zの積分で計算すれば既知の結果,0,になります.)
同じように
も計算しなければいけません.(元のx,y,zの積分で計算すれば既知の結果,0,になります.)
同じように 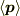 も積分計算をするのですが,そこでは
も積分計算をするのですが,そこでは 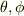 も計算しなければいけません.
も計算しなければいけません.
これが 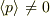 だが,
だが, 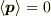 になる傍証です.
になる傍証です.
Re: ボース凝縮
yama さんのレス (2008/06/05(Thu) 10:33)
は正の固有値を持つので,
は(第二義的かもしれませんが)意味を持つと思います.
このとき, ![[\hat q,|\hat{\bm p}|]=i\hbar](http://hooktail.maxwell.jp/bbslog/f4dfae4f7f6e1ecef6955ad6356d7b72.png) となるような演算子
となるような演算子 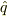 があれば,不確定性関係
があれば,不確定性関係
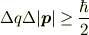
が成り立つのですが,このような演算子があるかどうかが疑問です.
古典論に置き換えれば
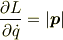
となるような一般化座標  があるだろうかということです.
があるだろうかということです.
Re: ボース凝縮
メントス さんのレス (2008/06/05(Thu) 11:14)
直接ボース凝縮になる条件ではなくて,必要条件ということは理解しました.
>私やsergeさんの述べた条件は量子気体が古典気体と見なせる条件
>「粒子間距離 >>ドブロイ波長」
量子気体が古典気体にみなせる条件は,ドブロイ波長を  とすると
とすると 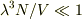 では無かったでしょうか?
toorisugari no Hiroさんのおっしゃってる条件を数式化すると,上の式になりますよね.
ん?量子気体を古典気体にみなす条件がいま必要なのですか?
ちょっと混乱してきました.ボース凝縮になる条件を課すなら,むしろ,逆に古典気体を量子気体とみなせる状況でないといけないのでは?
それと,
では無かったでしょうか?
toorisugari no Hiroさんのおっしゃってる条件を数式化すると,上の式になりますよね.
ん?量子気体を古典気体にみなす条件がいま必要なのですか?
ちょっと混乱してきました.ボース凝縮になる条件を課すなら,むしろ,逆に古典気体を量子気体とみなせる状況でないといけないのでは?
それと, 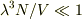 の
の 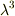 の部分がsergeさんが最初に言っておられた粒子の体積ってことだと思うんですけど,sergeさんの条件は,
の部分がsergeさんが最初に言っておられた粒子の体積ってことだと思うんですけど,sergeさんの条件は, 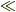 ではなくて,
ではなくて, 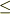 であることも理解できません.
であることも理解できません. 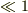 で項が無視できるから,量子気体が古典気体に近似できるので,
で項が無視できるから,量子気体が古典気体に近似できるので, 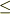 だと,どんな気体でも満たしているのではないのでしょうか.
だと,どんな気体でも満たしているのではないのでしょうか.
>yamaさん 運動量の大きさで考えてしまうと,不確定性関係の共役な関係が良く分からないということ,理解しました. ここからはそれとは関係なく,自分の勘違いの確認なんですけど 自分が「運動量の大きさ」といっていたのはあくまで「位相空間」での動径成分のことで,運動量の動径成分は「実空間」での動径成分であるから,別物.ということでいいんですよね? 位相空間と実空間をごちゃまぜにして考えてしまっていました.
Re: ボース凝縮
yama さんのレス (2008/06/05(Thu) 11:40)
>自分が「運動量の大きさ」といっていたのはあくまで「位相空間」での動径成分のことで,運動量の動径成分は「実空間」での動径成分であるから,別物.ということでいいんですよね?
「位相空間」ではなくて「運動量空間」(運動量 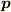 を座標とする空間)での動径成分が運動量の大きさです.
もちろん「実空間」での運動量の動径成分とは別物です.
を座標とする空間)での動径成分が運動量の大きさです.
もちろん「実空間」での運動量の動径成分とは別物です.
「位相空間」は 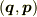 を座標とする空間です.
を座標とする空間です.
Re: ボース凝縮
メントス さんのレス (2008/06/05(Thu) 11:44)
ありがとうございます. 基本的なところで勘違いをしていました.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 13:21)
>「粒子間距離 >>ドブロイ波長」
> 量子気体が古典気体にみなせる条件は,ドブロイ波長を  とすると
とすると 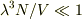 では無かったでしょうか?
では無かったでしょうか?
同じです.気体の「粒子間距離」ってどう定義,あるいは,近似するかを考えればいいわけです.
> 直接ボース凝縮になる条件ではなくて,必要条件ということは理解しました.
必要条件でも十分条件でもありません.(何となく必要条件)
> ボース凝縮になる条件を課すなら,むしろ,逆に古典気体を量子気体とみなせる状況でないといけないのでは?
そうです.つまり「粒子間距離 >>ドブロイ波長」の否定.これは「粒子間距離 <ドブロイ波長」とはなりません.
仮にそうだとしても,「粒子間距離 <ドブロイ波長」でボース凝縮が起こる保証,および「粒子間距離 >ドブロイ波長」でボース凝縮が起らない保証,ともにありません.
あくまでも,目安,第零近似です.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 13:48)
> 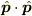 は正の固有値を持つので,
は正の固有値を持つので, 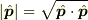 は(第二義的かもしれませんが)意味を持つと思います.
> このとき,
は(第二義的かもしれませんが)意味を持つと思います.
> このとき, ![[\hat q,|\hat{\bm p}|]=i\hbar](http://hooktail.maxwell.jp/bbslog/f4dfae4f7f6e1ecef6955ad6356d7b72.png) となるような演算子
となるような演算子 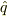 があれば,不確定性関係
>
があれば,不確定性関係
> 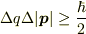 > が成り立つのですが,このような演算子があるかどうかが疑問です.
> が成り立つのですが,このような演算子があるかどうかが疑問です.
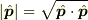 はobservableであるが,第二義的(
はobservableであるが,第二義的( 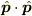 から定義される量)であり,「(正準)運動量」という意味はないかもしれない.
から定義される量)であり,「(正準)運動量」という意味はないかもしれない.
という理解でよろしいでしょうか?
それなら,同意します.
Re: ボース凝縮
yama さんのレス (2008/06/05(Thu) 15:29)
そういうことです.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 17:11)
> ただ,今までの記事からは,「ベクトル演算子である 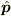 は第二義的で,
は第二義的で, 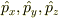 が本質的だ」とおっしゃっているように読めるのですが....
が本質的だ」とおっしゃっているように読めるのですが....
これについてはよくわからないですね.
ベクトル演算子は形式的なものとは思いたくないのですが,今回の様に不確定性関係を導出しようとする場合は直交座標系で計算しなければいけないのなら,座標系に依存する概念となり,「ベクトル」演算子は第二義的なものになってしまいます.
ベクトル演算子の交換関係は座標系に依存しない形で定義可能なのでしょうか?そしてそれは意味があるものでしょうか?意味のある不確定性関係は導けるのでしょうか?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 18:08)
> 意味のある不確定性関係は導けるのでしょうか?
まだ,うまくまとめられないですが,c数テンソル 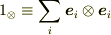 を定義し,
を定義し, 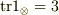 から,
から,
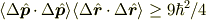
となりそうです.
Re: ボース凝縮
メントス さんのレス (2008/06/05(Thu) 20:50)
>toorisugari no Hiroさん つまり「粒子間距離 >>ドブロイ波長」の否定.これは「粒子間距離 <ドブロイ波長」とはなりません. 「粒子間距離 >>ドブロイ波長」の否定は「粒子間距離 <ドブロイ波長」になるのでは?
ようするに,今の問題では実際にボース凝縮になるかどうかは別として,古典気体を量子気体として扱わなければならないので
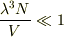 の逆,
の逆, 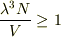 つまり,
つまり, 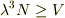 が条件になると考えます.
そうすると,20133の条件は,不等号が逆ではないですか?
が条件になると考えます.
そうすると,20133の条件は,不等号が逆ではないですか?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 21:15)
> 「粒子間距離 >>ドブロイ波長」の否定は「粒子間距離 <ドブロイ波長」になるのでは?
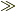 の意味をご存じですか?
の意味をご存じですか?
- 「粒子間距離 >>ドブロイ波長」は日本語で書くと「粒子間距離はドブロイ波長に比べて[非常に]大きい」.よってこの否定は「粒子間距離はドブロイ波長に比べて非常に大きいわけではない.(小さくても,少しぐらいでかくても良い)」
> そうすると,20133の条件は,不等号が逆ではないですか?
これは古典気体の条件として出されていますから問題ないです.( 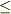 は
は 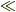 の間違いではないか?という問いは正しいけど些末)
の間違いではないか?という問いは正しいけど些末)
Re: ボース凝縮
メントス さんのレス (2008/06/05(Thu) 21:22)
sergeさんのおっしゃられた条件は古典気体である条件, 私の考える条件は量子気体である条件, 求めるのはその境目の温度だから,どちらで考えても同じ,という理解でよろしいですよね? ようやく問題の意味が見えてきました.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 21:41)
> 求めるのはその境目の温度だから
ついでに言うと,その境目の温度は確定したものではないです.境目はぼんやりして,あくまでも代表値(参考値)として先の値を挙げているだけです.
基本的にこういう議論はオーダーエスティメート,10の何乗程度かを見極めるための議論です. ファクタについてはもっと精密な議論でということ.
# 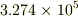 の場合オーダーは5,ファクタは3
の場合オーダーは5,ファクタは3
# 「 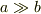 」は「
」は「  のオーダーは
のオーダーは  のオーダーより二つ三つ以上でかい」と読んでもそう間違いではないです.
のオーダーより二つ三つ以上でかい」と読んでもそう間違いではないです.
Re: ボース凝縮
メントス さんのレス (2008/06/05(Thu) 22:05)
>ついでに言うと,その境目の温度は確定したものではないです. はい,気をつけます.
問題に戻ります.今までのことをまとめると
不確定性関係を使うために,1つの方向成分の運動量と位置を考える.等方性によりこの方向を  軸方向にとっても一般性を失わない.
軸方向にとっても一般性を失わない.
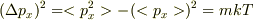
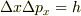 から
から
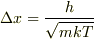 量子気体になる条件から(粒子を球体と半径
量子気体になる条件から(粒子を球体と半径 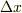 と考える)
と考える)
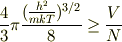
境界の温度は
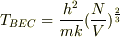 すごい!このモデル計算からちゃんと
すごい!このモデル計算からちゃんと 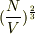 依存性が出てきました.少し感動です.
依存性が出てきました.少し感動です.
まだ,続きの問題があるのですが,4番はどういう風に考えればいいのでしょうか? 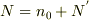 において,
において, 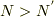 とすればいいのでしょうけど,ボース分布ではなく,マクスウェル統計を使わなければならないと問題に指定されているので,どうやればいいのか分からないです.
とすればいいのでしょうけど,ボース分布ではなく,マクスウェル統計を使わなければならないと問題に指定されているので,どうやればいいのか分からないです.
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 22:13)
細かいですが
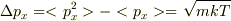 でなく
でなく

あと,ファクターはどうでもいいのだから 「
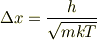
量子気体になる条件から(気体分子の平均距離を 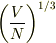 で定義して)
で定義して)
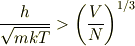
これより境界の温度は
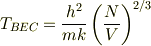
」 でいいのでは?
Re: ボース凝縮
toorisugari no Hiro さんのレス (2008/06/05(Thu) 23:25)
> 不確定性関係を使うために,1つの方向成分の運動量と位置を考える.
は
「
不確定性関係を使うために,1つの方向成分での運動量と位置を考える.等方性によりこの方向を  軸方向にとっても一般性を失わない.
」
にするとより感じが出てきます.
軸方向にとっても一般性を失わない.
」
にするとより感じが出てきます.
Re: ボース凝縮
yama さんのレス (2008/06/05(Thu) 23:58)
不確定性関係についてですが,これは正準共役な座標と運動量について成り立つ関係なので,デカルト座標に限られるわけではなく,座標系に依存するものではないと思います. ただし,古典力学の一般座標が,すべて量子力学の正準座標になるわけではなく,たとえば極座標の動径rは負の値をとらないので正準座標にはならないようですが・・・.
ベクトル量の不確定性関係は,toorisugari no Hiroさんが書かれた式のように表すことができるとは思いますが,その場合は各成分ごとに成り立つ不確定性関係が全体の中に埋もれてしまうように思います, ベクトル量は各成分ごとに不確定性関係が成り立ちますが,これをベクトル演算子のままで1つの式にまとめるのは無理があるように思います.
Re: ボース凝縮
メントス さんのレス (2008/06/06(Fri) 11:15)
> toorisugari no Hiroさん ありがとうございます.記事を修正しておきました.
Re: ボース凝縮
メントス さんのレス (2008/06/07(Sat) 14:13)
少し疑問に思ったのですが,量子気体になる条件
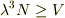 というのは普通の常識で考えたらありえませんよね.
入れ物のなかに,入れ物の体積より多くのものが入ってることになります.
ということは,ボース凝縮が起きてる状態では,粒子の波束が互いに重なり合ってる(というと変かもしれませんが)というふうに,理解すればいいのでしょうか?
というのは普通の常識で考えたらありえませんよね.
入れ物のなかに,入れ物の体積より多くのものが入ってることになります.
ということは,ボース凝縮が起きてる状態では,粒子の波束が互いに重なり合ってる(というと変かもしれませんが)というふうに,理解すればいいのでしょうか?
それと,申し訳ありませんが,NO,20134の4番の問題の解き方の指針を教えてください.よろしくおねがいします.
Re: ボース凝縮
yama さんのレス (2008/06/07(Sat) 14:34)
4番の問題ですが,マクスウェル分布で計算した1粒子の平均エネルギー(3kT/2)が最低エネルギーと同程度になれば,相当数の粒子が基底状態に落ち込むと思われるので,そうなるような温度を求めればいいでしょう.
最低エネルギーは,3次元の井戸型ポテンシャルの中の粒子の基底状態のエネルギーとして求められます.
Re: ボース凝縮
メントス さんのレス (2008/06/07(Sat) 16:01)
ありがとうございます. こういう演習書に載ってないような問題は,言われればなるほど,と思うんですけど,自分ではおもいつかなそうです. 自分の勉強の仕方が浅いのかもしれませんね. N個の粒子全体で考えようとしてましたが,1つの粒子が基底状態をとるような温度ならば,他の粒子たちも同じような状況になるだろう,ということなのですね.
一粒子の基底エネルギーは
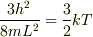 よって粒子が基底エネルギーをとり始める温度は
よって粒子が基底エネルギーをとり始める温度は
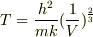 5,粒子数密度を一定にしつつ,粒子数と体積を無限大にする極限での比(3のT/4のT)を求め,なぜそうなるのか理由を述べよ.
5,粒子数密度を一定にしつつ,粒子数と体積を無限大にする極限での比(3のT/4のT)を求め,なぜそうなるのか理由を述べよ.
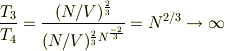
理由は,3番のTは量子気体になるというだけの条件だったため,ボース凝縮が起きていない温度も含んでおり,粒子が基底エネルギーをとり始める温度より,大きいオーダーだから.と考えました.
合ってますでしょうか.
Re: ボース凝縮
yama さんのレス (2008/06/07(Sat) 23:43)
は粒子数に無関係なので,ボーズ凝縮を起こす温度としては正しくありません.これに対して
は正しい粒子数依存性を示しています.
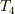 は各粒子が他の粒子と無関係に1粒子の状態関数で表されるものとして求められています.粒子数が少なくて,各粒子の状態関数が重ならないならそのように考えることができるでしょう.
しかし粒子数が多くなって,状態関数(波束)が重なってくると,各粒子の状態関数ではなく,気体全体の状態関数を考えることが必要になってきます.ボーズ粒子の場合,その状態関数は,粒子の互換について対称でないといけません.
ボーズ凝縮には,このような状態関数の対称性が関係していると考えられます.
は各粒子が他の粒子と無関係に1粒子の状態関数で表されるものとして求められています.粒子数が少なくて,各粒子の状態関数が重ならないならそのように考えることができるでしょう.
しかし粒子数が多くなって,状態関数(波束)が重なってくると,各粒子の状態関数ではなく,気体全体の状態関数を考えることが必要になってきます.ボーズ粒子の場合,その状態関数は,粒子の互換について対称でないといけません.
ボーズ凝縮には,このような状態関数の対称性が関係していると考えられます.
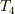 は,このような波束の重なりを考えないで求めたものなので,粒子数に無関係な値になったのでしょう.
は,このような波束の重なりを考えないで求めたものなので,粒子数に無関係な値になったのでしょう.
Re: ボース凝縮
メントス さんのレス (2008/06/08(Sun) 00:58)
ええと, 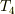 に粒子依存性が出てこなかったのは,私の間違いじゃなくて,そういう問題だってことでいいんですよね?
に粒子依存性が出てこなかったのは,私の間違いじゃなくて,そういう問題だってことでいいんですよね?
Re: ボース凝縮
yama さんのレス (2008/06/08(Sun) 08:49)
そうだと思います.
Re: ボース凝縮
メントス さんのレス (2008/06/08(Sun) 14:10)
一週間にわたって付き合ってくださり, yamaさん,sergeさん,toorisugari no Hiroさんありがとうございました. 一つの問題から多くのことが学べました.
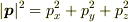
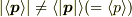 を誤解されていたように思います.
を誤解されていたように思います.