テルレッツキーの不変速度

テルレッツキーの不変速度

toorisugari no Hiro さんの書込 (2008/05/31(Sat) 02:34)

例のスレッドに重ねようかと思いましたが，別にします． テルレッツキーのローレンツ変換の導出，読みました．「光速不変の原理」を使わず，相対性原理だけでローレンツ変換の大枠を導き出してますね．

座標変換

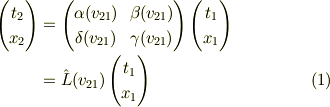
\begin{pmatrix}t_2 \\ x_2\end{pmatrix} &=\begin{pmatrix}\alpha(v_{21}) & \beta(v_{21}) \\\delta(v_{21}) & \gamma(v_{21})\end{pmatrix}\begin{pmatrix}t_1 \\ x_1\end{pmatrix}\\&= \hat L(v_{21}) \begin{pmatrix}t_1 \\ x_1\end{pmatrix}\tag{1}

に条件

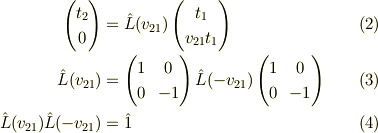
\begin{pmatrix}t_2 \\ 0\end{pmatrix}&= \hat L(v_{21}) \begin{pmatrix}t_1 \\ v_{21}t_1\end{pmatrix}\tag{2}\\\hat L(v_{21}) &=\begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \hat L(-v_{21})\begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \tag{3}\\\hat L(v_{21}) \hat L(-v_{21}) &= \hat 1 \tag{4}

((3)は空間反転による不変性，(4)は 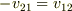-v_{21}=v_{12} より，系1から2への変換は系2から1への逆変換であること，を示しています．)を適用して， 通常なら，さらに，光速不変則

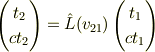
\begin{pmatrix}t_2 \\ c t_2\end{pmatrix}&= \hat L(v_{21}) \begin{pmatrix}t_1 \\ c t_1\end{pmatrix}

を使うところを， 代わりに，相対性原理「異なる系から見ても変換則(1)は不変である．」

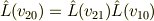
\hat L(v_{20}) &= \hat L(v_{21})\hat L(v_{10})

を用いて v によらない速度が存在することを導いています．また，この速度を光速にすればそのままローレンツ変換になります．

# 具体的な計算を見たい方は杉山さんのページ

の

を見てください．

これは光速不変則を使わずローレンツ変換を導いたと言うより，相対性原理を満たす時空における座標変換の一般的性質を導いたものですね．

特殊相対論のローレンツ変換だけでなく古典力学のガリレイ変換も不変速度無限大の極限で上の理論に含まれますから．