微分形のガウスの法則に関する問題

微分形のガウスの法則に関する問題

T.U さんの書込 (2008/05/30(Fri) 17:24)

電磁力学を独学で学んでいる社会人ですが，微分形のガウスの法則でどうしても判らない問題があるので教えて下さい．

この問題は例解：電磁力学演習の４３ｐにあり

”厚さ２ｄの無限に広い平らな板の内部に，電荷が一様な密度ｐで分散している．微分形のガウスの法則を用いて，このとき，板の内外の点に生じる電場を求めよ”という問題ですが，

解答は”板の面に垂直にｘ軸を，板の中心に原点Ｏをとる．電荷分布の対象性により，電場Ｅはｘ軸方向を向き，その強さはｙ,ｚ座標に依存しない．そこで，電場の強さをＥ（Ｘ）とおくと，ネブラ・Ｅ＝ｄＥ（ｘ）／ｄｘであるから，微分形ガウスの方程式は”

｜ｘ｜＞ｄ（つまり板の外部）のとき，ｄＥ（Ｘ）／ｄｘ＝０であると書かれています．

板の内部の方程式は質問と関係ないので割愛します．

板の外では電場はｘ（板の中心からの距離）に関係なく一定と書かれていますが，これは下記の点電荷のつくる電場の式（距離（ｒ）によって電場が変化する）と矛盾する気がしますが，これはどうやって理解すべきものなのか，教えて頂けたらたすかります．

Ｅ（ｒ）＝ｑ１＊｜ｒ−ｒ１｜ −−−−−−−−−− ４πE0｜ｒ−ｒ１｜＾３

Re: 微分形のガウスの法則に関する問題

yama さんのレス (2008/05/31(Sat) 00:20)

点電荷が１個だけの場合は，電場の強さは点電荷からの距離の２乗に反比例します． しかし，問題になっている場合は，多数の点電荷が板の内部に分布していると考えることができるので，それら多数の点電荷のつくる電場を重ね合わせたものが観測される電場になります． つまり各点電荷がつくる電場をクーロンの法則によって計算し，それをベクトル的に合成するわけです．無限個の点電荷が連続的に分布しているので，積分を計算することになりますが，実際に計算してみれば，板からの距離に関係なく一定になることが分かります． 平面上に電荷が分布しているときの電場の計算は大抵の電磁気学の本にのっていると思います． 板の内部にも電荷がある場合は，無限に薄い多数の板に分割して考えればいいでしょう．（薄い板を平面と見なすわけです．）

もちろんガウスの法則を利用するほうが簡単に電場を求めることができます． 直観的には電気力線を考えると分かりやすいでしょう． 点電荷からは，電気力線が無限遠に向かって放射状に広がります． 点電荷を中心とする球面を考えると，その面積は半径の２乗に比例するので，電気力線の密度は点電荷からの距離の２乗に反比例することになり，従って電場の強さも距離の２乗に反比例することになります． 点電荷が平面上に分布している場合は，対称性から，電気力線は平面に垂直で，真っ直ぐに無限遠に向かいます．そのため，電気力線の密度（従って電場の強さ）は，平面からの距離に関係なく一定になります 厚みのある板の場合は，平面分布の電荷が多数集まったものと考えると，この場合も板からの距離に関係なく電場の強さが一定になることが理解できるでしょう．，

Re: 微分形のガウスの法則に関する問題

toorisugari no Hiro さんのレス (2008/05/31(Sat) 01:41)

yamaさんのご説明で十分にご理解できたと思いますが，蛇足をします．

平板から離れた点(高さ 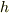h )の電場の大きさが 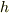h によらないことを「感覚的に」示します．

いま，点を頂点とする円錐を考えます．平板に垂直な軸と表面のなす角は任意でいいですが，ここでは60度としましょう．底面の円は平板上にあります．

いま，「円の中にある電荷だけが，電場に寄与する」と仮定します．底面円の半径は高さ 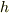h に比例する(60度の場合 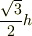\frac{\sqrt{3}}{2} h )ので，面積，そして，電荷は 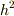h^2 に比例します．

いま，円錐を相似に保ったまま，点の高さを 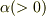\alpha(>0) 倍にします．影響を与える電荷は 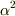\alpha^2 倍になります．平板までの距離は \alpha 倍になります．

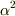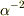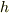「クーロンの法則」より電場にたいする電荷の寄与が \alpha^2 倍，距離の寄与は \alpha^{-2} 倍になり，相殺されて電場の大きさは \alpha によらないこと，つまり h によらないことが導き出されます．

# 同じように線電荷のつくる電場が距離の逆数になることも導けます．

先ほどの仮定が気持ち悪いなら，以下のように考えてください． 円錐ではなく，例えば60度と70度の2重円錐(底面はドーナツ)を考えても，上の議論はそのまま成り立ちます．

これは0度と10度の(2重)円錐,10度と20度の2重円錐,,,,80度と85度の2重円錐,85度と88度の2重円錐,88度と89度の2重円錐,,,,でも同様(距離によらない)です．

これらを足し合わせると，ほぼ全平面の電荷を考えることになります．よって，平板上の電荷が作る電場は距離によらないことが導かれます．

なお以上のことを数式で表すと

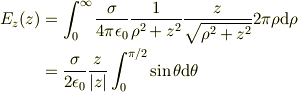
E_z(z)&=\int_0^{\infty}\frac{\sigma}{4\pi\epsilon_0}\frac{1}{\rho^2+z^2} \frac{z}{\sqrt{\rho^2+z^2}} 2\pi\rho\mathrm{d}\rho \\&= \frac{\sigma}{2\epsilon_0}\frac{z}{|z|}\int_0^{\pi/2}\sin\theta\mathrm{d}\theta

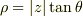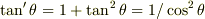です．(最後の式は \rho=|z|\tan\theta , \tan'\theta = 1+\tan^2\theta = 1/\cos^2\theta を使いました．)

Re: 微分形のガウスの法則に関する問題

T.U さんのレス (2008/06/02(Mon) 14:47)

yamaさん，tourisugariさん，

大変丁寧な説明をして頂きありがとうございました．

やっと理解できました．

T.U