ドッグ さんの書込 (2008/05/28(Wed) 11:24)

x*y + sin(x+y) - log(√1+x*x+y*y) = 2, x*x + x + x*y + 1 = 0

連立非線形方程式を満たす解(近似解)を２つ求めよ．

という問題なのですが，解ける方教えてください．

toorisugari no Hiro さんのレス (2008/05/28(Wed) 13:46)

数値計算としての問題なら， まずグラフソフトを使ってグラフを描いてあたりをつけるというのが定番です．

しかし，描いてみると．．．．変ですね．式，書き写し間違いしてませんか?

tip★ さんのレス (2008/05/28(Wed) 14:45)

自分なら，ニュートン法を使いますね．

初期値が必要なんで，まずはgnuplotあたりでプロットしたほうがいいと思います．

陰関数のプロット・・・難しいそうですね！！！

toorisugari no Hiro さんのレス (2008/05/28(Wed) 17:46)

最終的にニュートン法を使うにしても，初期値を適切に決めないと使い物にならないのは有名な話． で，gnuplotで初期値のあたりをつける．

set cont base set nosurf set cntrp lev disc 0 set view 1,0 splot x*y + sin(x+y) - log(sqrt(1+x*x+y*y))-2, x*x + x + x*y + 1

とすると．．．．． 0等高線の有限の角度で交差する交点は存在しない．つまり，解なし． (描画精度の問題かもしれないが．．．)

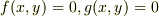# の解をニュートン法で求めるためには一階微分行列の逆行列が存在，つまり， ，0等高線が有限の角度で交差，する必要が有ります．

なんとなく さんのレス (2008/05/29(Thu) 12:00)

こんにちは．なんとなくです． toorisugari no Hiroさんお仰るとおり，解が無いようです． 一変数で考えたら良いと思います．

x*y + sin(x+y) - log(√1+x*x+y*y) = 2・・・? x*x + x + x*y + 1 = 0・・・? ?からx≠0(x=0は解にならない）ので， x*y=-(x*x+x+1),x+y=-(x+1/x)となるので，?式から f(x)=x*x+x+1+sin(x+1/x)+(1/2)log{(1+x*x+(x+1/x+1)^2}+2 と置いて，f(x)=0の解．|sin(...)|≦1，logの中は1より大などより f(x)>0，つまり解は無いと思います．