フジモリ さんの書込 (2008/05/27(Tue) 18:32)

「時空比一定の定理」は名称として分かり難いとの指摘があり，「時空比普遍の定理」に改めました．ごく単純な定理ですが決定版を再掲します．

単純化のため直線上を相対速度vで等速運動している慣性座標系S1(x1,t1),S2(x2,t2)を考え，それぞれのx軸の正方向を同じ方向にとり，原点を一致させる．両座標系の特性を調べる． S1(x1座標)から見たS2の原点(x2=0)の運動は x1=v*t1 であるから，x2は因数 (x1-v*t1) をもつ．よって x2=γ(x1-v*t1)(1a) γ はvの未知関数で，v→0のときγ→1(v>0,γ≠1)，また空間の等方性よりγ(v)=γ(-v)．(1a)と同様に x1=γ(x2+v*t2)(1b) (1a)(1b)を γ(v)=γ(-v) の対称性を用いて変形する．γ(v)=x2/(x1-v*t1)=γ(-v) だから x2=γ(x1+v*t1)(2a) x1=γ(x2-v*t2)(2b) [(1a)(1b)(2a)(2b)はx,tの４元同次一次連立方程式で，その解は原点(t1=x1=t2=x2=0)にある． △削除6.1] 変数変換 xi=ci*ti (ci=時空比)を行いその特性を調べる．両辺を掛け合わせて (1a)*(1b)c2*c1=γ^2(c1-v)(c2+v)(3a) (2a)*(2b)c2*c1=γ^2(c1+v)(c2-v)(3b) (1a)*(2b)c2*c1=γ^2(c1-v)(c2-v)(4a) (2a)*(1b)c2*c1=γ^2(c1+v)(c2+v)(4b)

(3a)(3b)を連立させて v(c1-c2)=0,c1=c2[=C>0] (4a)(4b)を連立させて v(c1+c2)=0,c1=-c2 結局c1=±c2となるので，相対的慣性座標系は時空の特性として共通の時空比定数+C,-Cを持つ． (3a)は時空比定数Cを用いて C^2/γ^2=(C-v)(C+v) >0 (5) よって-C<v<C, γ=1/√(1-v^2/C^2) >=1等号はv=0のとき(6)

工学部系の旧師を通して専門家にも検討を頼みました．

フジモリ さんのレス (2008/05/27(Tue) 18:34)

議論が収束したと思ったのは間違いでした．

４元同次一次連立方程式(条件v>0,γ≠1)は原点合わせをして式を立てたので解は原点です． >(1a), (1b), (2a), (2b) で原点でなくても t1=t2=0, x1=x2 であれば解になるようですがNo.20004 >(1a), (1b), (2a), (2b) が連立方程式として，同時に満たされるのは，t1=t2=0,γ=1,x1=x2 の場合に限られるように思われますがNo.19986 →どう解くとそうなるのか道筋を数式で示して下さい．おかしい所が指摘できるかもしれません．

>また，この場合には時空比一定の定理とも両立しません →解の存在とは別に，式の性質が抽出されることは両立します．例えば，連立方程式x=y, x=-y の解は原点ですが，両者は直交しているという性質が導けます．

>そもそもフジモリさんの議論は，基本的なレベルでの矛盾が多いことは >他者による善意的拡大解釈を経て，何とか既存の理論に収まることが確認できただけです →包括的，主観的な断定よりも具体的，客観的な反論を提示すべきです．善意は結構ですが，おかしな点を指摘することを優先して下さい．

>つまり共通の値が速度vの関数になる可能性が排除できないからです． →v(c1-c2)=0を導き，最後にv≠0で除しているので，速度には依存しません．

toorisugari no Hiro さんのレス (2008/05/27(Tue) 19:31)

フジモリさん もうやめませんか?

>>(1a), (1b), (2a), (2b) が連立方程式として，同時に満たされるのは，t1=t2=0,γ=1,x1=x2 の場合に限られるように思われますがNo.19986 > →どう解くとそうなるのか道筋を数式で示して下さい．おかしい所が指摘できるかもしれません．

これをご自分でcheckして確かめることのできない算数力ではこれ以上の議論は無駄だと思います．(新定理とかいってる場合ではないです．)

フジモリ さんのレス (2008/05/27(Tue) 21:47)

toorisugari no Hiro さん，それは卑怯というものでしょう． toorisugari no Hiro さんは， >>(1a), (1b), (2a), (2b) が連立方程式として，同時に満たされるのは，t1=t2=0,γ=1,x1=x2 の場合に限られるように思われますが(No.19986) を正しいと思っているのか，間違いと思っているのか不明確ですが，どちらですか．(1a), (1b), (2a), (2b) の連立方程式の解についてはNo.19986,No.19988,No.19998,No.20004,No.20012,No.20017と毎回のように蒸し返されて，その都度解は原点にあると指摘しました．小生の初等代数の知識を以てすれば，あり得ない話が延々と続いている訳でして，何か群論などの高等な道具を使えば，そう結論されるのかとも疑って数式で提示するよう要請した次第です．No.19986について言えば，γ=1はガリレイ変換に帰結することになりますが，v>0の条件で検討している訳ですから，γ≠1を検討すべきであり，そうすれば計算しなくとも論理で「x1=x2=0に限る」が解となります．どういう論理で「t1=t2=0,γ=1,x1=x2 の場合に限られる」のか「限られる」理由を是非数式を提示してお答え下さい．そうすれば，こちらでその間違いを指摘します．この問題はまだ決着してはいないのです．

yama さんのレス (2008/05/27(Tue) 23:47)

原点が解の場合は，t1=t2=0, x1=x2=0 を(1a)〜(2b)に代入すると，すべての式が 0=γ*0 になってしまうので，γの値が定まりません．γの値を定めるには，原点以外の解を検討する必要があります．

原点以外の解を求めるために x1≠0 の場合を考えます． t1=t2=0 になることはご承知だと思いますので，これを(1a)と(1b)に代入すると x2=γ*x1(1a)' x1=γ*x2(1b)' となりますが，(1a)'を(1b)'に代入すると x1=γ^2*x1 となり，x1≠0 と仮定しているので γ^2=1すなわち，γ=±1 となりますが，v→0のときγ→1 だとすると結局 γ=1 が得られます．従って γ≠1 を検討する余地はありません． また aを0でない任意の定数として，γ=1, t1=0, t2=0, x1=a, x2=a を(1a)〜(2b)に代入すると，すべての式が満たされるので，これが確かに解で あることが分かりますが，この解は原点ではありません．

上記の計算は初等代数しか用いていないので

>これをご自分でcheckして確かめることのできない算数力ではこれ以上の議論は無駄だと思います．(新定理とかいってる場合ではないです．)

という toorisugari no Hiroさんの意見に賛成せざるを得ません．

>v(c1-c2)=0を導き，最後にv≠0で除しているので，速度には依存しません．

それは単に c1=c2 を導いただけで，それがvに無関係な定数であることの証明にはなっていません．

また以前に

>>γ(v)=γ(-v) ということは，γ(v)の中のvを-vに置き換えてもかまわないということですが，γ(v)の外のvまで-vに置き換えてもかまわないということではありません． >→よい点をご指摘戴きました．論理を改めます．

というやりとりがあったにも関わらず，今回も同じ間違いをされているのは残念です．

>工学部系の旧師を通して専門家にも検討を頼みました．

何の専門家か存じませんが，高校生でも分かるような間違いを指摘されなかったのでしょうか？だとするとフジモリさんにとってはまことにお気の毒なことと言わざるをえません． それとも，まだ検討した結果を受け取られていないのでしょうか？ それだったら検討結果が分かるまで投稿を控えてほしかったと思いますが・・・．

フジモリ さんのレス (2008/05/28(Wed) 20:37)

>γの値を定めるには，原点以外の解を検討する必要があります． →話をそらさないで下さい．連立方程式(1a), (1b), (2a), (2b) の解の問題を論じています． (1a)'を(1b)'に代入すると x1=γ^2*x1即ちx1(γ^2-1)=0, よって x1=0(このときx2=0) 又は γ=±1←解 原点が確かに解になっています．γ=±1は特別な場合として最後に検討すればよい．γ=±1のとき原式(1a), (1b)はガリレイ変換となるが，ここではγ≠±1として検討を進めます．初等代数の計算というより，論理の進め方の問題でしょう．小生の(1a)から(6)に至る本論の障害にはなりません． >「連立方程式の解がt1=t2=0,γ=1,x1=x2 の場合に限られる」No.19986 などという必然性は全くありません．

>v(c1-c2)=0を導き，最後にv≠0で除しているので，速度には依存しません． c1=x1/t1であり，ここにvが含まれないことで，vには依らないc1であると言えます．

>>γ(v)=γ(-v) ということは，γ(v)の中のvを-vに置き換えてもかまわないということですが，γ(v)の外のvまで-vに置き換えてもかまわないということではありません． →γ(v)^2=γ(-v)^2は必ずしも成り立たないので，論理から外しました． 一般に ax+f(x)=1 で f(x)=f(-x)のとき問題なく a*(-x)+f(-x)=1 が成り立ちます．上記の主張で「γ(v)の外のvまで-vに置き換えてもかまわないということではありません」とはどういうことですか．

>まだ検討した結果を受け取られていないのでしょうか →当初皆さんが小生の考えをすぐに理解してくれるだろうと思っていたところ，その逆なので人を介してさる人に「急ぎませんがご検討下さい」と頼みました．結果は勿論お知らせします．それとは独立に皆さんの疑問に答え，またはこちらから反論することは，本掲示板の主旨に添うものであると思います． 立論は極めて単純至極ですので，小生に間違いがあれば本筋でご指摘頂けたらと思ってNo.20043を投稿しました．

yama さんのレス (2008/05/29(Thu) 00:43)

>→話をそらさないで下さい．連立方程式(1a), (1b), (2a), (2b) の解の問題を論じています． >(1a)'を(1b)'に代入すると >x1=γ^2*x1即ちx1(γ^2-1)=0, よって x1=0(このときx2=0) 又は γ=±1←解

x1=0 も解ですが，その場合は，γの値が決まらないので，x1≠0 として解を求めるとγ=1 になるということです． もちろんγ≠±1という条件を加えれば，この条件を満たすx1≠0の解は存在しないことになります．しかし，この条件は連立方程式とは別に与えられたものなので，純粋に連立方程式だけを考えれば，aを0でない任意の定数として，γ=1, t1=0, t2=0, x1=a, x2=a も解であると言えます．

>>「連立方程式の解がt1=t2=0,γ=1,x1=x2 の場合に限られる」No.19986 >などという必然性は全くありません．

それは確かにその通りで，t1=t2=0,x1=x2=0 という解もありますね．しかし，この解ではγの値が決まりません． 「γの値が定まる解は t1=t2=0,γ=1,x1=x2 の場合に限られる」 とすべきでしょうね． もし，t1=t2=0,x1=x2=0 であれば，連立方程式からは γ=1/√(1-v^2/C^2) でなければならないことは導けません． なぜなら「γ=1/√(1-v^2/C^2) でなければならない」ということは，これ以外の場合は連立方程式が満たされないということですが，γ=1/√(1-v^2/C^2)でなくても，たとえばγ=1/√(1+v^4/C^4), t1=t2=0,x1=x2=0 としても，連立方程式のすべての式が満たされることは明らかです． t1=t2=0,x1=x2=0 であれば，γがどんな値であっても成り立つ方程式を，どういじくり回しても，γが特定の値でなければならないという結論が導けるはずがありません． ところが，フジモリさんは γ=1/√(1-v^2/C^2) が導けるとしています．導けるはずのないものが導けるということはどこかに間違いがあると言わざるをえません．

たとえば変数変換 xi=ci*ti ですが，t1=t2=0だからciの値は定まりません． ti≠0ならば，ciの値は定まりますが，その場合は連立方程式自体が成り立ちません． 「ti≠0のときは，連立方程式は成り立たないが，かわりにA.B,C・・・などの関係式が成り立つ．そこでこれらA.B,C・・・を用いると・・・」というように進めるなら話は分かりますが，フジモリさんは成り立たない方程式を，あたかも成り立つかのようにそのまま用いています．しかし，成り立たない方程式から何を導いても無意味です．

>c1=x1/t1であり，ここにvが含まれないことで，vには依らないc1であると言えます．

この論法が成り立つとすると「円の面積S=πr^2であり，ここに円周の長さLが含まれていないことで，Lには依らないSであると言えます．」ということになります．

>→γ(v)^2=γ(-v)^2は必ずしも成り立たないので，論理から外しました． 一般に ax+f(x)=1 で f(x)=f(-x)のとき問題なく a(-x)+f(-x)=1 が成り立ちます．

それが正しいとすると，たとえば f(x)=2x^2 については f(x)=f(-x) が成り立つので 「ax+2x^2=1 のとき a(-x)+2(-x)^2=1」 が成り立つことになります． しかし，a=-1, x=1のときは，ax+2x^2=1 は成り立つにもかかわらず a(-x)+2(-x)^2=1 は成り立ちません．

>→当初皆さんが小生の考えをすぐに理解してくれるだろうと思っていたところ，その逆なので人を介してさる人に「急ぎませんがご検討下さい」と頼みました．

誰からも理解されないのは，自分の考えが間違っているためではないかとはお考えにならなかったのでしょうか． もちろん多くの人々に批判されながらも結局は正しかったという学説も歴史上にはあります．しかしそんな例は希であって，多くの場合は何らかの欠陥があったために批判されたのです． 謙虚な気持ちで批判を受け止めることが大切だと思います． なぜ批判されるのかも理解できない学力レベルで，間違った理論を延々と展開し反論にもならない間違った理屈を並べているような状態が本掲示板の主旨に添うものであるかどうかは疑問です． 相手にせずに放置しておけばいいのかもしれませんが，それでは間違った説をそのまま黙認した形になるので，途中でさじを投げるわけにもいかず，不毛なやりとりを続けているわけです． 言論・表現の自由のためには，掲示板のこのような状態も許容しなければならないのだろうとは思いますが，ただただ空しく思います．

せめて専門家の検討結果が分かるまでこれ以上の投稿は控えてほしいと願うのみです．

toorisugari no Hiro さんのレス (2008/05/29(Thu) 12:23)

不定問題 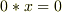の解は何でも有りです．どんな結果も出せますが，すべて無意味です．(要するに何も言えない．)

前にフジモリさんに大学初年者向けの参考書を紹介しましたが，忘れてください． 不定問題や0除算を計算して平気なんて中学生並の学力といわれても仕方有りません．なので，上の本は無理です．高校生向けの参考書で一次方程式の係数による解の場合分け，連立方程式と行列式の関係，を勉強しなおしてください． (ま，仮に勉強し直したとしても，座標変換の間違った理解もしているので道は遠いですが．．．)

フジモリ さんのレス (2008/05/29(Thu) 21:48)

>前にフジモリさんに大学初年者向けの参考書を紹介しましたが，忘れてください． →余計なご心配は無用です．紹介の労に感謝の言葉をお返ししましたが，紹介の本を勉強してみようなどとはさらさら思っていませんし，その意思も表明してはいません．学窓を出て以来，必要なことを必要な範囲で勉強するのもままならぬ身なれば．

>(No.19936)特殊相対論は量子論がからまないかぎり数学的構造がはっきりわかっています．少なくとも学部レベルで扱える数学的枠組みの中では新しい「公式」などは出ません． →「光なしの相対論」というのがあるという投稿を見ました．苦労している先人がいるんですね．この問題に決着がついているのでしょうか．世の中の書籍には「光速度不変の原理」しか載っていません．こういう実際的な情報こそ今回の議論に直結した価値があります．同じようなことを考えた人がいるなんて，勉強してみたくなります．

>中学生の学力といわれても仕方有りません →人間は間違える動物．こういう言葉の手裏剣を人に向かって投げつければ，廻りまわって自分の眉間に還ります．

toorisugari no Hiroさん，あなたも識見ある武士(もののふ)なら，頓珍漢な横槍を入れたり，割り込んで切り捨てたりする狼藉ではなく，僅か二十行の論理の矛盾を，正々堂々と正面から数式と論理を以て衝いたらどうですか．私は自説に固執している訳ではありません．ただ納得したいだけです．不定問題が具体的に何を指すのか不明ですが，数式掲示板です．数式も提示しないで，やれ高校生だ中学生だと居丈高に物言うことは，私のビジネスの世界ではこけおどしと言うんです．オチコボレの法則に共鳴して来た者としては，創設者の意思を継ぐべくあくまで数式と論理を通して議論したいと思います．

MXK さんのレス (2008/05/29(Thu) 23:17)

記事No.20045で出されていた，反論のための例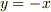， , ですが，これを両辺それぞれ割り算すると 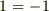という無意味な結果になってしまいます． これは連立方程式の解が 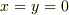であることを忘れて，ゼロでの割り算を行っているからです．

この等式 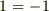を認めると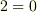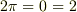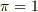， , , , 「 は整数である」, 「任意の無理数は整数である」などなど，言いたい放題になります．

傾きの議論をされていましたが，その場合は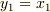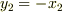， , とおいて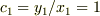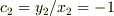， , と傾きを求め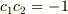， から，直交していることを示すべきです．

4つの式の連立に疑問を投げかけ，それを解消する方向を示唆したつもりですが，連立方程式に一層拘っておられることに 驚いています．

佐藤 さんのレス (2008/05/30(Fri) 00:27)

フジモリさま，みなさま こんばんは． 相対論を勉強している最中の学生です．

論理自体の疑問はみなさまがおっしゃっているのでいいませんが フジモリさんにひとつお願いがあり書き込みを致しました．

みなさまのおっしゃっている質問・疑問に対してしっかりとお答え下さい． フジモリさんの議論を見ているとみなさまの質問の意味を理解していないように見えます． フジモリさんに対してみなさまが何度も同じ質問をしていることからも明らかだと思います．

なので今一度みなさまの質問に対して自分の論理が正しいという考えを一先ず置いてお答えになられてはいかがでしょうか？

学生の身分でこんなことを言ってしまい気分を害されたらすいません． 議論が噛み合っていないことを見ていられなくて思わず書き込みをしてしまいました．

よろしくお願いします．

管理人さま 不適切な書き込みならば削除していただいて構いません．

失礼しました．

yama さんのレス (2008/05/30(Fri) 00:47)

>→解の存在とは別に，式の性質が抽出されることは両立します．例えば，連立方程式x=y, x=-y の解は原点ですが，両者は直交しているという性質が導けます．

私もこれについてコメントしておきます． 確かに x=y と x=-y のグラフは直交します． しかし，そのことにどんな意味があるのでしょうか？

x=y を２倍して x=-y に加えると 3x=y が得られます． 逆に 3x=y から x=-y を引いて２で割ると x=y が得られます． つまり， x=y, x=-y (1) と 3x=y, x=-y(2) の２組の連立方程式を考えると，(1)から(2)を導くことができ，逆に(2)から(1)を導くことができるので，この２組の連立方程式は同値です． ということは，連立方程式(1)を連立方程式(2)で置き換えることができるわけです． しかし，(2)のグラフは直交しません． つまり，グラフが直交するという性質は，もとの方程式をそれと同値な別の形に変形しただけで失われてしまうわけです． こんなかりそめの性質は，方程式自体の性質とは言えないのでほとんど無意味だと思います．

意味があるのは，同値な方程式に共通な性質です． (1)も(2)もグラフが原点で交わるという点では共通なので，グラフが原点で交わるという性質は意味があるでしょう． しかし，この性質は方程式の解が原点 x=y=0 にあるという当たり前のことを意味しているにすぎません．

toorisugari no Hiro さんのレス (2008/05/30(Fri) 10:24)

> 僅か二十行の論理の矛盾を，正々堂々と正面から数式と論理を以て衝いたらどうですか．

>> 不定問題 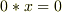の解は何でも有りです．どんな結果も出せますが，すべて無意味です．(要するに何も言えない．)

まさか，僅か二行の数式と論理の意味を，および，それを以て「定理」の矛盾を衝いてるのを，理解できないのでしょうか?

フジモリ さんのレス (2008/05/30(Fri) 17:33)

toorisugari no Hiroさん， そう勿体をつけないで単刀直入に平易にご説明願えませんか．

toorisugari no Hiro さんのレス (2008/05/30(Fri) 18:39)

> そう勿体をつけないで単刀直入に平易にご説明願えませんか．

これ以上「単刀直入に平易に」って何が有るんでしょう? つまり， 「まさか，僅か二行の数式と論理の意味を，および，それを以て「定理」の矛盾を衝いてるのを，理解できないのでしょうか?」 これは危惧ではなく事実なのですね．

まさか って思ってはいないですよね．

フジモリ さんのレス (2008/05/31(Sat) 10:10)

>t1=t2=0,x1=x2=0 であれば，γがどんな値であっても成り立つ方程式を，どういじくり回しても，γが特定の値でなければならないという結論が導けるはずがありません．No.20064 →γが特定の値とはなっていません．Cの値は特定されません．γの値は連立方程式からは決まりません．これで解に対する疑問は解消しましたか．

>たとえば変数変換 xi=ci*ti ですが，t1=t2=0だからciの値は定まりません．No.20064 →変数変換のことですが，数式上のテクニックでより簡潔に式が表現でき，また見通せるので使ったまでで，変数変換せずに原式のまま変形して，積の形でt2*x1=t1*x2 を容易に導けます．

>a=-1, x=1のときは，ax+2x^2=1 は成り立つにもかかわらず a(-x)+2(-x)^2=1 は成り立ちませんNo.20064 →成り立つのは勿論「方程式」です．方程式a(-x)+2(-x)^2=1 が成り立ちます．

>謙虚な気持ちで批判を受け止めることが大切だと思いますNo.20064 →その通りです．「不毛なやりとりを続け」ない為にも数式と論理に基づく検証をすべきだと思いますが，一般論や中高生論は多くても，提示した数式や論理上の具体的指摘が少ないのです．

>これは連立方程式の解が x=y=0 であることを忘れて，ゼロでの割り算を行っているからですNo.20074 →(1a)から(6)に至る数式の展開で，割り算は変数変換だけですが，上述の如く変数変換をしなくても同じ結果が得られます．どこかでゼロの割り算を行ってその結果を用いていることがあればご指摘下さい．

>議論が噛み合っていないことを No.20075 →小生の間違いの部分もあり，そこは修正しましたので，数式と論理を以て一つひとつ誤解を解き又は致命的間違いを発見したいと思います．真理は一つです．

>傾きの議論をされていましたが，その場合は・・・No.20074 >こんなかりそめの性質は，方程式自体の性質とは言えないのでほとんど無意味だと思いますNo.20076 →4つの連立方程式から無限の変形ができ，その殆どは無意味でしょう．ただし4つの方程式を「すべて」含む(3a)(3b)を連立させて得た集約関係式t2*x1=t1*x2 (c1=c2に相当)と，(4a)(4b)を連立させて得た集約関係式t2*x1=-t1*x2 (c1=-c2に相当)は原点解を含むシンプルな関係で，この関係を無意味と棄てることができなかったのです．これらの関係は連立方程式が成立する限り常に成立し，二つの慣性系の時間と空間の関係を示す重要な情報と解しました．

toorisugari no Hiro さんのレス (2008/05/31(Sat) 13:48)

> ただし4つの方程式を「すべて」含む(3a)(3b)を連立させて得た集約関係式 > t2*x1=t1*x2 (c1=c2に相当)と，(4a)(4b)を連立させて得た集約関係式 > t2*x1=-t1*x2 (c1=-c2に相当)は原点解を含むシンプルな関係で， > この関係を無意味と棄てることができなかったのです．

x1=x2=t1=t2=0とした時点ですべて無意味です． つまりc1=0/0,c2=0/0という無意味な関係しか得られません．

何故無意味かというと，c1=c2でもc1=5*c2でもc1=-c2でもc1=-5*c2でもなりたち，どれかが正しいとかどれかが間違いとか一切言えないからです．

例 5*0=0だから c1 = 0/0 = (5*0)/0 = 5*(0/0) = 5*c2

0/0を使って何か意味のあること導いたと言う人は「嘘つき」か「無知」のどちらかの称号で呼ばれることでしょう．

> これらの関係は連立方程式が成立する限り常に成立し，
> 二つの慣性系の時間と空間の関係を示す重要な情報と解しました．

あなたにとって都合がいいってだけでしょ．自分の都合で数学の論理を破っています．

論理や数式とおっしゃるあなたが論理や数式を無視してる．

こういうのは無手勝流といいません．「出鱈目」です．塚原さんに無礼です．

yama さんのレス (2008/05/31(Sat) 15:07)

>→γが特定の値とはなっていません．Cの値は特定されません．γの値は連立方程式からは決まりません．これで解に対する疑問は解消しましたか．

特定の値というのは特定の具体的な数値という意味で用いたのではないのですが，揚げ足をとられてしまったようですね． t1=t2=0,x1=x2=0 であれば，γがどんな値（一般にはvの関数）であっても方程式が成り立つので，γ=1/√(1-v^2/C^2) でなければならないということは導けないということです．

>→変数変換のことですが，数式上のテクニックでより簡潔に式が表現でき，また見通せるので使ったまでで，変数変換せずに原式のまま変形して，積の形でt2*x1=t1*x2 を容易に導けます．

その原式が t1=t2=0 でない場合には成り立たないことが問題なのです． t2*x1=t1*x2 は t1=t2=0 のときは 0*x1=0*x2 という当たり前の式になってしまいます． t1=t2=0 でない場合にも成り立つことを示すには，t1=t2=0 でない場合に成り立つ式に基づかないといけません．しかしフジモリさんは t1=t2=0 でない場合にどんな式が成り立つのか示されていません． t1=t2=0 の場合にしか成り立たない原式を，t1=t2=0 でない場合にも成り立つかのように用いているだけです． しかし，成り立たない式に基づいて何を導いても無意味です．

→成り立つのは勿論「方程式」です．方程式a(-x)+2(-x)^2=1 が成り立ちます．

意味がよく分かりませんが，a(-x)+2(-x)^2=1 は ax+2x^2=1 とは別の方程式で同じ解を持つ必要はないということでしょうか． だとすると，両方が同時に成り立つわけではありませんね．（x=0 または x=±b が解になる場合は同時に成り立ちますが） しかし，フジモリさんは，vを-vで置き換えた式を，もとの式と連立させていますね．連立するということは同時に成り立つということですが・・・． ところでvは慣性系間の相対速度であって，任意の値をとりうるのだと思っていましたが(1a)(1b)はvの特定の値についてしか成り立たない方程式なのでしょうか？ これがvについての方程式で，ｖを-vで置き換えた方程式(2a)(2b)も同時に成り立つとすれば，この方程式には v=0 という解がありますね． 確かに v=0 なら(1a)〜(1b)のすべての式が満たされるし，t2*x1=t1*x2 も成り立ちます．しかしそれがどんな意味があるのでしょうか？

>→(1a)から(6)に至る数式の展開で，割り算は変数変換だけですが，上述の如く変数変換をしなくても同じ結果が得られます．どこかでゼロの割り算を行ってその結果を用いていることがあればご指摘下さい．

既に述べたように連立方程式(1a)〜(2b)は（v=0 の場合を除いて）t1=t2=0 の場合にしか成り立ちません． 従ってt2*x1=t1*x2 は t1=t2=0 の場合についてしか証明されていません． t2*x1=t1*x2 をc1*t2=c2*t1 と書き直して t1=t2=0 を代入すると c1*0=c2*0 になります．両辺を0で割らないとしたら，どのようにしてc1=c2 が導けるのでしょうか？ c1=c2 でなくて，たとえば c1=2c2 であっても c1*0=c2*0 は成り立ちますが・・・．

>→小生の間違いの部分もあり，そこは修正しましたので，数式と論理を以て一つひとつ誤解を解き又は致命的間違いを発見したいと思います．真理は一つです．

誤解をしているのはフジモリさんだと思います． 致命的な間違いは，vを-vで置き換えた式がもとの式と同時に成り立つとしている点です．（v=0の場合とか，原点とかでは例外的に成り立ちますが）

>(4a)(4b)を連立させて得た集約関係式t2*x1=-t1*x2 (c1=-c2に相当)は原点解を含むシンプルな関係で，この関係を無意味と棄てることができなかったのです．

無意味です．棄てて下さい．シンプルな関係だから成り立つとは言えません．