「交換子群の記事」について

「交換子群の記事」について

pono さんの書込 (2008/05/26(Mon) 13:09)

初めて投稿します．よろしくお願いします．

こちら（物理のかぎしっぽ）の「交換子群の記事」についてなのですが，

最初に「交換子群が群になること」を示しているのですが， 群の定義「演算について閉じている」を示す時に 演算として「交換子を取る操作」としています．

そして結合則が成り立つのは明らかとしていますが，

演算として「交換子を取る操作」とした時には 群の定義の結合則は (a*b)*c＝{aba(-1)b(-1)}*c＝aba(-1)b(-1)cbab(-1)a(-1)c(-1) a*(b*c)＝a*{bcb(-1)c(-1)}＝abcb(-1)c(-1)a(-1)cbc(-1)b(-1) なり，成り立たないと思うのですが，どうでしょうか？

Re: 「交換子群の記事」について

スチーム さんのレス (2008/05/27(Tue) 00:30)

数学には素人なので，ちょうど私も同様の疑問をもったのですが， 交換子群が部分群になるのですから，演算はもとの群で定義されたものと同じではないでしょうか． そうすると，結合法則は自然と成り立ちます． この解釈でいいのでしょうか． 数学に詳しい方のコメントよろしくお願いします．

Re: 「交換子群の記事」について

mNeji さんのレス (2008/05/27(Tue) 14:04)

皆さん，こんにちは．少し，インチキな感じで考えて見ましたので，途中まで書いてみます．

交換子の逆元があれば，

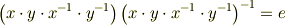
\left( x\cdot y \cdot x^{-1} \cdot y^{-1} \right) \left( x\cdot y \cdot x^{-1} \cdot y^{-1} \right) ^{-1} = e

を満たす筈です．

そこで両辺の左から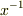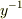， x^{-1} ， y^{-1} ， x ， y ，を順番に掛けて整理して行くと，逆元を陽に表す事ができますね．

先ず 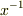x^{-1} を左から掛けると

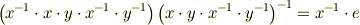
\left(x^{-1} \cdot x\cdot y \cdot x^{-1} \cdot y^{-1} \right) \left( x\cdot y \cdot x^{-1} \cdot y^{-1} \right) ^{-1} = x^{-1} \cdot e

整理して，

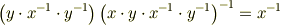
\left( y \cdot x^{-1} \cdot y^{-1} \right) \left( x\cdot y \cdot x^{-1} \cdot y^{-1} \right) ^{-1} = x^{-1}

同様にして...

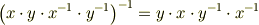
\left( x\cdot y \cdot x^{-1} \cdot y^{-1} \right) ^{-1} = y \cdot x \cdot y^{-1} \cdot x^{-1}

と陽に表示できます．まさに逆元は，各成分を逆に入れ替えられた状態ですね．

以下，省略．

Re: 「交換子群の記事」について

pono さんのレス (2008/05/27(Tue) 17:41)

すみませんが，逆元ではなくて，結合則に関してです． よろしくお願いします．

Re: 「交換子群の記事」について

mNeji さんのレス (2008/05/27(Tue) 18:32)

自分では計算していませんが，この場合の結合則とは

左辺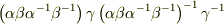＝ \left( \alpha\beta\alpha^{-1}\beta^{-1} \right)\gamma \left( \alpha\beta\alpha^{-1}\beta^{-1} \right)^{-1}\gamma^{-1}

右辺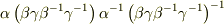＝ \alpha \left( \beta\gamma\beta^{-1}\gamma^{-1} \right)\alpha^{-1} \left( \beta\gamma\beta^{-1}\gamma^{-1} \right)^{-1}

との等号関係を示すものではないでしょうか？間違っているかも知れませんが...．

Re: 「交換子群の記事」について

pono さんのレス (2008/05/28(Wed) 18:35)

>との等号関係を示すものではないでしょうか？

そうだと思うのですが，αとγの数が違うので， 「左辺＝右辺」は成り立たないと思うのですが．

Re: 「交換子群の記事」について

mNeji さんのレス (2008/05/28(Wed) 19:16)

>そうだと思うのですが，αとγの数が違うので，

そうですよね．でも恒等式；

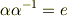
\alpha\alpha^{-1}=e

見たいな関係を考慮すると，要素の数にはあまり拘らなくても善いのかなとかんじるのですが．

Re: 「交換子群の記事」について

スチーム さんのレス (2008/05/29(Thu) 09:00)

ponpさんもmNejiさんも計算に間違いはないとおもいます． 問題の原因は以下のところにあるのではと感じました．

本文中の， ＞また，G の元の積に関して結合則はなりたつはずなので，D(G）の元の交換子積でも結合則がなりたつことは明らかです．

ここは交換子積ではなく， 「もとの群で定義されたもの」とすべきではないでしょうか． 交換子積の操作は群の生成にのみ用いられるべきと思います．

Re: 「交換子群の記事」について

toorisugari no Hiro さんのレス (2008/05/29(Thu) 13:33)

(部分群の演算は) > 「もとの群で定義されたもの」とすべきではないでしょうか． > 交換子積の操作は群の生成にのみ用いられるべきと思います．

私も賛成です．しかし，部分群であるためには演算で閉じていないといけないわけで，それを私は

\forall ~ a,b,c,d \in G,~\exists~ X,Y \in G\text{ s.t. } [a,b][c,d]=[X,Y]

と理解しているのですが，一般的に示せません．なにかまちがっているのでしょうか？

それともこれは個々の具体的な問題で示すまで先送りにし，ひとまず，閉じていると仮定して話を進めているのでしょうか？

Re: 「交換子群の記事」について

pono さんのレス (2008/05/29(Thu) 20:07)

私もその後調べまして

交換子群の定義は「群Gにおける全ての交換子によって『生成される』Gの部分群」 と定義されています． ここで『生成される』の定義を考えると，

例えばa,b,c,c∈Gにおいて aba^(-1)b^(-1) cdc^(-1)d^(-1)はそれぞれ交換子です．

そして群の定義よりこの2つを演算した 「aba^(-1)b^(-1)cdc^(-1)d^(-1)」も交換子群の元になります．

つまり 交換子は交換子群の元ですが， 交換子群の元は交換子のみではないということだと理解しました．

まだ勉強中ですので間違えている可能性もあります．

Re: 「交換子群の記事」について

mNeji さんのレス (2008/05/30(Fri) 02:40)

前回のケースは成り立ちませんでした．さらに次の拡大解釈をしてみましたが駄目でした．

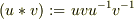(u*v) := uvu^{-1}v^{-1} として

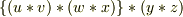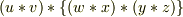\left\{ (u*v)*(w*x) \right\}*(y*z) と (u*v)*\left\{ (w*x)*(y*z) \right\} とが等しいと予測しましたが，成立しませんでした．

〜〜〜〜 何度か手計算を書いているうちに逆操作，「^(-1)」が間違いやすいので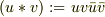， (u*v) := uv\bar u \bar v とすると，比較的エラーが低減できました．と同時に交換関係の無い，複素数表現にも見えそうで...．

Re: 「交換子群の記事」について

通りすがり さんのレス (2008/06/02(Mon) 08:28)

＞交換子群の元は交換子のみではないということだと理解しました．

この解釈であってるようだ． 私も読んでいて戸惑ったのだけど，「交換子群がたしかに群になること」の説明として ＞交換子を取る操作に対して，交換子群は閉じています ってのがあるのが変なんだと思う． この説明だと，交換子群の演算が「交換子を取る操作」であるかのように見えてしまう． これは交換子群の性質であって，「交換子群がたしかに群になること」の理由ではない．

なお，交換子群がたしかに群になるのは，交換子を生成元として生成された群なんだから，単に当たり前の話である．

Re: 「交換子群の記事」について

toorisugari no Hiro さんのレス (2008/06/03(Tue) 11:14)

> なお，交換子群がたしかに群になるのは，交換子を生成元として生成された群なんだから，単に当たり前の話である．

「生成する」って言葉をちゃんとしらべてなかったのが問題でしたね．

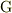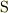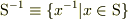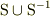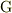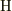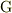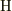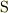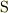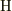「群 \mathrm{G} の空でない部分集合を \mathrm{S} ， \mathrm{S}^{-1}\equiv\{x^{-1}|x\in\mathrm{S}\} とする． \mathrm{S}\cup\mathrm{S}^{-1} の有限個の元の積として表される \mathrm{G} の部分集合 \mathrm{H} は \mathrm{G} の部分群である． \mathrm{H} を \mathrm{S} によって生成される部分群， \mathrm{S} を \mathrm{H} の生成系，という．」

ですね．

[a,b]=aba^{-1}b^{-1} とすれば， [a,b]^{-1}=[b,a] なので， [\mathrm{G},\mathrm{G}]=\{[x,y]|x,y\in\mathrm{G}\} とすれば [\mathrm{G},\mathrm{G}]=[\mathrm{G},\mathrm{G}]^{-1}

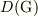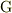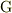よって， D(\mathrm{G}) とは [\mathrm{G},\mathrm{G}] の有限個の元の積として表される \mathrm{G} の部分集合，すなわち， e(=[a,a]),\,[a,b],\,..,\,[a_1,b_1][a_2,b_2]\cdots[a_n,b_n],\,... の全体なんですね．そりゃ，群 \mathrm{G} の演算，積，に関して閉じてること，単位元・逆元の存在，積に関する結合則，全部あたりまえだ．

Re: 「交換子群の記事」について

anon さんのレス (2008/06/05(Thu) 14:17)

ponoさんの最初の疑問に関してです．

No.20103 の通りすがりさんも仰っているように， 「交換子を取る操作に対して，交換子群は閉じている」という説明は， 文脈に合っていませんね．

「交換子を取る操作に対して，交換子群は閉じている」というのは要するに 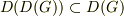D(D(G)) \subset D(G) ということを云っているのですから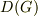， D(G) の演算とは関係ないですよね．

手直ししたほうがよろしいのではないかと思います．