しそ さんの書込 (2008/05/23(Fri) 18:14)

高校生です．

• http://www.phys-challenge.jp/img/pdf/jikken-q2008-1.pdf の所に

連成振り子の実験があります． ここの実験について質問です． ここの図においておもりＣを重くしたらどうなりますか． またAEを長くしたらどうなりますか． またECを長くしたらどうなりますか． またEFを長くしたらどうなりますか．

よくわからないんです. 勉強し始めたばかりですので，分かりやすく書いていただけると幸いで

toorisugari no Hiro さんのレス (2008/05/24(Sat) 18:44)

2度，同じ質問をされてますね．せっかくですが，この質問に答えることは一切できません．物理チャレンジ参加者の迷惑になるからです．

レポートの締め切りから数日後でしたら何らかの回答ができるかもしれません．もし，そのときになってもまだ興味が有るようでしたら，この後ろに質問をつけてください．

しそ さんのレス (2008/06/07(Sat) 17:42)

toorisugari no Hiro さんすいません．

toorisugari no Hiro さんのレス (2008/06/07(Sat) 19:55)

この質問のことでしょうか？

>  http://www.phys-challenge.jp/img/pdf/jikken-q2008-1.pdf の所に
> 連成振り子の実験があります．

(PDFがみられない方のために，装置の概略をかくと， 天井のある程度離れた2点A,Bに同じ長さの糸をつり，同じ質量のおもりC,Dをつなぎます．AC,BD間のかなりA,B寄りのところの同じ高さの点E,Fを少し張り気味に糸でつなぎます．)

> ここの実験について質問です．
> ここの図においておもりＣを重くしたらどうなりますか．
> またAEを長くしたらどうなりますか．
> またECを長くしたらどうなりますか．
> またEFを長くしたらどうなりますか．

しそさんがどういう目的でご質問されたかも不明ですが，単に関心があるからということなら，答えを必要とするわけではないですよね．物理チャレンジとどのような関係があるかも予想できないので，迂闊に教えるわけにもいきません．

それにこの掲示板の方針もあるので，答えを出すつもりはありません．

ヒントを出しますから，考えてください．「わかりません」でなく，わかるところまで答えてくれてたら，さらにヒントが出せるかもしれません．

> ここの図においておもりＣを重くしたらどうなりますか．

もし，単独の振り子ならどうなるでしょうか?振動の様子で変わるところはありますか?

この振り子の上部に糸を水平につないで引っ張ったとき，水平な糸に掛かる力はおもりの質量の変化に対してどう変わりますか?

単独の振り子を手で振動させた場合，力の大きさと振れの関係はどうなりますか?

> またAEを長くしたらどうなりますか．

ECの長さを変えないで，ですか?

同位相のときと，逆位相のとき，どのような振れ方をするか，考えてみてください．

まだAEを変えないで， (それぞれの場合に対して，)E(F)はどう動きますか? (それぞれの場合に対して，)振れの周期に違いはありますか?

AEを変えたら， D(C)の振り子の運動の周期はどう変わりますか?

> またECを長くしたらどうなりますか．

AEの長さを変えないで，ですか?

とりあえず，ヒントは上の問いに準じます．

> またEFを長くしたらどうなりますか．

さあ，どうなるでしょう?考えてみてください．

DIO さんのレス (2008/06/07(Sat) 23:28)

この運動を解析しようとしたのですが，，難しいです． （ここで具体的なこと書いて良いんでしょうか??）

これは高校程度の知識で解けるんでしょうか

この課題は主に高校生向けでしょうから解けると思われるのですが

yama さんのレス (2008/06/08(Sun) 00:02)

実験を行って，それをレポートにまとめるという課題なので，実験から規則性を見いだすことが必要ですが，その規則性が生じる理由を数学的に完全に解析して説明する必要はないと思います． 実験結果についての考察はもちろん必要ですが，高校物理のレベルで可能な範囲の考察でよいと思います．

DIO さんのレス (2008/06/08(Sun) 09:35)

数学的な解析は高校物理のレベルでは難しいということでしょうか？

私は参加者じゃないのですが，興味があって考えてます．

糸EC,FDと鉛直方向のなす角を 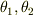としてそれについて解こうとしているのですが， おもりC,Dの運動方程式と点E,Fのつり合いの式だけでは解けないんでしょうか

yama さんのレス (2008/06/08(Sun) 11:07)

点E,Fにはたらく力はつり合っていないと思います．

DIO さんのレス (2008/06/08(Sun) 17:26)

点E,Fを質量0と考えました．

しそ さんのレス (2008/06/08(Sun) 20:05)

考えると同位相の周期の場合，逆位相の周期よりも短いと思います．とすると片方揺らした場合は（うなり)と考えてよいのですか？そうすると，この現象は共振と言われていますけれど共振ではないと考えていいのでしょうか？

(僕は高校１年生です．友達が物理チャレンジを受けると言っていたので，最近興味を持っています．今までくわしいことを言わなくてすいません）

toorisugari no Hiro さんのレス (2008/06/09(Mon) 19:25)

高校一年生ですか，その割には > 考えると同位相の周期の場合，逆位相の周期よりも短いと思います．とすると片方揺らした場合は（うなり)と考えてよいのですか？そうすると，この現象は共振と言われていますけれど共振ではないと考えていいのでしょうか？ 鋭い考察ですね．

振幅が小さいときには振り子は単振動とみなせますが，これはフックの法則=比例則，が成り立ちます．こういうシステムを線形というのですが，線形なシステムには重ね合わせの原理という非常に強力な考え方ができます．

しそさんは片方揺らした場合を，同位相と逆位相の重ね合わせと考えて上の結論を出されたわけですね．慧眼だと思います．

本来の共振は片方の運動を固定(一定振動，一定振幅)するので，確かに厳密な意味での共振ではありません．