単振り子
単振り子
DIO さんの書込 (2008/05/21(Wed) 00:20)
単振り子の運動方程式としてよくθが微少の時
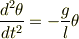
と表されますがこれの導出についてお尋ねしたいです
xy平面でy軸と振り子のなす角をθ,おもりの質量をm,張力をTとします
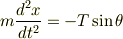
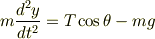
としてx,yを三角関数で表すと
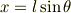
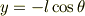
運動方程式はそれぞれ
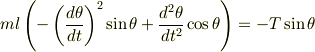
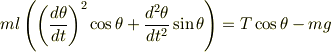
となり,?×cosθ+?×sinθをすると
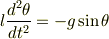
これでθ微少とすると一番上の式になります
ところが以下のようにしている教科書がありました
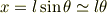
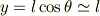
と,先に近似し,これを運動方程式に代入し
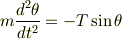
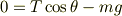
としていました.ここからTを消せば同じ結果が得られるのですが, この式は正しいのでしょうか? 一番最後の式は
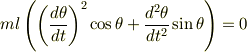
を言っていることになると思うのですが,どう考えてもこの式は成り立ちません
アドバイスよろしくお願いします
Re: 単振り子
toorisugari no Hiro さんのレス (2008/05/21(Wed) 00:34)
> 一番最後の式は
> 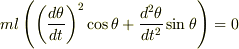 > を言っていることになると思うのですが,どう考えてもこの式は成り立ちません
> を言っていることになると思うのですが,どう考えてもこの式は成り立ちません
 を微少量と考えれば上の式の左辺は
を微少量と考えれば上の式の左辺は  の二次のオーダーです.つまり上式は
の二次のオーダーです.つまり上式は  の一次のオーダーで成り立ちます.(誤差は
の一次のオーダーで成り立ちます.(誤差は  の二次のオーダー)
の二次のオーダー)
Re: 単振り子
DIO さんのレス (2008/05/21(Wed) 17:00)
>toorisugari no Hiroさん
返信ありがとうございます
お陰で理解できました
θが20°〜30°と設定してたので誤差が大きかったみたいです
Re: 単振り子
DIO さんのレス (2008/05/24(Sat) 21:33)
すみません,もう一度質問させてください.
>を微少量と考えれば上の式の左辺はの二次のオーダーです.つまり上式はの一次のオーダーで成り立ちます.(誤差はの二次のオーダー)
ということはθ微少の場合θの微分も微少と見なせると言うことでしょうか??
これが単振動であると既知の場合はθは三角関数なので上記のことが成り立つのは分かるのですが
一般に微少と見なせる  について
について 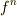 も微少とできるのでしょうか??
も微少とできるのでしょうか??
Re: 単振り子
toorisugari no Hiro さんのレス (2008/05/24(Sat) 22:22)
を微小パラメータとして
とおきます.
の大きさは1のオーダーであるとします.
すると, 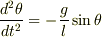 は
は  の一次のオーダーで
の一次のオーダーで

となります.
このとき
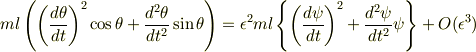
となります.この右辺に近似方程式(a)の解を代入すると,かっこの中は1のオーダーになることがわかるので,  の一次のオーダーで左辺の値は0になります.
の一次のオーダーで左辺の値は0になります.
> ということはθ微少の場合θの微分も微少と見なせると言うことでしょうか?? > これが単振動であると既知の場合はθは三角関数なので上記のことが成り立つのは分かるのですが > 一般に微少と見なせる |8fa14cdd754f91cc6554c9e71929cce7| について |bd8f6c1f3e77d1688430334b62512c22| も微少とできるのでしょうか??
まったく,正統な疑問です.答えは,「うまくいけばそれでよし.もしうまくいかないようなら,改めて近似を考え直す.」です.
実際  の次のオーダーまで考えた解を出す場合,
(これは
の次のオーダーまで考えた解を出す場合,
(これは
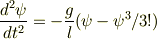
を解くことに相当します ) 今までの素朴な近似法(単純摂動法)では破綻します.(エネルギーの保存則が破れ発散する,つまり,心配が実現してしまう.)
これは「永年項(共鳴項)問題」と呼ばれる問題で,解決には多重摂動法という新しい数学が必要でした.
これをここで説明するのは無理ですが,簡単に触れると
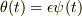 のかわりに,
のかわりに, 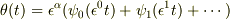 で考える(
で考える(  は計算がうまくいくように,共鳴項が消えるように,決める)というものです.
は計算がうまくいくように,共鳴項が消えるように,決める)というものです.
これは周期の振幅変化を考えるということに相当します.
Re: 単振り子
komagatake さんのレス (2008/05/26(Mon) 09:15)
DIOさん
>θが20°〜30°と設定してたので誤差が大きかったみたいです
これはどういう意味でしょうか. 御質問の内容と合わないように思います. 測定をされたのでしょうか.
ご質問は単振動の式を求めるのに「先に近似を使ってもいいのか」というものです.
測定をされたのであれば その角度が近似の成り立つ範囲内かというのが問題になります. 20°〜30°という角度は近似の成り立つ範囲から出ています. 近似の成り立つ範囲から出たときにどういう結果が得られるのかという問題意識での実験であればずれは当然予測されていますから誤差とは言いません.誤差とは測定誤差の意味ですよね.誤差は実験の信頼性を表す言葉です.精度のいい実験をやればずれは目立ってきますので「誤差」とは別のことだというのが分かるはずです.
横軸に角度,縦軸に周期をとってグラフを書けば周期一定の水平のグラフが徐々に上にずれていくはずです.sinθ<θですから単振動で考えた時よりも復元力が弱くなっています.周期が長くなります.20°〜30°ではこのずれがはっきりと見えてきていると思います.高等学校でやるレベルの,糸とおもり,ストップウオッチを使った周期の測定でも分かります. 角度が小さくて近似が十分に成り立っていると考えられるところで測定した時に測定値と式による計算値とが合わないとします.この場合には誤差という言葉を使ってもいいでしょう.ここで測定の精度をチェックする事になります.θ〜5°程度であれば十分に近似が成り立っていますから測定精度のチェックが出来ます.
近似的なモデルで得た式による値と測定値とのずれを「誤差」と言う人がかなりいるように思いますので気になりました.
気体の性質の測定でも理想気体の状態方程式から予想される値からのずれが出てきます.これに対しても誤差という言葉を使っているのを見ます.これは誤差ではありません.近似の荒さが測定にかかってきたということのはずです.
測定の荒さと近似の荒さは区別して考える必要があります.
Re: 単振り子
DIO さんのレス (2008/05/28(Wed) 13:22)
>toorisugari no Hiroさん
返信が遅れました,申し訳ありません.
永年項(共鳴項)問題というのは初めて聞きました. 難しそうですが,参考になりました.ありがとうございます.
>komagatakeさん
実際に測定したわけではないんですが
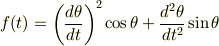
をPCで計算ました.
この時|2554a2bb846cffd697389e5dc8912759|の初期値を20°〜30°にしてたらf(t)は大きくなってしまったわけです
誤差と言う言葉はおかしかったようですね,ご指摘ありがとうございます. 以後気を付けます
Re: 単振り子
toorisugari no Hiro さんのレス (2008/05/29(Thu) 13:59)
誤差には「測定誤差」のほかに「打ち切り誤差」という概念も有るので,DIOさんの使い方も間違いではないです.計算機を使うなら他に「丸め誤差」も有りますが.測定誤差に対してこれらを計算誤差といいます.