キリングベクトル

キリングベクトル

竹見台 さんの書込 (2008/05/20(Tue) 21:33)

はじめまして．学部３年の者です．物理学科ではないのですが，相対論に興味があり独学しています．

もしかしたら数学の質問になってしまうかもしれませんが・・・

小玉英雄先生の相対性理論(培風館)のP208の(8.25)式

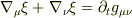
\nabla_{\mu} \xi +\nabla_{\nu} \xi = \partial_{t} g_{\mu \nu}

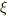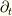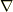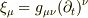
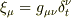
についてです．ここで \xi は時間座標 t の座標基底 \partial_{t} です．また \nabla は共変微分です．この本によると，この式は一般的に成り立つそうなのですが，まず座標基底の定義から 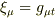\xi_{\mu} = g_{\mu \nu} (\partial_{t})^{\nu} \xi_{\mu} = g_{\mu \nu} \delta^{\nu}_{t} \xi_{\mu} = g_{\mu t} となると思います．すると 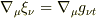\nabla_{\mu} \xi_{\nu} =\nabla_{\mu} g_{\nu t} となりますが，計量テンソルの共変微分は常にゼロになるので，結局 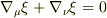\nabla_{\mu} \xi +\nabla_{\nu} \xi = 0 が得られてしまいます．いったい何がおかしいのでしょうか？他の本を当たっても同じような話題が載っておらず，困っています．どなたかお願いします．

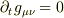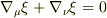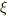ちなみに上の本では，時空が定常的で計量が時間によらないとき， \partial_{t} g_{\mu \nu}=0 となるから \nabla_{\mu} \xi +\nabla_{\nu} \xi = 0 であり，このとき \xi はキリングベクトルとなる，と書いてあります．

Re: キリングベクトル

竹見台 さんのレス (2008/05/20(Tue) 21:37)

式の訂正です．

\nabla_{\mu} \xi_{\nu}+ \nabla_{\nu} \xi_{\mu} = \partial_{t} g_{\mu \nu}

でした．すみません．

Re: キリングベクトル

toorisugari no Hiro さんのレス (2008/05/21(Wed) 00:56)

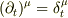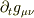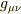私の知っている設定と違うのではずしているかもしれませんが， (\partial_t)^\mu=\delta_t^\mu が違うように思えます． ＃ t は別の座標系， \partial_{t} g_{\mu \nu} の g_{\mu \nu} も別の座標系での表現ではないのですか?

Re: キリングベクトル

竹見台 さんのレス (2008/05/21(Wed) 23:47)

返信ありがとうございます．

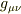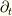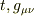t と g_{\mu \nu} が別の座標系での表現というのは， \partial_{t} における t と t, g_{\mu \nu} における t が別のものだということでしょうか．考えてみたのですが，文脈から判断すると恐らくそれは無いと思います．

上記の本から，一部のみそのまま抜粋します↓

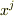「時間的に定常的な時空では，適当に時間座標 t と空間座標 x^{j} をとると，時空計量の成分は空間座標のみに依存すると考えられる:

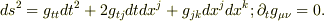ds^2=g_{tt}dt^2+2g_{tj}dtdx^{j}+g_{jk}dx^{j}dx^{k}; \partial_{t}g_{\mu \nu}=0. (8.24)

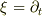一般に， \xi=\partial_{t} に対して

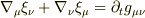\nabla_{\mu}\xi_{\nu}+\nabla_{\nu}\xi_{\mu}=\partial_{t}g_{\mu \nu} (8.25)

が成り立つので，時間座標の並進に対応する無限小変換 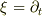\xi=\partial_{t} は計量(8.24)のキリングベクトルとなる．・・・」

というようなことが書いてあります．ただ，リー微分の公式:

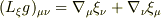
(L_{\xi}g)_{\mu \nu}=\nabla_{\mu}\xi_{\nu}+\nabla_{\nu}\xi_{\mu}

によると確かに

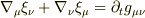
\nabla_{\mu}\xi_{\nu}+\nabla_{\nu}\xi_{\mu}=\partial_{t}g_{\mu \nu}

となるような気もしますし・・・．何がなんだか分からなくなってきました(^^;

Re: キリングベクトル

toorisugari no Hiro さんのレス (2008/05/22(Thu) 13:06)

ううむ．ちなみに私が参考にしたのは内山龍雄さんの「一般相対性理論」のp138です．

私がリー微分を理解していない，つまり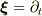， \bm{\xi}=\partial_{t} に対して，

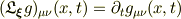
(\mathfrak{L}_{\bm{\xi}}g)_{\mu \nu}(x,t) = \partial_{t}g_{\mu \nu}(x,t)

となるであろう等式の，右辺と左辺の意味の違いを正しく理解できていない(あるいは等式が間違っているかどうかがわからない)ので，これ以上は降参です．

Re: キリングベクトル

yama さんのレス (2008/05/24(Sat) 20:29)

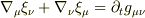
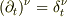一般座標の基底ベクトルは必ずしも単位ベクトルではないので， (\partial_t)^{\nu}=\delta_t^{\nu} は成り立たないのではないでしょうか．