相対論 時空比一定の定理
相対論 時空比一定の定理
フジモリ さんの書込 (2008/05/18(Sun) 07:12)
時空比一定の定理( No.19923の,より分りやすい証明)
S3(x2,t2)S2 ______________・________________・________________・_____________ x ←-vS1v→ (x1,t1)
S1,S2,S3 の慣性座標系を考える.S1,S2の相対速度を v>0 ,S1,S3の相対速度を -v とする.S1から見てS2,S3は空間の等方性と座標系の対称性により座標軸(x2,t2)を共有する.S1(x1座標)から見たS2の原点(x2=0)の運動は x1=v*t1 であるから,x2は因数 (x1-v*t1) をもつ.よって x2=γ(x1-v*t1)(1a) 但し γ はvの未知関数で,v→0のときγ→1,またγ(v)=γ(-v).(1a)と同様に x1=γ(x2+v*t2)(1b)以上再掲 S1,S3の関係は上式をv→-vと置き換えて,γ(v)=γ(-v)だから x2=γ(x1+v*t1)(2a) x1=γ(x2-v*t2)(2b) 見かけ上x,tの同次一次[連立 △削除6.1]方程式であるから,変数変換ci=xi/ti(=時空比)を行いその特性を調べる. (1a)*(1b) c2*c1=γ^2(c1-v)(c2+v)(3a) (2a)*(2b) c2*c1=γ^2(c1+v)(c2-v)(3b)
(1a)*(2b) c2*c1=γ^2(c1-v)(c2-v)(4a) (1b)*(2a) c1*c2=γ^2(c2+v)(c1+v)(4b) (3a)(3b)を連立させて v(c1-c2)=0,c1=c2[=C>0] (4a)(4b)を連立させて v(c1+c2)=0,c1=-c2
結局c1=±c2となるので,相対的慣性座標系は時空の特性として共通の時空比定数+C,-Cを持つ. (3a)は時空比定数Cを用いて C^2/γ^2=(C-v)(C+v) >=0 (5) よって-C<=v=<C を得る. 以上
>(No.19936)特殊相対論は量子論がからまないかぎり数学的構造がはっきりわかっています.少なくとも学部レベルで扱える数学的枠組みの中では新しい「公式」などは出ません.
小生の相対論は大昔教養物理で聞きかじった程度,使っている数学は高校代数程度ですが,無手勝流でこんな定理が出ました.この方面の数学的構造に興味を持ちましたが,どんな文献や資料があるでしょうか.
ところで,英語の物理掲示板でお勧めのサイトをご存知でしたら,お教え下さい.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/18(Sun) 09:03)
>S1から見てS2,S3は空間の等方性と座標系の対称性により座標軸(x2,t2)を共有する.
ここが間違っていると思います. そのため,それ以降の推論も正しくありません.
ローレンツ変換はミンコフスキー空間の座標系の回転であって,座標系S1を(xt平面内で)ある向きに回転させたものが座標系S2で,逆向きに回転させたものが座標系S3です.S2とS3では座標軸の向きが異なるので,座標軸は共有されません.
Re: 相対論 時空比一定の定理
toorisugari no Hiro さんのレス (2008/05/19(Mon) 13:22)
>>(No.19936)特殊相対論は量子論がからまないかぎり数学的構造がはっきりわかっています.少なくとも学部レベルで扱える数学的枠組みの中では新しい「公式」などは出ません.
>小生の相対論は大昔教養物理で聞きかじった程度,使っている数学は高校代数程度ですが,無手勝流でこんな定理が出ました.この方面の数学的構造に興味を持ちましたが,どんな文献や資料があるでしょうか.
高度な数学に興味を持たれるのは良いことですが,力のないまま手を出しても無意味です.
まず,大学初学年で習う線形代数,基礎解析(テーラー展開,双曲関数と三角関数の関係,複素関数論の初歩)および群論の初歩をしっかり学ばれる(復習される)べきだと思います.最初から数学書に当たるのが厳しいのなら,簡単な物理数学の教科書 たとえば 「よくわかる物理数学の基本と仕組み-物理,工学のための数学入門」 潮秀樹 秀和システム
「物理数学とは何か」 和田正信他 裳華房
を読まれてから進まれるのがいいと思います.
そして線形代数を以下の本で学ばれることをおすすめします. 「線型代数入門」 齋藤 正彦
この本が十分に理解出来ないうちは先に進むべきではありません.
あと,気になってたのですが,ローレンツ変換自身をよく理解されてないように思います.相対論を正しく理解されないと,その上に何を建てても無意味です. 手頃な入門書として 「相対論的物理学のききどころ」和田純夫
等がありますから,まずこれで全貌を正しく理解してください.
Re: 相対論 時空比一定の定理
フジモリ さんのレス (2008/05/20(Tue) 18:28)
専門書の紹介有難うございました.群論は初学ですので見当がつきません.
>気になってたのですが,ローレンツ変換自身をよく理解されてないように思います >ローレンツ変換はミンコフスキー空間の座標系の回転であって, いま論じていることはローレンツ変換に至るその前のごく基本的な所です.
>>S1から見てS2,S3は空間の等方性と座標系の対称性により座標軸(x2,t2)を共有する. yama さん,これは表現がまずかったので,次に訂正します. 「相対速度vで運動中の慣性系S1,S2の関係は,式(1a)(1b)に表されるが,式(2a)(2b)でも表される.それはS1から見て,S2であるのかS3であるのか区別がつかないという空間の特性からくる条件である.」
従来の論考は専ら式(1a)(1b)からローレンツ変換を導く方に進みますが,S1を基準系とした場合相手系はS2,S3のどちらでもよい,要するに区別がつかないことを,空間の存在条件として表現しないのは,不十分であると思います.S2,S3は慣性系として同時には存在していなくても,空間としての無区別の特性は存在している訳ですから,時空の特性を見るときは考慮の要があります.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/20(Tue) 21:03)
S1から見るとS2とS3は互いに逆向きに進んでいるので区別できます. 図の場合はS1と基準にすると,S2はv,S3は-vの速度で動いているわけです. もちろん速度成分の値は座標軸の向きのとりかたによって変わるので,x軸の向きを逆にすればS2は-v,S3はvの速度で動くことになります. しかし,座標軸の向きが異なる場合の式が同時に成り立つわけではありません. 座標の文字を変えない場合は,座標軸の向きは固定して考える必要があります.その場合座標軸の正の向きに動くか負の向きに動くかという区別があるわけです.
空間は等方的なので座標軸の向きをどの向きにとってもかまいませんが,一旦向きを決めればそれで座標系が決まるのでその座標系によって運動を記述したりすることになります. もし途中で座標軸の向きを変えれば,異なる座標系に変わることになります.その場合はxのかわりにx'とするなど,座標の文字を変えて区別する必要があります.
Re: 相対論 時空比一定の定理
MXK さんのレス (2008/05/21(Wed) 00:39)
(1a), (1b), (2a), (2b) が連立方程式として,同時に満たされるのは,( 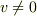 とすると,)
とすると,)
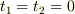 ,
, 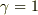 ,
, 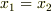 の場合に限られるように
思われますが,いかがでしょう?
すると,(意味のよく分からない)時空比は無限大ということになります.
の場合に限られるように
思われますが,いかがでしょう?
すると,(意味のよく分からない)時空比は無限大ということになります.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/21(Wed) 01:07)
確かにそうなりますね.
Re: 相対論 時空比一定の定理
フジモリ さんのレス (2008/05/21(Wed) 16:31)
>(1a), (1b), (2a), (2b) が連立方程式として,同時に満たされるのは,・・・・・・ の場合に限られるように思われますが,いかがでしょう? →(1a), (1b)又は(1a), (1b), (2a), (2b)はもともと原点合わせをしているので,連立方程式として解を求めると,原点となる筈です.但し今は解を求めることではなく,それらの方程式に含まれる特性があれば,それは何かを探るのが目的です.
今迄の表現をより簡潔にすれば,(3a)より γ(v)^2=c2*c1/{(c1-v)(c2+v)}>0(6) γ はvの未知関数で,v→0のときγ→1,また空間の等方性よりγ(v)=γ(-v).よって γ(-v)^2=c2*c1/{(c1+v)(c2-v)}>0 (7) (6)(7)を連立させて,c1=c2[=C], -C<v<Cを得る.(証明終)
高校代数レベルで証明しようとしていることの道筋 イ.連立方程式を立てる(1a)(1b) → x,tの同次一次の形 ロ.適当な変数変換をして変数の数を減らす→時空比c1=x1/t1,c2=x2/t2に着目 ハ.簡潔な式に変形→(3a)→(6) ニ.対称条件を適用→(7) ホ.何らかの特性を推論→時空比一定の定理
ニ.の対称条件は(3a)でc1,c2を交換することと同値,即ちc1,c2の,ひいてはS1,S2の対等条件からもホ.を導くことができます(No.19923の方法).
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/21(Wed) 23:30)
(1a), (1b), (2a), (2b)は連立方程式ではないのでしょうか? 連立方程式でないとすれば,No.19954の理論は成り立たないはずですが・・・. 連立方程式だとすれば,その解を求めるのは自然なことだと思います. その結果おかしい解が得られれば,その連立方程式自体がおかしいと考えるのが普通だと思いますが,フジモリさんはそうは考えないで,解を求めるのが適切でないとお考えのようですね. しかし,おかしい解になるからといって解を求めずに議論をしようというのでは,議論が制約されて十分な議論ができないことになると思います.
また,(2a), (2b)を用いずに(3a)→(6)→(7)とするとしても,(6)→(7)とする根拠が不明確です. 対称条件を適用→(7)とされていますが,その対称条件とは,vを-vで置き換えても(またはc1,c2を交換しても)かまわないということのようですね. しかし,その対称条件が成り立つ根拠はどこにあるのでしょうか. No.19976の「S1から見て,S2であるのかS3であるのか区別がつかない」というのが根拠でしょうか? しかしNo.19977で書いたようにS2とS3の区別はつくはずなので,対称条件が成り立つことにはならないと思います.
>S1,S2の対等条件からもホ.を導くことができます(No.19923の方法).
それはできません.No.19925およびNo.19927に書いた通りです.
Re: 相対論 時空比一定の定理
フジモリ さんのレス (2008/05/22(Thu) 07:19)
時空比一定の定理最短版 x2=γ(x1-v*t1)(1a) x1=γ(x2+v*t2)(1b) 見かけ上x,tの同次一次連立方程式であるから,変数変換ci=xi/ti(=時空比)を行いその特性を調べる. (1a)*(1b) c2*c1=γ^2(c1-v)(c2+v)(3a) よってγ(v)^2=c2*c1/{(c1-v)(c2+v)} [=c1*c2/{c1*c2+(c1-c2)v-v*v}](6) γ はvの未知関数で,v→0のときγ→1,また空間の等方性よりγ(v)=γ(-v).(6)でγ(v)^2は偶関数だからvの一次係数は0,よって c1=c2[=±C], -C<v<C, γ(v)=1/√(1-v^2/C^2)を得る. 証明終り
>その結果おかしい解が得られれば →解は原点にあり,おかしくはないと思います.
>対称条件を適用→(7)とされていますが,その対称条件とは,vを-vで置き換えても(またはc1,c2を交換しても)かまわないということのようですね.しかし,その対称条件が成り立つ根拠はどこにあるのでしょうか. →空間の等方性よりγ(v)=γ(-v)です.方向の無区別性といってもいいです.v→0のときγ→1でガリレイ変換とも矛盾しません.この条件こそ従来見過ごされてきた点です.
>>またはc1,c2を交換しても →交換というのは単に逆さ側から見るということではなく,同じ側からみながらc1,c2(S1,S2)を交換するという相対的な交換です.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/22(Thu) 10:03)
>→解は原点にあり,おかしくはないと思います.
c1=c2 すなわち x1/t1=x2/t2 は,原点では 0/0=0/0 という無意味な式になります. 原点でなくても t1=t2=0, x1=x2 であれば解になるようですが,その場合も x1/0=x2/0 という無意味な式になります. これ以外の場合は解にならないので,一般の場合に x1/t1=x2/t2 が成り立つことは証明されません. また,vの値に無関係に γ=1 になるのもおかしいと思います.
>→空間の等方性よりγ(v)=γ(-v)です.方向の無区別性といってもいいです.v→0のときγ→1でガリレイ変換とも矛盾しません.この条件こそ従来見過ごされてきた点です.
見過ごされてはいません.ローレンツ変換を導く過程で用いられています. ところが,(6)→(7)においてこの条件は用いられていません.vを-vで置き換えているだけです. もし(7)が成り立てば γ(v)=γ(-v) の条件を適用して γ(v)^2=c2*c1/{(c1+v)(c2-v)}>0 を導くことができますが,それ以前に(7)が成り立つかどうかが問題です. つまり(6)のvを-vで置き換えた式が成り立つかどうかということですが,No.19977に書いたようにこれは成り立たないと思います.
>→交換というのは単に逆さ側から見るということではなく,同じ側からみながらc1,c2(S1,S2)を交換するという相対的な交換です.
その交換では,交換前と異なる状態になるので,交換前の状態について成り立つ式と交換後の状態について成り立つ式が同時に成り立つことは一般にはありません.
Re: 相対論 時空比一定の定理
フジモリ さんのレス (2008/05/22(Thu) 19:14)
>c1=c2 すなわち x1/t1=x2/t2 は,原点では 0/0=0/0 という無意味な式になります →細かくは申し上げませんでしたが,xi=ci*ti と定義すれば原点を含めて成り立つ関係です.
>原点でなくても t1=t2=0, x1=x2 であれば解になるようですが →原点以外に解はありません.xi=v*tiですから.t1=t2=0であれば,必ずx1=x2=0となります.またγは係数として扱って下さい
>,(6)→(7)においてこの条件は用いられていません.vを-vで置き換えているだけです. →意味が理解できません.γ(v)=γ(-v) の条件よりγ(v)^2=γ(-v)^2となり,(6)→(7)においてvを-vで置き換えるのは正当な処理だと思います.
>見過ごされてはいません.ローレンツ変換を導く過程で用いられています →具体的な式にどうγ(v)=γ(-v)が適用されているのか,数式で提示して下さい.
>その交換では,交換前と異なる状態になるので,交換前の状態について成り立つ式と交換後の状態について成り立つ式が同時に成り立つことはありません →慣性系が対等であるとして,相対性原理の定義より導かれる関係です.
Re: 相対論 時空比一定の定理
MXK さんのレス (2008/05/22(Thu) 22:41)
相変わらずロジックが変ですが,補正しながら考えると,こんな話ではないでしょうか?
系1 (基準系): 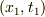 , 系2 (相対速度
, 系2 (相対速度 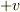 ):
): 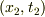 , 系3 (相対速度
, 系3 (相対速度 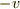 ):
): 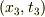 に対して,関係
に対して,関係
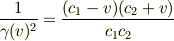
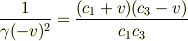
がそれぞれ成り立つ.
ここで, 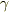 の対称性
の対称性 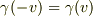 と系2, 3での速度の「同一性」
と系2, 3での速度の「同一性」 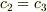 を要求すると,所望の
を要求すると,所望の 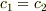 が出ます.
系2で見た場合と系3で見た場合に同じになるような速度
が出ます.
系2で見た場合と系3で見た場合に同じになるような速度 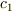 が存在することを要求していることになります.
遠まわしに不変な速度の存在を仮定しているわけです.
が存在することを要求していることになります.
遠まわしに不変な速度の存在を仮定しているわけです.
ローレンツ変換の式の半分 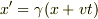 (慣性系毎の時間の違いも考慮) と上のような遠まわしな仮定を
使っているので,有難さは殆どないように思います.
(慣性系毎の時間の違いも考慮) と上のような遠まわしな仮定を
使っているので,有難さは殆どないように思います.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/22(Thu) 22:45)
>→細かくは申し上げませんでしたが,xi=ci*ti と定義すれば原点を含めて成り立つ関係です.
連立方程式(1a), (1b), (2a), (2b)は t1=t2=0 の場合にしか成り立ちません. その場合は xi=ci*0 になりますが,xi=0 ならばciは定まらず,xi≠0 ならば,ciは定義されません.
>→原点以外に解はありません.xi=v*tiですから.t1=t2=0であれば,必ずx1=x2=0となります.またγは係数として扱って下さい
(1a), (1b), (2a), (2b) で t1=t2=0, γ=0 と置くとすべて x1=x2 になります. また,t1=t2=0, γ=0, x1=x2 と置くと (1a), (1b), (2a), (2b) のすべての式が満たされます.従って x1=x2≠0 も解になります.
>→意味が理解できません.γ(v)=γ(-v) の条件よりγ(v)^2=γ(-v)^2となり,(6)→(7)においてvを-vで置き換えるのは正当な処理だと思います.
(6)にγ(v)=γ(-v) の条件を適用すると γ(v)^2=c2*c1/{(c1-v)(c2+v)}>0 になりますが,(7)にはなりません. γ(v)=γ(-v) ということは,γ(v)の中のvを-vに置き換えてもかまわないということですが,γ(v)の外のvまで-vに置き換えてもかまわないということではありません.
>具体的な式にどうγ(v)=γ(-v)が適用されているのか,数式で提示して下さい.
これについては,訂正しておかないといけませんが,多くの場合は光速度不変の原理を適用して直接 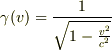 を導いているので結果的にγ(v)=γ(-v) となりますが,導く過程では用いていませんね.
しかし,ローレンツ変換を導く方法はいろいろあって,テルレツキーの「相対性理論のパラドックス」では,空間の対称性からγ(v)=γ(-v) を導き,それによって
を導いているので結果的にγ(v)=γ(-v) となりますが,導く過程では用いていませんね.
しかし,ローレンツ変換を導く方法はいろいろあって,テルレツキーの「相対性理論のパラドックス」では,空間の対称性からγ(v)=γ(-v) を導き,それによって 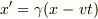 と
と 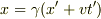 という関係式が成り立つとしています.(γのかわりにκという文字を用いていますが内容的には同じです.)
という関係式が成り立つとしています.(γのかわりにκという文字を用いていますが内容的には同じです.)
>→慣性系が対等であるとして,相対性原理の定義より導かれる関係です.
慣性系が対等であることがすなわち相対性原理だと思いますが,それによって交換前について成り立つ式と交換後に成り立つ式が同時に成り立つことは導けません. 相対性原理はそんなことは主張していません.
MXKさんのように考えれば,フジモリさんの主張とはちょっとずれますが辻褄は合いますね. すべての座標系に共通な不変速度の存在を仮定しないで,2つの座標系で不変な速度があればそれ以外の座標系でも不変になることを示せるという点では意味があるかもしれないとも思いましたが,光速度不変の原理を用いてローレンツ変換を導く場合も,普通は2つの座標系で光速が等しくなることしか利用していないので実質的には同じことかも・・・.
Re: 相対論 時空比一定の定理
フジモリ さんのレス (2008/05/23(Fri) 12:04)
漸く本筋で合意ができたと嬉しく思います.活発な議論有難うございました.
>(1a), (1b), (2a), (2b) で t1=t2=0, γ=0 と置くとすべて x1=x2 になります. →t1=t2=0のときx1^2=x2^2となりますが,他の条件よりx1=x2=0となります.γは係数として消去はかまいませんがあえて変数としての解を求めることの意味が分りません.連立方程式の解は原点のみですが,このことと時空比一定の性質とは両立する関係です.
>γ(v)=γ(-v) ということは,γ(v)の中のvを-vに置き換えてもかまわないということですが,γ(v)の外のvまで-vに置き換えてもかまわないということではありません. →よい点をご指摘戴きました.論理を改めます.
>有難さは殆どないように思います →有難さとは何を意味するのか分りませんが,確かにローレンツ変換以後の世界が変わる訳ではないです.しかし光速度不変の原理が相対性原理から導かれる時空比一定の定理に吸収され,相対性原理の枠組みがすっきりすると思います.光速度不変が相対的必然性からきているとは,少々驚きました.
今迄の議論を改訂版の形にまとめて,来週別議題で投稿します. 英語物理掲示板の紹介も受けたので,そちらにも投稿する予定です.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/23(Fri) 14:38)
>→t1=t2=0のときx1^2=x2^2となりますが,他の条件よりx1=x2=0となります.γは係数として消去はかまいませんがあえて変数としての解を求めることの意味が分りません.連立方程式の解は原点のみですが,このことと時空比一定の性質とは両立する関係です.
他の条件とは何か分かりませんが,連立方程式だけからは x1=x2=0 は導けません.仮に x1=x2=0 しか解がないとすると,x1=x2=0 以外の場合には連立方程式自体が成り立たないことになります.従って x1=x2=0 以外の場合にどうなるかは,連立方程式からは何も導けません. また,この場合には時空比一定の定理とも両立しません.両立するということは連立方程式と時空比一定の定理の両方ともが成り立つことができるということですが,両方どころか片方(連立方程式)さえも成り立たないからです.
>→有難さとは何を意味するのか分りませんが,確かにローレンツ変換以後の世界が変わる訳ではないです.しかし光速度不変の原理が相対性原理から導かれる時空比一定の定理に吸収され,相対性原理の枠組みがすっきりすると思います.光速度不変が相対的必然性からきているとは,少々驚きました.
MXKさんのように考えれば c1=c2 が導けますが,その場合は相対性原理の他に c2=c3 を仮定しています.この仮定なしに相対性原理だけからc1=c2 が導かれるわけではありません. c2=c3 という仮定は,2つの慣性系に共通な不変速度があることを意味していて光速度不変の原理を少し弱めたものです.つまり,すべての慣性系に共通な不変速度(光速度)の存在を,2つの慣性系に共通な不変速度の存在に弱めているわけです. しかし,ローレンツ変換の普通の導き方でも,光速度不変の原理は弱められた形でしか用いられていないので,フジモリさんの理論(をMXKさんが修正したもの)が特に新しい内容を含んでいるようには思えません. 光速度不変の原理と実質的に同じものを,名前を聞いただけでは内容の分かりにくい「時空比一定の定理」と呼ぶのも疑問です.
Re: 相対論 時空比一定の定理
MXK さんのレス (2008/05/23(Fri) 15:32)
合意できているとはとても思えませんが...
そもそもフジモリさんの議論は,基本的なレベルでの矛盾が多いことは,他の方々が指摘されている通りです.特に,No.19962 のアドバイスは適切です.
他者による善意的拡大解釈を経て,何とか既存の理論に収まることが確認できただけです. その結果分かったことは,「遠まわしに不変速度の存在を仮定して,不変速度の存在が証明できた」ということに他ならないということです.
 ,
, 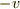 での速度の同一性を要求するぐらいなら,
での速度の同一性を要求するぐらいなら,  ,
,  での速度の同一性,すなわち,
での速度の同一性,すなわち, 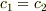 を仮定する方が直裁で, 物理的にもずっと分かりやすいです.
これは通常,光速不変の原理(不変速度の存在)と呼ばれているものです.
を仮定する方が直裁で, 物理的にもずっと分かりやすいです.
これは通常,光速不変の原理(不変速度の存在)と呼ばれているものです.
Re: 相対論 時空比一定の定理
yama さんのレス (2008/05/23(Fri) 23:29)
よく考えてみると,c2=c3を仮定してc1=c2が導けたとしてもそれだけではまだ不変速度の存在の証明としては不十分であるように思われます. というのはこれらが共通の値を持つとしてもそれが定数であることが証明されていないからです.つまり共通の値が速度vの関数になる可能性が排除できないからです.その場合,別の任意の慣性系S4で測定したc4が同じ値になることも保証されません.S1はS2,S3と特別な関係(S1から見てS2とS3が逆向きに同じ速さで動くという関係)にありますが,S4とS2,S3の間にはそのような特別な関係がないからです.
c2=c3の値が速度に無関係な定数になると仮定すれは,c1もc4もこの定数に等しくなることは容易に分かりますが,この仮定は不変速度の存在そのものであるといってよいでしょう.