フジモリ さんの書込 (2008/05/13(Tue) 08:33)

初めまして，藤森弘章と申します．親父の権威を示そうと大学生の愚女に相対論のさわりを吹聴していて脱線，その昔落ちこぼれた積ん読の書を紐解くうちに，美しい公式が微笑みました．二番煎じでなければ新公式として，この場をお借りして発表します．本サイトの相対論の記述にご利用下さい．

新公式 x軸方向に運動するn個の慣性座標系 1,2,...,n があり，それらの相対速度は v1,v2,...,vn である．viは慣性系 i から見た慣性系 i+1 の速度であり，vnは慣性系 n から見た慣性系 1 の速度である．このとき v1,v2,...,vnの関係は，光速を c として (c-v1)(c-v2)・・・(c-vn) ＝ (c+v1)(c+v2)・・・(c+vn) である．n=3 の場合，アインシュタインの速度合成則を得る．

• 本公式が既出であれば，その文献をメールにて私までお知らせ下さい．
• 証明はいくつかありますが，次回載せます．
• プロジェクト・メンバーのご賛同があれば，新公式を「かぎしっぽの公式」と命名したいと思います．

toorisugari no Hiro さんのレス (2008/05/13(Tue) 14:11)

初めましてフジモリさま

初めて見るきれいな式だと思います．

ですが，この式は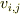， を系iから観測した系jの相対速度として，通常の速度合成則

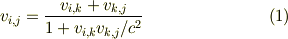
と同値な式

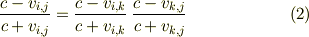
から自明に導かれる式

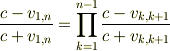
において 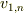を 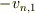にしたものにすぎません．

また，この式が意味するところがわからないので「公式」と呼べないと思います．

# (1)あるいはおまけして(2)は公式と呼んでよいと思いますが．．．そもそも(1)は 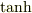の合成則ですから，(2)に進むより，ローレンツブースト 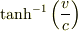の加法則に進んだ(戻った)方が自然ですね．

ただし，この段階ではこの「公式」は単なる式にすぎませんが，もし，自明でない現象がこの式を使って初めて簡単に理解できるのなら，あるいは自明でない有意味で有用な理論が初めて導き出せるのなら，公式として名前がつくと思います．

フジモリ さんのレス (2008/05/13(Tue) 23:04)

toorisugari no Hiroさん，卓見です．証明の一つを説明する手間が省けました．なお小生は市井の一親爺に過ぎませんので，フジモリ「さん」と呼んで下さい．

新公式証明その2 単純化のため直線上を相対速度vで等速運動している慣性座標系S1(x1,t1),S2(x2,t2)を考え，それぞれのx軸の正方向を同じ方向にとり，原点を一致させる． S1(x1座標)から見たS2の原点(x2=0)の運動は x1=v*t1 であるから，x2は因数 (x1-v*t1) をもつ．よって x2=γ(x1-v*t1)(1a)但し γ はvの未知関数 同様に x1=γ(x2+v*t2)(1b)ここまでは教科書通り

n個の慣性座標系の関係 1,2,...,nの慣性座標系があり，それぞれのx軸の正方向を同じ方向にとり，原点を一致させる．慣性系の相対速度を v1,v2,...,vn とする．viは慣性系 i から見た慣性系 i+1 の速度であり，vnは慣性系 n から見た慣性系 1 の速度である． (1a)(1b)の関係を1,2,...,nまで記述する．j=i+1,i=nのときj=1とするとi=1〜nで xj=γi(xi-vi*ti) (1ai) xi=γi(xj+vi*tj) (1bi) (1ai)(1bi)でiを1〜nまでそれぞれ両辺を掛け合わせて比べる． [Πxj=Πxi=] Πγi*ti(xi/ti-vi)=Πγi*tj(xj/tj+vi)(2) 光速度不変の原理より光速をCとして， xi/ti=C であるから Πγi*ti(C-vi)=Πγi*tj(C+vi) (3) ここでΠγi*ti=Πγi*tjを消去すると新公式(4)を得る．

(C-v1)(C-v2)・・・(C-vn) ＝ (C+v1)(C+v2)・・・(C+vn) (4)

>あるいは自明でない有意味で有用な理論が導き出せるのなら，公式として名前がつくと思います． ローレンツ変換を経由せずに得られる新公式の過程で，ある奇妙なことに気付きました．[続く]

フジモリ さんのレス (2008/05/14(Wed) 07:38)

「ある奇妙なこと」とは，(2)より導かれる式 Π(xi/ti-vi)=Π(xj/tj+vi)(5) のことです．ここで系iと系jは対等ですから，乱暴に考えればxi/tiとxj/tjを入換えても成り立つはずです． Π(xj/tj-vi)=Π(xi/ti+vi)(6) これ即ち xi/ti=xj/tj を示唆しているのではないかと考えました．二個の慣性系の基本に立ち返って考え直した結論を以下に示します．

1.時空比一定の定理 式の番号はリセットしますが，式(1a)(1b)までは，前回投稿の「新公式証明その2」と同一のため省略

(1a)(1b)は見かけ上x,tの同次一次方程式であるが，その特性を調べる． 両辺を掛け合わせて x2*x1=γ^2(x1-v*t1)(x2+v*t2)(2) (2)の両辺をt1*t2で割ると x2/t2*x1/t1=γ^2(x1/t1-v)(x2/t2+v)(3) ここで時空比を ci=xi/ti (i=1,2) と定義すると(3)は c2*c1=γ^2(c1-v)(c2+v)(4a) S1,S2は対等だから(4a)で c1⇔c2 としても(又は相対速度を v→-v としても) 成り立つ．又は(4a)でγ(v)=γ(-v)と考えてもよい． c1*c2=γ^2(c2-v)(c1+v)(4b) (4a)(4b)を連立して (c1-v)(c2+v)=(c1+v)(c2-v), v(c1-c2)=0 (5) 結局c1=c2=x1/t1=x2/t2[=C]となる．即ち両慣性座標系の時空比は等しい． (4a)は時空比Cを用いて C^2/γ^2=(C-v)(C+v) >=0 (6) よって-C<=v=<C を得る． また(6)より γ=1/√(1-v^2/C^2) >=1(7) 以上より対等な慣性座標系の特性として，時空比一定の定理を得る．

時空比一定の定理 −全ての慣性座標系の時空比は共通値Cをもつ．原点(xi=ti=0)を合わせたとき C=xi/ti 即ち時間は空間に比例した量であり，その比は全ての慣性系で共通一定値である． −相対速度vは時空比C を超えない．即ち-C<=v=<C −γの値はv/Cの関数として求まる．即ちvはCで規格化される． [もう一回続く]

フジモリ さんのレス (2008/05/14(Wed) 08:27)

2.ローレンツ変換 時空比一定の定理より(1a)でx=C*tまたはt=x/Cに置き換えると C*t2=γ(C*t1-v/C*x1)(1a') (1a)(1a')の組で(x1,t1)→(x2,t2)の座標変換公式を得るが，これはローレンツ変換である．

3.n個の慣性座標系の関係 1,2,...,nの慣性座標系があり，それぞれのx軸の正方向を同じ方向にとり，原点を一致させる．慣性系の相対速度を v1,v2,...,vn とする．viは慣性系 i から見た慣性系 i+1 の速度であり，vnは慣性系 n から見た慣性系 1 の速度である． (1a)(1b)の関係を1,2,...,nまで記述する．j=i+1,i=nのときj=1とするとi=1〜nで xj=γi(xi-vi*ti) (1ai) xi=γi(xj+vi*tj) (1bi) (1ai)(1bi)でi=1〜nまで両辺を掛け合わせて比べる．慣性系の時空比は一定 xi/ti=C だから [Πxi=ΠC*ti=] Πγi*ti(C-vi)=Πγi*tj(C+vi) (8) ここでΠγi*tiを消去すると新公式(9)を得る． (C-v1)(C-v2)・・・(C-vn) ＝ (C+v1)(C+v2)・・・(C+vn) (9)

この式の物理的含意を吟味してみる． イ.-C<vi<C (i=1〜n-1)のとき-C<vn<C→相対速度vは時空比を超えて存在できない． ロ.v1=C のとき，その他のn-1個の相対速度のうち少なくとも一つはvi=-Cであり，他は定まらないので，相対速度v=±Cの慣性系を慣性系群に含めるのは不適切である． ハ.n=3(慣性系S1,S2,S3)の場合，v1=u,v2=-u のとき v3=0でS1とS3は一致するが，v1=C,v2=-C のとき v3=不定，となり一般にS1とS3は一致しない． → 相対速度が意味をもつためには，相対速度¬=±Cという制約がある． ニ.Cを-Cに置き換えても(9)は不変である．即ち(x,t)の第2,4象限における時空比=-C． ホ.二つの慣性系の相対速度vが互いに等しいことを自然はどう保証するのか．共通時空比Cの存在はその必要十分条件を満たしている．

4.時空比と物理定数の関係 フィゾーの光と流体の合成速度実験，マイケルソン-モーレーの実験の結果を見るに，時空比Cは真空中の光速cで代表するのが妥当である．即ち，時空比C=光速c ．これは全ての慣性系で光速cは等しいことと一致する．光速cは重力・素粒子に働く力など，作用の伝播速度に等しいと推定される． (9)でn=3 の場合，慣性系の速度合成則を得る．

アインシュタインがアッカンベーをしそうですが，光速度不変の原理の居場所がありません．こんなことってあるんでしょうか．どこかに間違いがあればご指摘下さい．

yama さんのレス (2008/05/14(Wed) 11:53)

フジモリさん，はじめまして 細かいところまでは見ていませんが

>c2*c1=γ^2(c1-v)(c2+v)(4a) から >c1*c2=γ^2(c2-v)(c1+v)(4b) が導かれるという点に疑問があります．

>S1,S2は対等だから(4a)で c1⇔c2 としても(又は相対速度を v→-v としても) 成り立つ．

と説明されていますが，これは成り立たないと思います． c1⇔c2 とするならば，同時にv→-vとしなければならないはずであり，その場合には同じ式が得られるだけです．

また，そもそも(x1,t1)が何を意味するのかよくわかりません． 座標変換を考えるのなら，(x1,t1)を任意の座標としないと意味がありません． (x1,t1)をt=0で原点から出る光の座標とすれば x1/t1=x2/t2 が成り立つと思いますが，(x1,t1)を任意の座標とする場合には x1/t1=x2/t2 は一般には成り立たないと思います．

フジモリ さんのレス (2008/05/14(Wed) 17:41)

そうです，yamaさん，ここ(4b)がキーポイントです． 独立に考えてS1,S2の相対速度が -v の時，(1a)(1b)の式でv→-vと修正，(2)(3)と同様に変形して(4b)の関係が成り立つこと迄は納得されると思います．問題は(4a)(4b)を連立式として扱ってよいかどうかです．c1,c2,vという変数で見た場合，vの拘束条件／対称性をみるため，連立することに意味があると考えました．

>(x1,t1)を任意の座標とする場合には x1/t1=x2/t2 は一般には成り立たないと思います． x1/t1=x2/t2=C(一定値)は成り立つという主旨です．ある慣性座標系で時空比cが定まれば他の座標系でも同じ時空比をとるという意味です．c(=x/t)は原点を通るxt座標の直線の傾きを表わす変数です．

yama さんのレス (2008/05/14(Wed) 18:46)

(4a)から(4b)は導けないということです． (4a)でc1⇔c2 とすると同時にv→-vとすると，もとの(4a)になるだけで(4b)にはなりません． また，(1a)(1b)の式でv→-vとしたものは，相対速度の向きが逆になるため(1a)(1b)と同時には成り立ちません．

ところで，x1/t1=x2/t2=C(一定値)の場合の(x1,t1)とは何でしょうか． (x1,t1)が何を示すのか分からなければ，その比が一定というのも意味が分からないことになります． また，原点を通る直線の傾きが，２つの座標系で等しくなることも一般には成り立たないと思います． （その直線が光の経路を表す場合には成り立つと思いますが・・・．）

フジモリ さんのレス (2008/05/14(Wed) 22:53)

話を「特殊相対論の新公式発見」にもどして， toorisugari no HiroさんのNo.19918の件ですが，速度合成則はおしなべてローレンツ変換を経由した出自であるのに対し，本公式はNo.19922で示したように同変換とは無関係に導いたものであり，しかも速度合成の一般則が直接導出されることから，本公式を「公式」と名乗ってもおかしくはないと思います．当然一方が他方を導くことのできる同値関係ではありますが．いかがでしょうか．

ミュフ猫 さんのレス (2008/05/15(Thu) 00:23)

>速度合成則はおしなべてローレンツ変換を経由した出自であるのに対し， >本公式はNo.19922で示したように同変換とは無関係に導いたものであり・・・

と仰られてますが，そのNo.19922の導出方法に，

>光速度不変の原理より光速をCとして， xi/ti=C であるから・・・

とか，しっかり間接的にローレンツ変換を使ってるような．ｗ そもそも，ローレンツ変換自体が光速度不変の原理の産物でしょうに．ｗ ついでに，「時間」と「位置」の座標変換式がローレンツ変換であり， 「速度」の座標変換式が速度合成則なわけで，どちらも出所は， 光速度不変の原理かと・・・．

yama さんのレス (2008/05/15(Thu) 00:37)

公式と呼ばれるかどうかは，その有用性に関係しますが，導き方にはあまり関係しないと思います． ただし，新しい導き方によって適用範囲が広がれば，有用性が増すことはあると思います． たとえば，特殊な条件を仮定して導かれた式は，その条件が成り立つ場合にしか適用できません．しかし，その条件を仮定せずに同じ式を導くことができたとすれば，その条件が成り立たない一般の場合にも適用できることになるので有用性が増すでしょう．

今回の式については，ローレンツ変換を利用していないとしても，ローレンツ変換の基になった相対性原理と光速度不変の原理を用いているわけですから，ローレンツ変換を用いたのと実質的には同等であり，適用範囲も変わりません．

toorisugari no Hiro さんのレス (2008/05/15(Thu) 12:23)

今回の一連の フジモリさん の記事は「公式」発見というより，「演習問題」発見か「説明法(解法)」発見というレベルでしかないと思います．しかも，新しくもないし，問題によっては間違っています．理由は私やyamaさんが既にふれていることですから繰り返すのはやめます．

特殊相対論は量子論がからまないかぎり数学的構造がはっきりわかっています．少なくとも学部レベルで扱える数学的枠組みの中では新しい「公式」などは出ません．(出ても間違いか自明か無意味なだけです．)

ただし，既知の公式や理論から自明に導きだせるにすぎない式でも「公式」と呼ばれることもあり得ます．有用性が明らかになったときです．

現象を上手に説明できるといった例を出したましたが，ほかには，例えば，「計算機で相対論的現象を計算する場合，この式で計算した方が，数値誤差が少ない，計算時間が短い」といった「新しい有用な技術」と結びつく場合です．

でも，この場合でも，この「公式の発見者」の名は技術を開発した研究者(有用性の発見者)に帰せられるのであり，導出しただけの人が並び称されることはありません．

MXK さんのレス (2008/05/15(Thu) 23:30)

綺麗な式ですね．

この式は 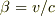を用いると，

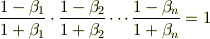
となります． さらに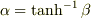， を用いると，

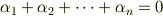
と書き直すことができます． これは, 個のローレンツ変換の合成が恒等変換となるということです．

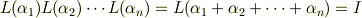
ここで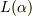， は以下で定義されるローレンツ変換です．

速度合成の公式の特別な場合にすぎないので，残念ながら，特に新しいということはなさそうです．