電磁気（アンペールの式について）

電磁気（アンペールの式について）

Mickey さんの書込 (2008/05/11(Sun) 23:10)

初めてこちらに記載させていただきます． よろしく御願いします．基本的な疑問なのですが

マクスウェルの方程式で一般的に第二式となっているもので， 電流は，積分形で 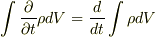\int\frac{\partial}{\partial t}\rho dV=\frac{d}{dt}\int \rho dV （全微分）となり 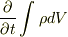\frac{\partial}{\partial t}\int \rho dV （偏微分）ではないらしいのですが， いまいちこの（時間）微分の意味するところが不明です （教科書でもとくに表記が統一されていません）．

個人的には，時間は位置と独立な変数と考え（むしろ全てに影響するので），相対論的に考える以外は，全微分で良いと思うのですが，

実際は，全微分？偏微分？どちらなのでしょうか． さらに，積分から微分を出す際 C^2 級で全微分へと変わるようですが そのあたり （ C^2 級だからなのか，積分を出す際に何か条件や操作［操作］があるのか） がよく分かりません．

Refs. [1]ランダウほか「 場の理論」 東京図書出版 [2]加藤正昭 「電磁気学」 東京大学出版会 [3]山田直平ほか 「電気磁気学(電気学会大学講座)」 オーム社 [4]日本数学学会 「数学辞典」 岩波書店

Re: 電磁気（アンペールの式について）

yama さんのレス (2008/05/11(Sun) 23:37)

\rho は (x,y,z,t) の関数なので，ある一定の位置での \rho の時間的変化率は偏微分を用いて \frac{\partial\rho}{\partial t} で表されます．

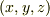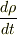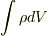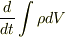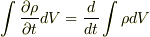位置 (x,y,z) が時間的に変化していて，その位置での \rho の時間的変化率を考える場合は全微分を用いて \frac{d\rho}{dt} で表わします． これに対して定積分 \int\rho dV は t だけの関数なので，その時間的変化率は常微分を用いて \frac{d}{dt}\int\rho dV で表されます． （公式 \int\frac{\partial\rho}{\partial t}dV=\frac{d}{dt}\int\rho dV の積分は定積分であって不定積分ではないことに注意してください．）